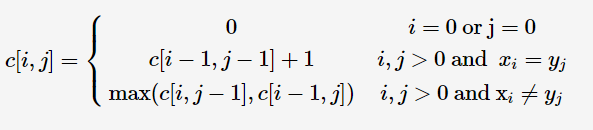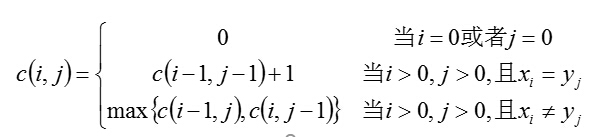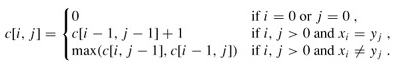1. 问题描述

子串应该比较好理解，至于什么是子序列，这里给出一个例子：有两个母串

cnblogs
belong

比如序列bo, bg, lg在母串cnblogs与belong中都出现过并且出现顺序与母串保持一致，我们将其称为公共子序列。最长公共子序列（Longest Common Subsequence, LCS ），顾名思义，是指在所有的子序列中最长的那一个。子串是要求更严格的一种子序列，要求在母串中连续地出现。在上述例子的中，最长公共子序列为blog（cn blog s, b e lo n g ），最长公共子串为lo（cnb lo gs, be lo ng）。

2. 求解算法

对于母串X=<x1,x2,⋯,xm>, Y=<y1,y2,⋯,yn>，求LCS与最长公共子串。
暴力解法
假设 m<n，对于母串X，我们可以暴力找出2的m次方个子序列，然后依次在母串Y中匹配，算法的时间复杂度会达到指数级O(n∗2的m次)。显然，暴力求解不太适用于此类问题。
动态规划
假设Z=<z1,z2,⋯,zk>是X与Y的LCS，我们观察到
如果Xm=Yn，则Zk=Xm=Yn，有Zk−1是Xm−1与Yn−1的LCS；
如果Xm≠Yn，则Zk是Xm与Yn−1的LCS，或者是Xm−1与Yn的LCS。
因此，求解LCS的问题则变成递归求解的两个子问题。但是，上述的递归求解的办法中，重复的子问题多，效率低下。改进的办法——用空间换时间，用数组保存中间状态，方便后面的计算。这就是动态规划（DP)的核心思想了。
DP求解LCS
用二维数组c[i][j]记录串x1x2⋯xi与y1y2⋯yj的LCS长度，则可得到状态转移方程

由最长公共子序列问题的最优子结构性质可知，要找出X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的最长公共子序列，可按以下方式递归地进行：当x_m=y_n时，找出X_m-1和Y_n-1的最长公共子序列，然后在其尾部加上x_m(=y_n)即可得X和Y的一个最长公共子序列。当x_m≠y_n时，必须解两个子问题，即找出X_m-1和Y的一个最长公共子序列及X和Y_n-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。

在算法LCS中，每一次的递归调用使i或j减1，因此算法的计算时间为O(m+n)。

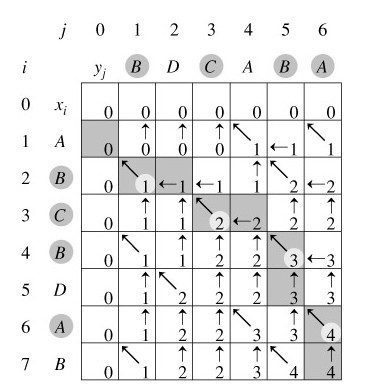
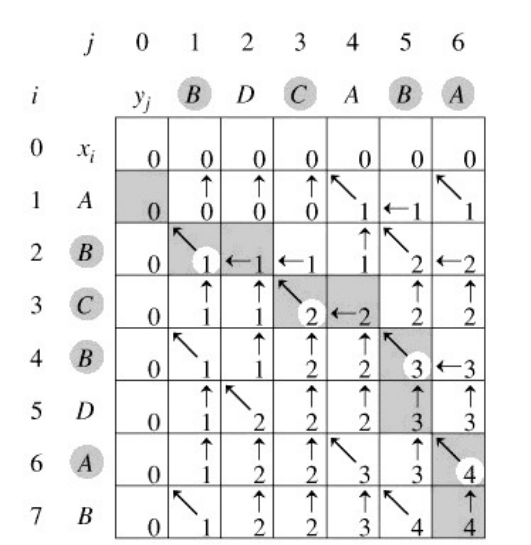
例如，设所给的两个序列为X=<A，B，C，B，D，A，B>和Y=<B，D，C，A，B，A>。由算法LCS_LENGTH和LCS计算出的结果如下图所示：

代码实现

[cpp]  view plain copy  
 print ? 
 public static int lcs(String str1, String str2) {  
     int len1 = str1.length();  
     int len2 = str2.length();  
     int c[][] = new int[len1+1][len2+1];  
     for (int i = 0; i <= len1; i++) {  
         for( int j = 0; j <= len2; j++) {  
             if(i == 0 || j == 0) {  
                 c[i][j] = 0;  
             } else if (str1.charAt(i-1) == str2.charAt(j-1)) {  
                 c[i][j] = c[i-1][j-1] + 1;  
             } else {  
                 c[i][j] = max(c[i - 1][j], c[i][j - 1]);  
             }  
         }  
     }  
     return c[len1][len2];  
 }  

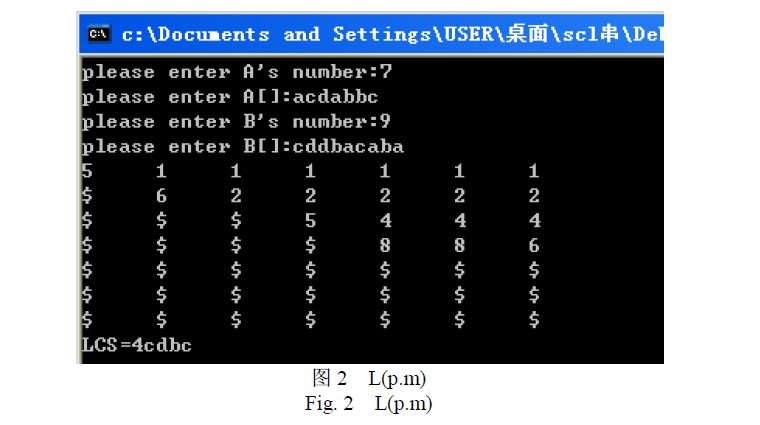
DP求解最长公共子串

前面提到了子串是一种特殊的子序列，因此同样可以用DP来解决。定义数组的存储含义对于后面推导转移方程显得尤为重要，糟糕的数组定义会导致异常繁杂的转移方程。考虑到子串的连续性，将二维数组c[i][j]用来记录具有这样特点的子串——结尾同时也为为串x1x2⋯xi与y1y2⋯yj的结尾——的长度。
得到转移方程：

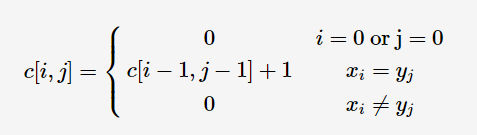
最长公共子串的长度为 max(c[i,j]), i∈{1,⋯,m},j∈{1,⋯,n}。
代码实现

[cpp]  view plain copy  
 print ? 
 public static int lcs(String str1, String str2) {  
     int len1 = str1.length();  
     int len2 = str2.length();  
     int result = 0;     //记录最长公共子串长度  
     int c[][] = new int[len1+1][len2+1];  
     for (int i = 0; i <= len1; i++) {  
         for( int j = 0; j <= len2; j++) {  
             if(i == 0 || j == 0) {  
                 c[i][j] = 0;  
             } else if (str1.charAt(i-1) == str2.charAt(j-1)) {  
                 c[i][j] = c[i-1][j-1] + 1;  
                 result = max(c[i][j], result);  
             } else {  
                 c[i][j] = 0;  
             }  
         }  
     }  
     return result;  
 }  