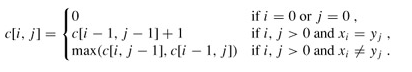程序员编程艺术系列重新开始创作了（前十章，请参考程序员编程艺术第一~十章集锦与总结）。回顾之前的前十章，有些代码是值得商榷的，因当时的代码只顾阐述算法的原理或思想，所以，很多的与代码规范相关的问题都未能做到完美。日后，会着力修缮之。

    搜遍网上，讲解这个LCS问题的文章不计其数，但大多给读者一种并不友好的感觉，稍感晦涩，且代码也不够清晰。本文力图避免此些情况。力保通俗，阐述详尽。同时，经典算法研究系列的第三章（三、dynamic programming）也论述了此LCS问题。有任何问题，欢迎不吝赐教。

    什么是最长公共子序列呢?好比一个数列 S，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。

    举个例子，如：有两条随机序列，如 1 3 4 5 5 ，and 2 4 5 5 7 6，则它们的最长公共子序列便是：4 5 5。

    注意最长公共子串（Longest CommonSubstring）和最长公共子序列（LongestCommon Subsequence, LCS）的区别：子串（Substring）是串的一个连续的部分，子序列（Subsequence）则是从不改变序列的顺序，而从序列中去掉任意的元素而获得的新序列；更简略地说，前者（子串）的字符的位置必须连续，后者（子序列LCS）则不必。比如字符串acdfg同akdfc的最长公共子串为df，而他们的最长公共子序列是adf。LCS可以使用动态规划法解决。下文具体描述。

    解最长公共子序列问题时最容易想到的算法是穷举搜索法，即对X的每一个子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列，并且在检查过程中选出最长的公共子序列。X和Y的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列，因此，X共有2^m个不同子序列（Y亦如此，如为2^n），从而穷举搜索法需要指数时间（2^m * 2^n）。

• 动态规划算法

    事实上，最长公共子序列问题也有最优子结构性质。

记:

Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

• 若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。

• 若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

    由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

    也就是说，解决这个LCS问题，你要求三个方面的东西：1、LCS（Xm-1，Yn-1）+1；2、LCS（Xm-1，Y），LCS（X，Yn-1）；3、max{LCS（Xm-1，Y），LCS（X，Yn-1）}。

    行文至此，其实对这个LCS的动态规划解法已叙述殆尽，不过，为了成书的某种必要性，下面，我试着再多加详细阐述这个问题。

3.1、最长公共子序列的结构

    最长公共子序列的结构有如下表示：

    设序列X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的一个最长公共子序列Z=<z₁, z₂, …, z_k>，则：

1. 若x_m=y_n，则z_k=x_m=y_n且Z_k-1是X_m-1和Y_n-1的最长公共子序列；
2. 若x_m≠y_n且z_k≠x_{m ，}则Z是X_m-1和Y的最长公共子序列；
3. 若x_m≠y_n且z_k≠y_n ，则Z是X和Y_n-1的最长公共子序列。

    其中X_m-1=<x₁, x₂, …, x_m-1>，Y_n-1=<y₁, y₂, …, y_n-1>，Z_k-1=<z₁, z₂, …, z_k-1>。

    由最长公共子序列问题的最优子结构性质可知，要找出X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的最长公共子序列，可按以下方式递归地进行：当x_m=y_n时，找出X_m-1和Y_n-1的最长公共子序列，然后在其尾部加上x_m(=y_n)即可得X和Y的一个最长公共子序列。当x_m≠y_n时，必须解两个子问题，即找出X_m-1和Y的一个最长公共子序列及X和Y_n-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。

    由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算X和Y的最长公共子序列时，可能要计算出X和Y_n-1及X_m-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算X_m-1和Y_n-1的最长公共子序列。

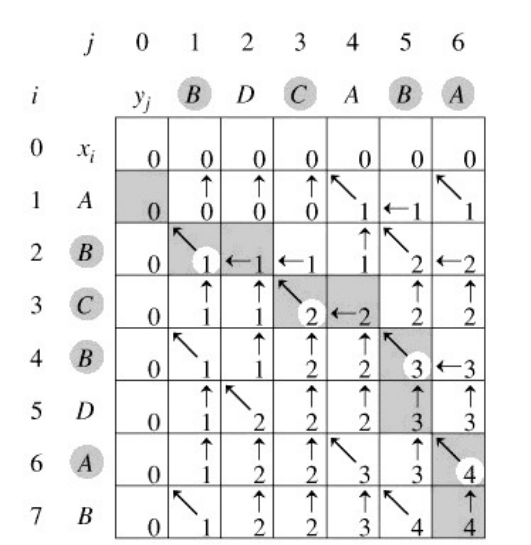
    与矩阵连乘积最优计算次序问题类似，我们来建立子问题的最优值的递归关系。用c[i,j]记录序列X_i和Y_j的最长公共子序列的长度。其中X_i=<x₁, x₂, …, x_i>，Y_j=<y₁, y₂, …, y_j>。当i=0或j=0时，空序列是X_i和Y_j的最长公共子序列，故c[i,j]=0。其他情况下，由定理可建立递归关系如下：

    直接利用上节节末的递归式，我们将很容易就能写出一个计算c[i,j]的递归算法，但其计算时间是随输入长度指数增长的。由于在所考虑的子问题空间中，总共只有θ(m*n)个不同的子问题，因此，用动态规划算法自底向上地计算最优值能提高算法的效率。

    计算最长公共子序列长度的动态规划算法LCS_LENGTH(X,Y)以序列X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>作为输入。输出两个数组c[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储X_i与Y_j的最长公共子序列的长度，b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的，这在构造最长公共子序列时要用到。最后，X和Y的最长公共子序列的长度记录于c[m,n]中。

    由算法LCS_LENGTH计算得到的数组b可用于快速构造序列X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的最长公共子序列。首先从b[m,n]开始，沿着其中的箭头所指的方向在数组b中搜索。

• 当b[i,j]中遇到"↖"时（意味着xi=yi是LCS的一个元素），表示X_i与Y_j的最长公共子序列是由X_i-1与Y_j-1的最长公共子序列在尾部加上x_i得到的子序列；
• 当b[i,j]中遇到"↑"时，表示X_i与Y_j的最长公共子序列和X_i-1与Y_j的最长公共子序列相同；
• 当b[i,j]中遇到"←"时，表示X_i与Y_j的最长公共子序列和X_i与Y_j-1的最长公共子序列相同。

    这种方法是按照反序来找LCS的每一个元素的。由于每个数组单元的计算耗费Ο(1)时间，算法LCS_LENGTH耗时Ο(mn)。

    下面的算法LCS(b,X,i,j)实现根据b的内容打印出X_i与Y_j的最长公共子序列。通过算法的调用LCS(b,X,length[X],length[Y])，便可打印出序列X和Y的最长公共子序列。

在算法LCS中，每一次的递归调用使i或j减1，因此算法的计算时间为O(m+n)。

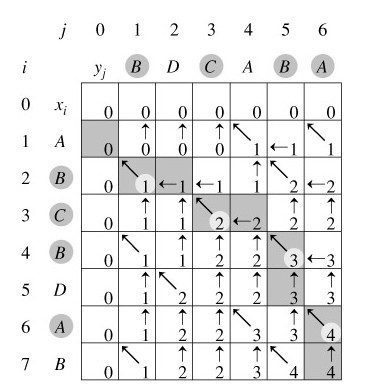
例如，设所给的两个序列为X=<A，B，C，B，D，A，B>和Y=<B，D，C，A，B，A>。由算法LCS_LENGTH和LCS计算出的结果如下图所示：

    我来说明下此图（参考算法导论）。在序列X={A，B，C，B，D，A，B}和 Y={B，D，C，A，B，A}上，由LCS_LENGTH计算出的表c和b。第i行和第j列中的方块包含了c[i，j]的值以及指向b[i，j]的箭头。在c[7,6]的项4，表的右下角为X和Y的一个LCS<B，C，B，A>的长度。对于i，j>0，项c[i，j]仅依赖于是否有xi=yi，及项c[i-1，j]和c[i，j-1]的值，这几个项都在c[i，j]之前计算。为了重构一个LCS的元素，从右下角开始跟踪b[i，j]的箭头即可，这条路径标示为阴影，这条路径上的每一个“↖”对应于一个使xi=yi为一个LCS的成员的项（高亮标示）。

    所以根据上述图所示的结果，程序将最终输出：“B C B A”。

    对于一个具体问题，按照一般的算法设计策略设计出的算法，往往在算法的时间和空间需求上还可以改进。这种改进，通常是利用具体问题的一些特殊性。

    例如，在算法LCS_LENGTH和LCS中，可进一步将数组b省去。事实上，数组元素c[i,j]的值仅由c[i-1,j-1]，c[i-1,j]和c[i,j-1]三个值之一确定，而数组元素b[i,j]也只是用来指示c[i,j]究竟由哪个值确定。因此，在算法LCS中，我们可以不借助于数组b而借助于数组c本身临时判断c[i,j]的值是由c[i-1,j-1]，c[i-1,j]和c[i,j-1]中哪一个数值元素所确定，代价是Ο(1)时间。既然b对于算法LCS不是必要的，那么算法LCS_LENGTH便不必保存它。这一来，可节省θ(mn)的空间，而LCS_LENGTH和LCS所需要的时间分别仍然是Ο(mn)和Ο(m+n)。不过，由于数组c仍需要Ο(mn)的空间，因此这里所作的改进，只是在空间复杂性的常数因子上的改进。

    另外，如果只需要计算最长公共子序列的长度，则算法的空间需求还可大大减少。事实上，在计算c[i,j]时，只用到数组c的第i行和第i-1行。因此，只要用2行的数组空间就可以计算出最长公共子序列的长度。更进一步的分析还可将空间需求减至min(m, n)。

    动态规划的一个计算最长公共子序列的方法如下，以两个序列 X、Y 为例子：

设有二维数组 f[i][j] 表示 X 的 i 位和 Y 的 j 位之前的最长公共子序列的长度，则有：

f[1][1] = same(1,1)

f[i][j] = max{f[i − 1][j − 1] +same(i,j), f[i − 1][j] ,f[i][j − 1]}

其中，same(a,b)当 X 的第 a 位与 Y 的第 b 位完全相同时为“1”，否则为“0”。

此时，f[i][j]中最大的数便是 X 和 Y 的最长公共子序列的长度，依据该数组回溯，便可找出最长公共子序列。

该算法的空间、时间复杂度均为O(n²)，经过优化后，空间复杂度可为O(n)，时间复杂度为O(nlogn)。

以下是此算法的java代码：

    下面咱们来了解一种不同于动态规划法的一种新的求解最长公共子序列问题的方法,该算法主要是把求解公共字符串问题转化为求解矩阵L(p,m)的问题，在利用定理求解矩阵的元素过程中（1）while(i<k),L(k,i)=null，
                  （2）while(L(k,i)=k),L(k,i+1)=L(k,i+2)=…L(k,m)=k；

    求出每列元素，一直到发现第p+1 行都为null 时退出循环，得出矩阵L(k,m)后，B[L(1,m-p+1)]B[L(2,m-p+2)]…B[L(p,m)]即为A 和B 的LCS，其中p 为LCS 的长度。

6.1 主要定义及定理

• 定义 1 子序列(Subsequence)：给定字符串A=A[1]A[2]…A[m]，(A[i]是A 的第i 个字母，A[i]∈字符集Σ，l<= i<m = A ， A 表示字符串A 的长度)，字符串B 是A 的子序列是指B=A[ 1 i ]A[ 2 i ]…A[ k i ],其中1 i < 2 i <…< k i 且k<=m.
• 定义2 公共子序列(Common Subsequence)：给定字符串A、B、C，C 称为A 和B 的公共子序列是指C 既是A 的子序列，又是B 的子序列。
• 定义3 最长公共子序列(Longest Common Subsequence 简称LCS)：给定字符串A、B、C，C 称为A 和B 的最长公共子序列是指C 是A 和B 的公共子序列，且对于A 和B 的任意公共子序列D，都有D <= C 。给定字符串A 和B，A =m，B =n，不妨设m<=n，LCS 问题就是要求出A 和B 的LCS。
• 定义4 给定字符串A=A[1]A[2]…A[m]和字符串B=B[1]B[2]…[n]，A( 1:i)表示A 的连续子序列A[1]A[2]…A[i]，同样B(1:j)表示B 的连续子序列B[1]B[2]…[j]。Li(k)表示所有与字符串A(1:i) 有长度为k 的LCS 的字符串B(l:j) 中j 的最小值。用公式表示就是Li(k)=Minj(LCS(A(1:i)，B(l:j))=k) [3]。

定理1 ∀ i∈[1，m]，有Li(l)<Li(2)<Li(3)<…<Li(m) .
定理2 ∀i∈[l，m-1]，∀k∈[l，m]，有i 1 L + (k)<= i L (k).
定理3 ∀ i∈[l，m-1]， ∀ k∈[l，m-l]，有i L (k)< i 1 L + (k+l).
以上三个定理都不考虑Li(k)无定义的情况。
定理4[3] i 1 L + (k)如果存在，那么它的取值必为: i 1 L + (k)=Min(j, i L (k))。这里j 是满足以下条件的最小整数:A[i+l]=B[j]且j> i L (k-1)。

    矩阵中元素L(k，i)=Li(k)，这里(1<i<=m，1<k<=m)，null 表示L(k,i)不存在。当i<k 时，显然L(k，i)不存在。
    设p=Maxk(L(k ， m) ≠ null) ， 可以证明L 矩阵中L(p,m) 所在的对角线,L(1,m-p+1),L(2,m-p+2)…L(p-1,m-1),L(p,m) 所对应的子序列B[L(1,m-p+1)]B[L(2,m-p+2)]…B[L(p,m)]即为A 和B 的LCS，p 为该LCS 的长度。这样，LCS 问题的求解就转化为对m m L × 矩阵的求解。

6.2 算法思想
    根据定理,第一步求出第一行元素,L(1,1),L(1,2),…L(1,m),第二步求第二行,一直到发现第p+1 行都为null 为止。在计算过程中遇到i<k 时,L(k,i)=null, 及L(k,i)=k时,L(k,i+1)=L(k,i+2)=…L(k,m)=k。这样,计算每行的时间复杂度为O(n),则整个时间复杂度为O(pn)。在求L 矩阵的过程中不用存储整个矩阵,只需存储当前行和上一行即可。空间复杂度为O(m+n)。

    下面给出一个例子来说明:给定字符串A 和B，A=acdabbc，B=cddbacaba，(m= A =7，n= B =9)。按照定理给出的递推公式，求出A 和B 的L 矩阵如图2，其中的$表示NULL。

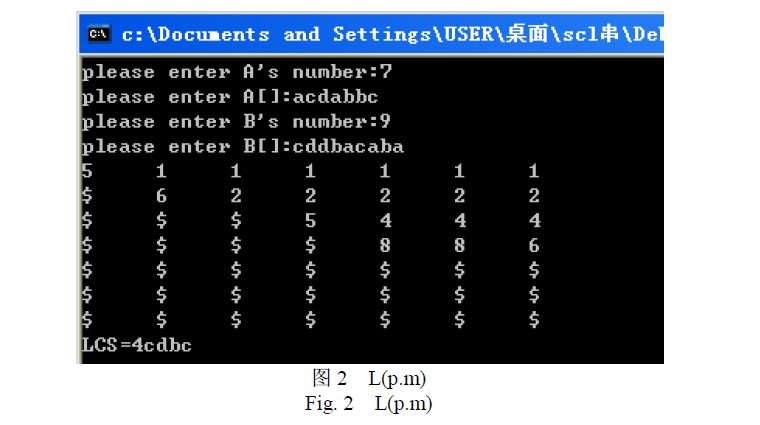
    则A 和B 的LCS 为B[1]B[2]B[4]B[6]=cdbc,LCS 的长度为4。

6.3 算法伪代码
算法 L(A,B,L)
输入 长度分别为m,n 的字符串A,B
输出 A,B 的最长公共子序列LCS

6.4 结语
    本节主要描述区别于动态规划法的一种新的求解最长公共子序列问题的方法，在不影响精确度的前提下，提高序列匹配的速度，根据定理i 1 L + (k)=Min(j, i L (k))得出矩阵，在求解矩阵的过程中对最耗时的L(p,m)进行条件约束优化。我们在Intel(R) Core(TM)2 Quad 双核处理器、1G 内存，软件环境：windows xp 下试验结果证明，本文算法与其他经典的比对算法相比,不但能够取得准确的结果,而且速度有了较大的提高（本节参考了刘佳梅女士的论文）。

    若有任何问题，恳请不吝指正。谢谢各位。完。