李宏毅深度学习
Gradient Descent of neural network:
- n e u r a l n e t w o r k neural\ \ network neural network的参数: θ = { w 1 , w 2 , ⋯ , b 1 , b 2 , ⋯ } θ=\{w_1,w_2,\cdots,b_1,b_2,\cdots \} θ={w1,w2,⋯,b1,b2,⋯}
- 计算参数 θ θ θ对于损失函数L的导数 Δ L ( θ ) \Delta L(θ) ΔL(θ)
Δ L ( θ ) = [ ∂ L ( θ ) / ∂ w 1 ∂ L ( θ ) / ∂ w 2 ⋯ ∂ L ( θ ) / ∂ b 1 ∂ L ( θ ) / ∂ b 2 ⋯ ] \Delta L(θ)=\begin{bmatrix} \partial L(θ)/\partial w_1 \\ \\ \partial L(θ)/\partial w_2 \\ \\\cdots \\ \\ \partial L(θ)/\partial b_1 \\ \\ \partial L(θ)/\partial b_2 \\ \cdots \end{bmatrix} ΔL(θ)=⎣ ⎡∂L(θ)/∂w1∂L(θ)/∂w2⋯∂L(θ)/∂b1∂L(θ)/∂b2⋯⎦ ⎤ - 更新参数: θ = θ − η Δ L ( θ ) θ = θ -\eta\Delta L(θ) θ=θ−ηΔL(θ)
Δ L ( θ ) \Delta L(θ) ΔL(θ)可以是一个上百万维的向量,计算十分的麻烦;所以 B a c k p r o p a g a t i o n Backpropagation Backpropagation要做的是去高效的计算反向传播的梯度 Δ L ( θ ) \Delta L(θ) ΔL(θ)。
定义预测结果 y n y^n yn(理想模型)与实际结果 y ^ n \hat{y}^n y^n(现实模型)之间的距离为 l n l^n ln,即第 n n n单个样本的损失函数值是 l n l^n ln。
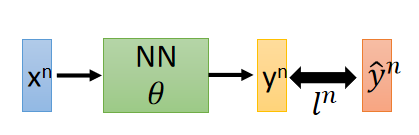
总体样本损失函数值表达式为:
L ( θ ) = ∑ n = 1 N l n ( θ ) L(θ)=\sum\limits_{n=1}^{N} {l^n(θ)} L(θ)=n=1∑Nln(θ)
对损失函数 L ( θ ) L(θ) L(θ)左右两边同时对 w w w求偏微分:
∂ L ( θ ) ∂ w = ∑ n = 1 N ∂ l n ( θ ) ∂ w \frac{\partial L(θ)}{\partial w}=\sum\limits_{n=1}^{N} \frac{\partial l^n(θ)}{\partial w} ∂w∂L(θ)=n=1∑N∂w∂ln(θ)
可以看出,我们仅需要对一个样本数据进行讨论,再将一个样本讨论的结论覆盖到整体样本上进行求和即可。所以下面的讨论都是基于一个样本的。
B a c k p r o p a g a t i o n Backpropagation Backpropagation可以分为 F o r w a r d p a s s Forward\ pass Forward pass和 B a c k w a r d p a s s Backward\ pass Backward pass两个部分,首先讨论 F o r w a r d p a s s Forward\ pass Forward pass。
Forward pass:
我们的目标是求出 ∂ l ∂ w \frac{\partial l}{\partial w} ∂w∂l;
将下图三角形部分的神经元拿出来单独讨论;
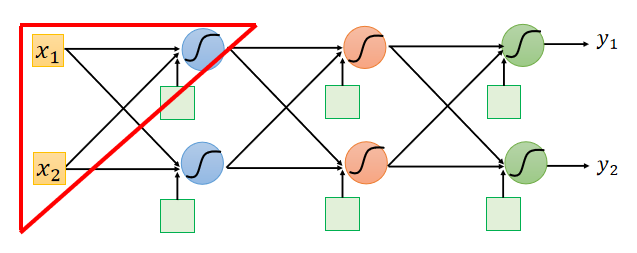
观察下面的图片,通过链式求导法则可以将 ∂ l ∂ w \frac{\partial l}{\partial w} ∂w∂l展开为:
∂ l ∂ w = ∂ z ∂ w ∂ l ∂ z \frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial l}{\partial z} ∂w∂l=∂w∂z∂z∂l
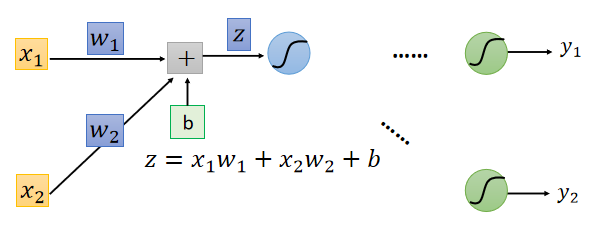
z z z的表达式在前向传播中给出来了, ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z的计算会很容易:
∂ z ∂ w 1 = x 1 \frac{\partial z}{\partial w_1}=x_1 ∂w1∂z=x1
∂ z ∂ w 2 = x 2 \frac{\partial z}{\partial w_2}=x_2 ∂w2∂z=x2
可以看出 z z z对 w w w的偏导等于与 w w w相联系的 i n p u t input input。
将这个结论扩展到网络的其他部分,如下图:
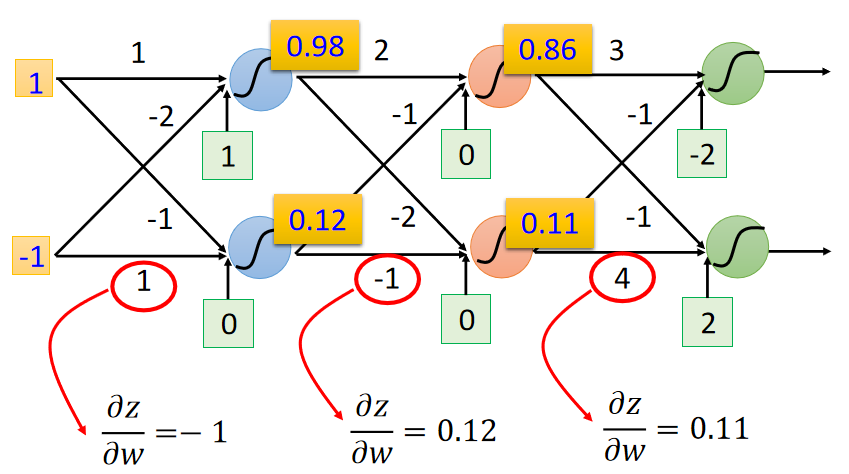
所以通过前向传播,计算每个神经节点的输入就能计算所有的 ∂ z ∕ ∂ w ∂z∕∂w ∂z∕∂w了。
Backward pass:
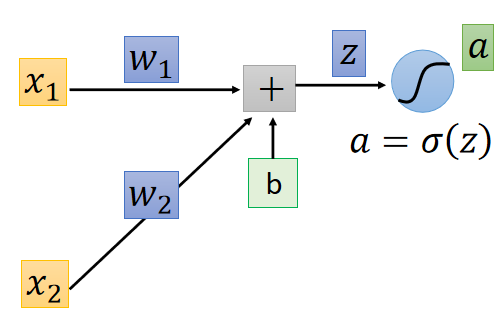
∂ l ∂ w = ∂ z ∂ w ∂ l ∂ z \frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial l}{\partial z} ∂w∂l=∂w∂z∂z∂l中的 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z通过 F o r w a r d p a s s Forward\ pass Forward pass就能够计算出来。接下来计算 ∂ l ∂ z \frac{\partial l}{\partial z} ∂z∂l部分,根据链式法则:
∂ l ∂ z = ∂ a ∂ z ∂ l ∂ a (1) \frac{∂l}{∂z}=\frac{∂a}{∂z}\frac{∂l}{∂a} \tag 1 ∂z∂l=∂z∂a∂a∂l(1)
∂ a ∂ z \frac{∂a}{∂z} ∂z∂a就是对激活函数求导,假设使用的激活函数是 s i g m o i d sigmoid sigmoid,那么 ∂ a ∂ z = σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \frac{∂a}{∂z}=σ'(z)=σ(z)(1-σ(z)) ∂z∂a=σ′(z)=σ(z)(1−σ(z))
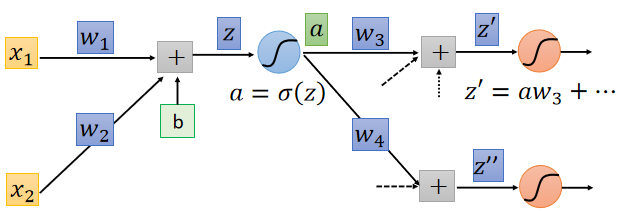
所以主要问题在于 ∂ l ∂ a \frac{∂l}{∂a} ∂a∂l的计算,观察上图, ∂ l ∂ a \frac{∂l}{∂a} ∂a∂l可以按照链式法则继续展开为:
∂ l ∂ a = ∂ z ′ ∂ a ∂ l ∂ z ′ + ∂ z ′ ′ ∂ a ∂ l ∂ z ′ ′ \frac{∂l}{∂a}=\frac{∂z'}{∂a}\frac{∂l}{∂z'}+\frac{∂z''}{∂a}\frac{∂l}{∂z''} ∂a∂l=∂a∂z′∂z′∂l+∂a∂z′′∂z′′∂l
根据 z ′ z' z′和 z ′ ′ z'' z′′的表达式可以计算 ∂ z ′ ∂ a = w 1 \frac{∂z'}{∂a}=w_1 ∂a∂z′=w1、 ∂ z ′ ′ ∂ a = w 2 \frac{∂z''}{∂a}=w_2 ∂a∂z′′=w2。
带入到(1)中:
∂ l ∂ z = σ ′ ( z ) [ w 3 ∂ l ∂ z ′ + w 4 ∂ l ∂ z ′ ′ ] (2) \frac{∂l}{∂z}=σ'(z)[w_3\frac{∂l}{∂z'}+w_4\frac{∂l}{∂z''}] \tag2 ∂z∂l=σ′(z)[w3∂z′∂l+w4∂z′′∂l](2)
如下图,表达式 ( 2 ) (2) (2)的含义就像从后面向前面传播:
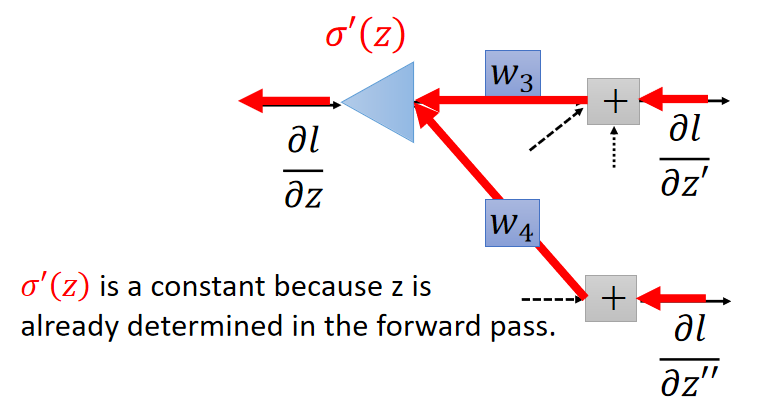
接下来求出 ∂ l ∂ z ′ \frac{∂l}{∂z'} ∂z′∂l和 ∂ l ∂ z ′ ′ \frac{∂l}{∂z''} ∂z′′∂l,就可以计算出 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l。
分两种情况讨论:
-
− C a s e 1 − -Case\ 1- −Case 1−:
z ′ z' z′和 z ′ ′ z'' z′′是连接的是输出层,如下图:
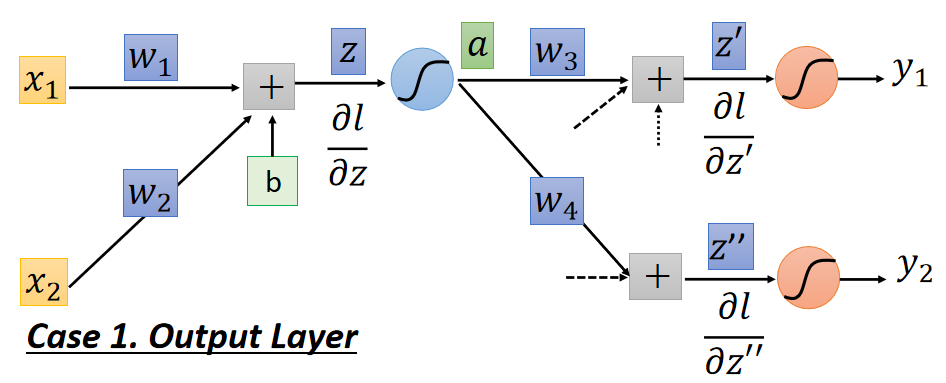
链式法则展开:
∂ l ∂ z ′ = ∂ y 1 ∂ z ′ ∂ l ∂ y 1 \frac{∂l}{∂z'}=\frac{∂y_1}{∂z'}\frac{∂l}{∂y_1} ∂z′∂l=∂z′∂y1∂y1∂l ∂ l ∂ z ′ ′ = ∂ y 2 ∂ z ′ ′ ∂ l ∂ y 2 \frac{∂l}{∂z''}=\frac{∂y_2}{∂z''}\frac{∂l}{∂y_2} ∂z′′∂l=∂z′′∂y2∂y2∂l
l l l对 y y y求导可以通过损失函数表达式计算, y y y对 z z z求偏导其实就是激活函数的求导,这时候工作 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l就计算完成了。 -
− C a s e 2 − -Case\ 2- −Case 2−:
z ′ z' z′和 z ′ ′ z'' z′′是连接的不是输出层,如下图:
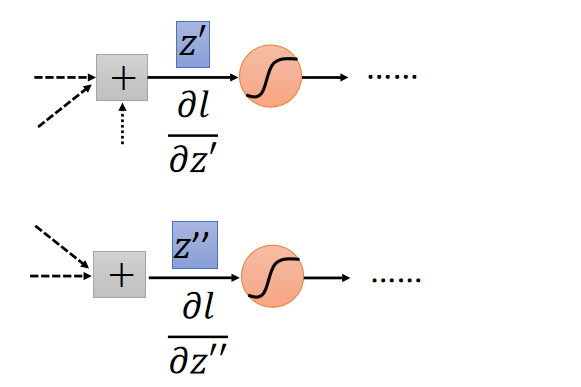
其实这就是个套娃的过程,计算当前层的 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l需要计算下一层的 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l,计算下一层的 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l需要计算下下层的 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l。如下图:
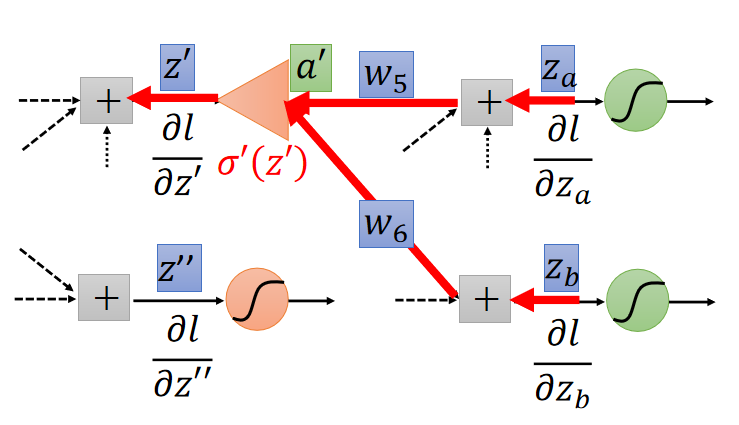
所以要做的是递归计算 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l,直到最后一层。
为了方便计算,从输出层开始计算 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l,再通过反向传播向前传递,如下图:
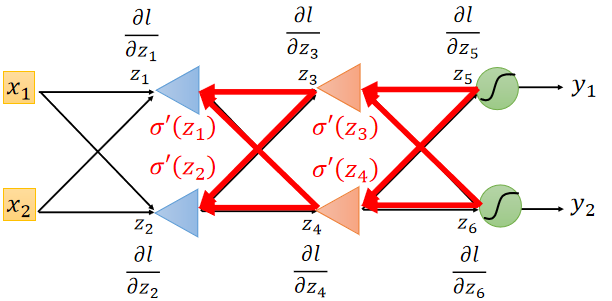
以上就是 B a c k w a r d p a s s Backward pass Backwardpass的过程。
总结:
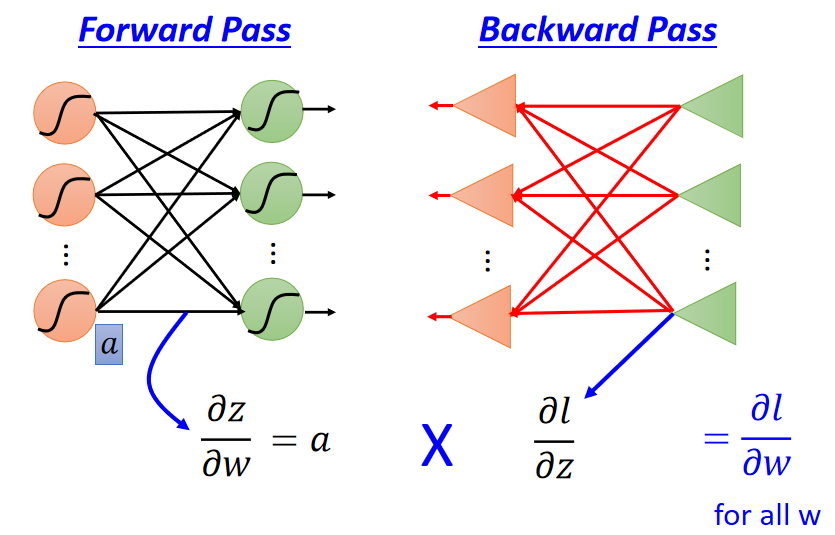
计算梯度 ∂ l ∂ w = ∂ z ∂ w ∂ l ∂ z \frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial l}{\partial z} ∂w∂l=∂w∂z∂z∂l:
- F o r w a r d P a s s Forward\ Pass Forward Pass(正向传递)计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z;
- B a c k w a r d P a s s Backward\ Pass Backward Pass(反向传递)计算 ∂ l ∂ z \frac{∂l}{∂z} ∂z∂l








![MySQL MINUS-差集 [猿教程]](https://img-blog.csdnimg.cn/img_convert/da4d2d5874d051cd48b4f1cc94747295.png)