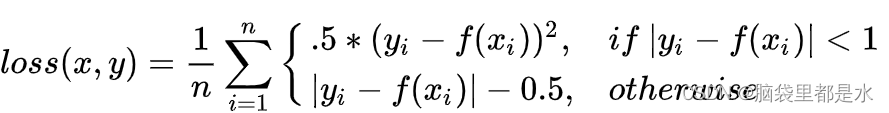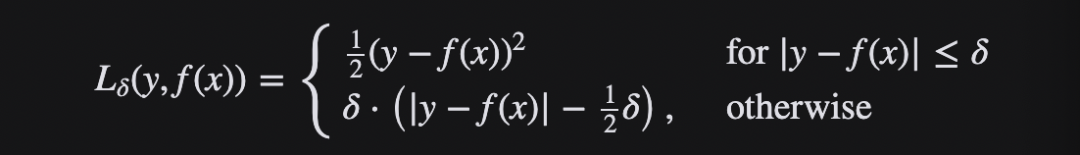1. 概述

在机器学习算法中，有一个重要的概念就是损失函数（Loss Function）。损失函数的作用就是度量模型的预测值$f\left(\mathbf{x}\right)$与真实值$\mathbf{y}$之间的差异程度的函数，且是一个非负实值函数。

对于分类问题损失函数通常可以表示成损失项和正则项的和，即有如下的形式：

$$J\left(\mathbf{w}\right)=\sum _{i}L\left(m_i\left(\mathbf{w}\right)\right)+\lambda R\left(\mathbf{w}\right)$$

其中，$L\left(m_i\left(\mathbf{w}\right)\right)$为损失项，$R\left(\mathbf{w}\right)$为正则项。$m_i$的具体形式如下：

$$m_i=y^{\left(i\right)}{f}_{\mathbf{w}}\left({\mathbf{x}}^{\left(i\right)}\right)$$

y ( i ) ∈ { − 1 , 1 } y^{\left ( i \right )}\in \left \{ -1,\;1 \right \} y(i)∈{−1,1}

$$f_{\mathbf{w}}\left({\mathbf{x}}^{\left(i\right)}\right)={\mathbf{w}}^T{\mathbf{x}}^{(i)}$$

对于损失项，主要的形式有：

• 0-1损失
• Log损失
• Hinge损失
• 指数损失
• 感知损失

2. 0-1损失函数

在分类问题中，可以使用函数的正负号来进行模式判断，函数值本身的大小并不是很重要，0-1损失函数比较的是预测值$f_{\mathbf{w}}\left({\mathbf{x}}^{\left(i\right)}\right)$与真实值$y^{\left(i\right)}$的符号是否相同，0-1损失的具体形式如下：

$$L_{01}\left(m\right)=\{\begin{array}{ll}0& \text{ if }m⩾0\\ 1& \text{ if }m<0\end{array}$$

以上的函数等价于下述的函数：

$$\frac{1}{2}\left(1-sign\left(m\right)\right)$$

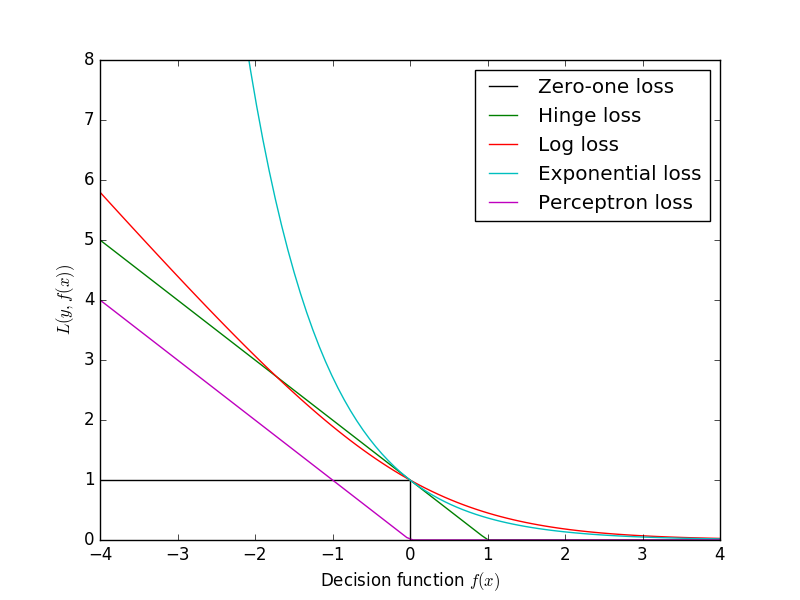
0-1损失并不依赖$m$值的大小，只取决于$m$的正负号。0-1损失是一个非凸的函数，在求解的过程中，存在很多的不足，通常在实际的使用中将0-1损失函数作为一个标准，选择0-1损失函数的代理函数作为损失函数。

3. Log损失函数

3.1. Log损失

Log损失是0-1损失函数的一种代理函数，Log损失的具体形式如下：

$$log\left(1+exp\left(-m\right)\right)$$

运用Log损失的典型分类器是Logistic回归算法。

3.2. Logistic回归算法的损失函数

对于Logistic回归算法，分类器可以表示为：

$$p\left(y\mid \mathbf{x};\mathbf{w}\right)=\sigma {\left({\mathbf{w}}^T\mathbf{x}\right)}^y{\left(1-\sigma \left({\mathbf{w}}^T\mathbf{x}\right)\right)}^{\left(1-y\right)}$$

其中， y ∈ { 0 , 1 } y\in \left \{ 0,1 \right \} y∈{0,1}。为了求解其中的参数$ \mathbf{w}$，通常使用极大似然估计的方法，具体的过程如下：

1、似然函数

$$L\left(\mathbf{w}\right)=\prod _{i=1}^n\sigma {\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}\right)}^{y^{\left(i\right)}}{\left(1-\sigma \left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}\right)\right)}^{\left(1-y^{\left(i\right)}\right)}$$

其中，

$$\sigma \left(x\right)=\frac{1}{1+exp\left(-x\right)}$$

2、log似然

$$logL\left(\mathbf{w}\right)=\sum _{i=1}^n{y}^{\left(i\right)}log\left(\sigma \left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}\right)\right)+\left(1-y^{\left(i\right)}\right)log\left(1-\sigma \left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}\right)\right)$$

3、需要求解的是使得log似然取得最大值的$ \mathbf{w}$，可以转换为求最小值：

$$-logL\left(\mathbf{w}\right)=-\sum _{i=1}^n{y}^{\left(i\right)}log\left(\sigma \left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}\right)\right)+\left(1-y^{\left(i\right)}\right)log\left(1-\sigma \left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}\right)\right)$$

这便是交叉熵的具体形式。

3.3. 两者的等价

由于Log损失的具体形式为：

$$log\left(1+exp\left(-m\right)\right)$$

其中，$m=y^{\left(i\right)}{\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}$， y ( i ) ∈ { − 1 , 1 } y^{\left ( i \right )}\in \left \{ -1,1 \right \} y(i)∈{−1,1}，Log损失函数的具体形式为：

$$\underset{\mathbf{w}}{\min }\sum _{i=1}^{n}log\left\{1+exp\left(-y^{\left(i\right)}{\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}\right)\right\}$$

Logistic回归与Log损失具有相同的形式，故两者是等价的。Log损失与0-1损失的关系可见下图。

4. Hinge损失函数

4.1. Hinge损失

Hinge损失是0-1损失函数的一种代理函数，Hinge损失的具体形式如下：

$$max\left(0,1-m\right)$$

运用Hinge损失的典型分类器是SVM算法。

4.2. SVM的损失函数

对于软间隔支持向量机，允许在间隔的计算中出现少许的误差$\vec{\xi }=\left({\xi }_1,\cdots ,{\xi }_n\right)$，其优化的目标为：

$$\underset{\mathbf{w},\gamma ,\xi }{\min }\left[\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\sum _{i=1}^n{\xi }_i\right]$$

约束条件为：

$$\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\gamma \right)y^{\left(i\right)}⩾1-{\xi }_i,{\xi }_i\ge 0$$

4.3. 两者的等价

对于Hinge损失：

$$max\left(0,1-m\right)$$

优化的目标是要求：

$$\underset{\mathbf{w}}{\min }\left[\sum _{i=1}^{n}max\left(0,1-f_{\mathbf{w}}\left({\mathbf{x}}^{\left(i\right)}\right)y^{\left(i\right)}\right)\right]$$

在上述的函数$f_{\mathbf{w}}\left({\mathbf{x}}^{\left(i\right)}\right)$中引入截距$\gamma $，即：

$$f_{\mathbf{w},\gamma }\left({\mathbf{x}}^{\left(i\right)}\right)={\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\gamma$$

并在上述的最优化问题中增加$L_2$正则，即变成：

$$\underset{\mathbf{w},\gamma }{\min }\left[C\sum _{i=1}^{n}max\left(0,1-f_{\mathbf{w},\gamma }\left({\mathbf{x}}^{\left(i\right)}\right)y^{\left(i\right)}\right)+\frac{1}{2}{\Vert \mathbf{w}\Vert }^2\right]$$

至此，令下面的不等式成立：

$$max\left(0,1-f_{\mathbf{w},\gamma }\left(\mathbf{x}\right)y\right)=\underset{\xi }{\min }\xi$$

约束条件为：

$$\xi ⩾1-f_{\mathbf{w},\gamma }\left(\mathbf{x}\right)y;\xi ⩾0$$

则Hinge最小化问题变成：

$$\underset{\mathbf{w},\gamma ,\xi }{\min }\left[C\sum _{i=1}^n{\xi }_i+\frac{1}{2}{\Vert \mathbf{w}\Vert }^2\right]$$

约束条件为：

$${\xi }_i⩾1-\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\gamma \right)y^{\left(i\right)};{\xi }_i⩾0$$

这与软间隔的SVM是一致的，说明软间隔SVM是在Hinge损失的基础上增加了$L_2$正则。

5. 指数损失

5.1. 指数损失

指数损失是0-1损失函数的一种代理函数，指数损失的具体形式如下：

$$exp\left(-m\right)$$

运用指数损失的典型分类器是AdaBoost算法。

5.2. AdaBoost基本原理

AdaBoost算法是对每一个弱分类器以及每一个样本都分配了权重，对于弱分类器${\phi }_j$的权重为：

$${\theta }_j=\frac{1}{2}log\frac{1-R\left({\phi }_j\right)}{R\left({\phi }_j\right)}$$

其中，$R\left({\phi }_j\right)$表示的是误分类率。对于每一个样本的权重为：

$$w_i=\frac{exp\left(-f\left(x^{\left(i\right)}{y}^{\left(i\right)}\right)\right)}{{\sum }_n\left[exp\left(-f\left(x^{\left(i\right)}{y}^{\left(i\right)}\right)\right)\right]}$$

最终通过对所有分类器加权得到最终的输出。

5.3. 两者的等价

对于指数损失函数：

$$exp\left(-m\right)$$

可以得到需要优化的损失函数：

$$\underset{\theta }{\min }\left[\sum _{i=1}^{n}exp\left(-f_{\theta }\left({\mathbf{x}}^{\left(i\right)}\right)y^{\left(i\right)}\right)\right]$$

假设$\tilde{f}$表示已经学习好的函数，则有：

$$\underset{\theta ,\phi }{\min }\left[\sum _{i=1}^{n}exp\left(-\left\{{\tilde{f}}_{\theta }\left({\mathbf{x}}^{\left(i\right)}\right)+\theta \phi \left({\mathbf{x}}^{\left(i\right)}\right)\right\}{y}^{\left(i\right)}\right)\right]$$

$$=\underset{\theta ,\phi }{\min }\left[\sum _{i=1}^n\widetilde{w_i}exp\left(-\theta \phi \left({\mathbf{x}}^{\left(i\right)}\right)y^{\left(i\right)}\right)\right]$$

而：

∑ i = 1 n w i ~ e x p ( − θ φ ( x ( i ) ) y ( i ) ) = { e x p ( θ ) − e x p ( − θ ) } ∑ i = 1 n w i ~ 2 ( 1 − φ ( x ( i ) ) y ( i ) ) + e x p ( − θ ) ∑ i = 1 n w i ~ \sum_{i=1}^{n}\tilde{w_i}exp\left ( -\theta \varphi \left ( \mathbf{x}^{\left ( i \right )} \right ) y^{\left ( i \right )} \right )\\ =\left \{ exp\left ( \theta \right ) - exp\left ( -\theta \right ) \right \}\sum_{i=1}^{n}\frac{\tilde{w_i}}{2}\left ( 1-\varphi \left ( \mathbf{x}^{\left ( i \right )} \right ) y^{\left ( i \right )} \right )+exp\left ( -\theta \right )\sum_{i=1}^{n}\tilde{w_i} i=1∑n​wi​~​exp(−θφ(x(i))y(i))={exp(θ)−exp(−θ)}i=1∑n​2wi​~​​(1−φ(x(i))y(i))+exp(−θ)i=1∑n​wi​~​

通过最小化$\varphi $，可以得到：

$$\hat{\phi }=\underset{\phi }{\mathrm{argmin}}\sum _{i=1}^n\frac{{\tilde{w}}_i}{2}\left(1-\phi \left({\mathbf{x}}^{\left(i\right)}\right)y^{\left(i\right)}\right)$$

将其代入上式，进而对$\theta $求最优解，得：

$$\hat{\theta }=\frac{1}{2}log\frac{1-\hat{R}}{\hat{R}}$$

其中，

$$\hat{R}=\left\{\sum _{i=1}^n\frac{{\tilde{w}}_i}{2}\left(1-\phi \left({\mathbf{x}}^{\left(i\right)}\right)y^{\left(i\right)}\right)\right\}/\left\{\sum _{i=1}^n{\tilde{w}}_i\right\}$$

可以发现，其与AdaBoost是等价的。

6. 感知损失

6.1. 感知损失

感知损失是Hinge损失的一个变种，感知损失的具体形式如下：

$$max\left(0,-m\right)$$

运用感知损失的典型分类器是感知机算法。

6.2. 感知机算法的损失函数

感知机算法只需要对每个样本判断其是否分类正确，只记录分类错误的样本，其损失函数为：

$$\underset{\mathbf{w},\mathbf{b}}{\min }\left[-\sum _{i=1}^n{y}^{\left(i\right)}\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\mathbf{b}\right)\right]$$

5.3. 两者的等价

对于感知损失：

$$max\left(0,-m\right)$$

优化的目标为：

$$\underset{\mathbf{w}}{\min }\left[\sum _{i=1}^{n}max\left(0,-f_{\mathbf{w}}\left({\mathbf{x}}^{\left(i\right)}\right)y^{\left(i\right)}\right)\right]$$

在上述的函数$f_{\mathbf{w}}\left({\mathbf{x}}^{\left(i\right)}\right)$中引入截距$\mathbf{b}$，即：

$$f_{\mathbf{w},\gamma }\left({\mathbf{x}}^{\left(i\right)}\right)={\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\mathbf{b}$$

上述的形式转变为：

$$\underset{\mathbf{w},\mathbf{b}}{\min }\left[\sum _{i=1}^{n}max\left(0,-\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\mathbf{b}\right)y^{\left(i\right)}\right)\right]$$

对于max函数中的内容，可知：

$$max\left(0,-\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\mathbf{b}\right)y^{\left(i\right)}\right)⩾0$$

对于错误的样本，有：

$$max\left(0,-\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\mathbf{b}\right)y^{\left(i\right)}\right)=-\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\mathbf{b}\right)y^{\left(i\right)}$$

类似于Hinge损失，令下式成立：

$$max\left(0,-f_{\mathbf{w},\mathbf{b}}\left(\mathbf{x}\right)y\right)=\underset{\xi }{\min }\xi$$

约束条件为：

$$\xi ⩾-f_{\mathbf{w},\mathbf{b}}\left(\mathbf{x}\right)y$$

则感知损失变成：

$$\underset{\xi }{\min }\left[\sum _{i=1}^n{\xi }_i\right]$$

即为：

$$\underset{\mathbf{w},\mathbf{b}}{\min }\left[-\sum _{i=1}^n{y}^{\left(i\right)}\left({\mathbf{w}}^T{\mathbf{x}}^{\left(i\right)}+\mathbf{b}\right)\right]$$

Hinge损失对于判定边界附近的点的惩罚力度较高，而感知损失只要样本的类别判定正确即可，而不需要其离判定边界的距离，这样的变化使得其比Hinge损失简单，但是泛化能力没有Hinge损失强。

import matplotlib.pyplot as plt
import numpy as npxmin, xmax = -4, 4
xx = np.linspace(xmin, xmax, 100)
plt.plot([xmin, 0, 0, xmax], [1, 1, 0, 0], 'k-', label="Zero-one loss")
plt.plot(xx, np.where(xx < 1, 1 - xx, 0), 'g-', label="Hinge loss")
plt.plot(xx, np.log2(1 + np.exp(-xx)), 'r-', label="Log loss")
plt.plot(xx, np.exp(-xx), 'c-', label="Exponential loss")
plt.plot(xx, -np.minimum(xx, 0), 'm-', label="Perceptron loss")plt.ylim((0, 8))
plt.legend(loc="upper right")
plt.xlabel(r"Decision function $f(x)$")
plt.ylabel("$L(y, f(x))$")
plt.show()

参考文章

[1] Advice for applying Machine Learning

[2] 损失函数（Loss Function）

[3] Schroff F , Kalenichenko D , Philbin J . FaceNet: A Unified Embedding for Face Recognition and Clustering[J]. IEEE, 2015.