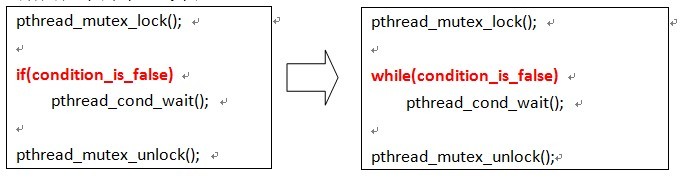
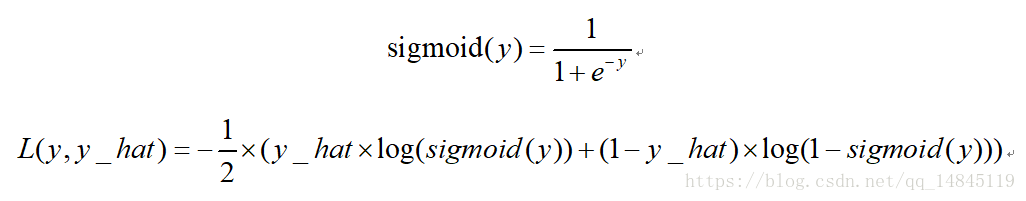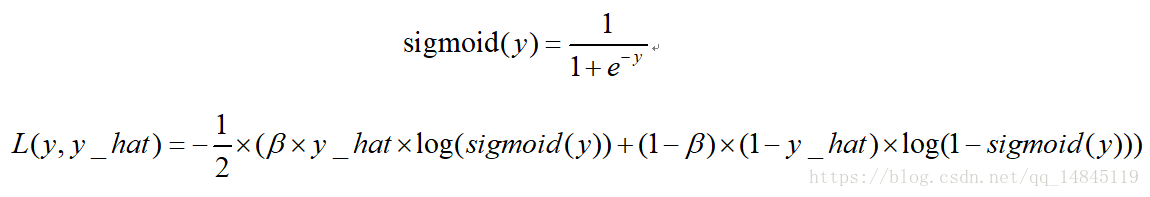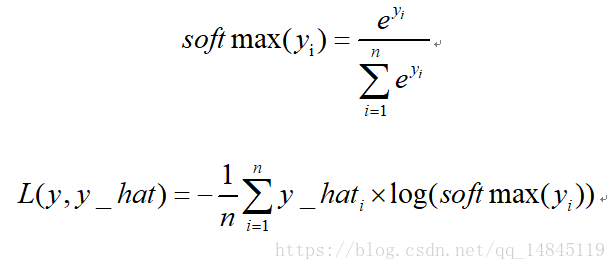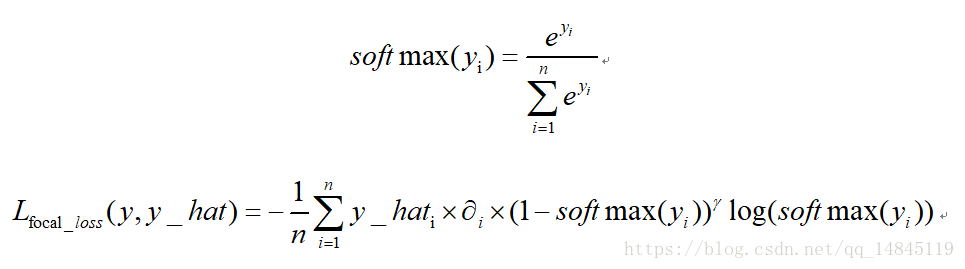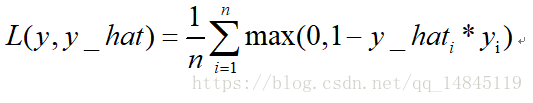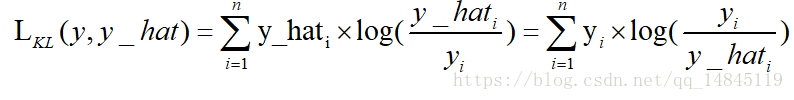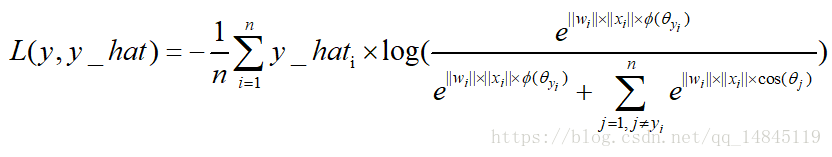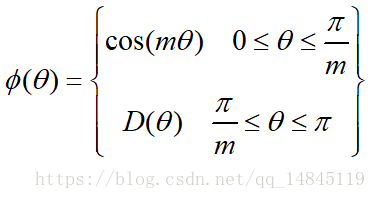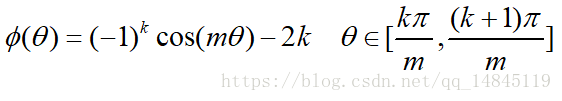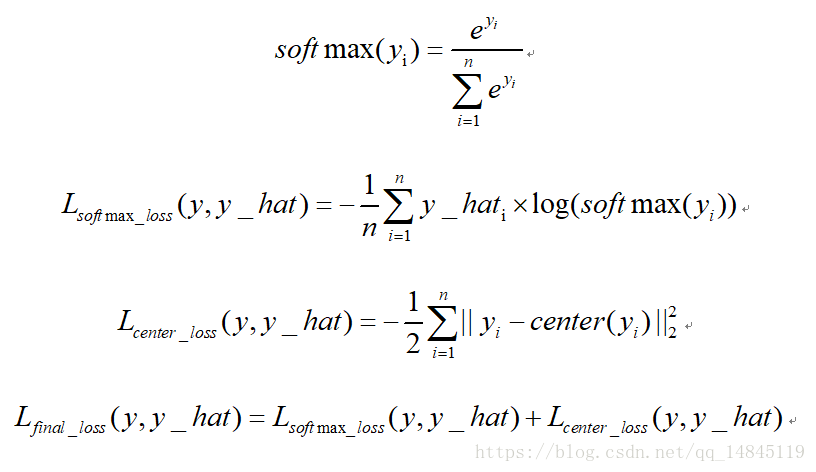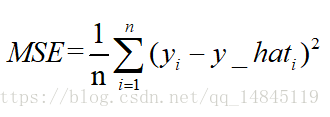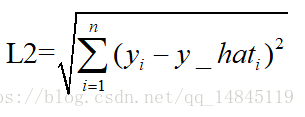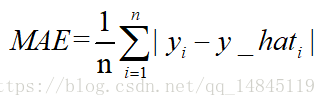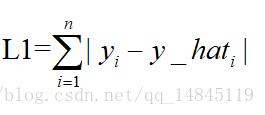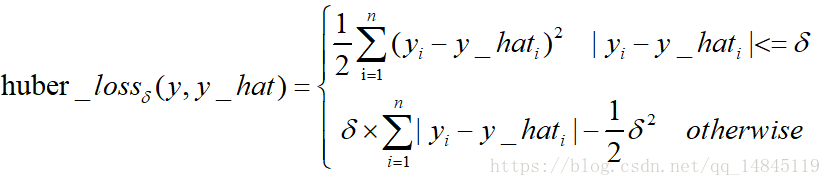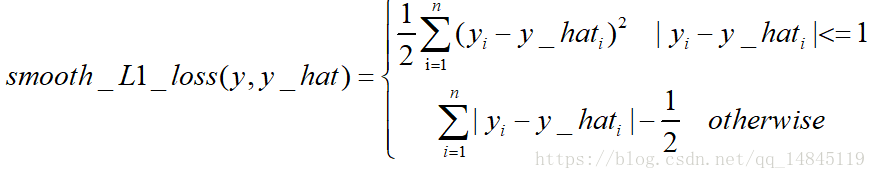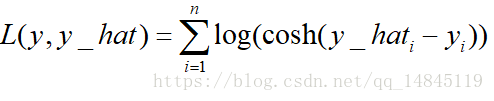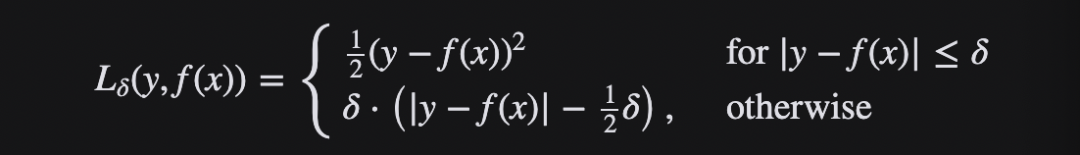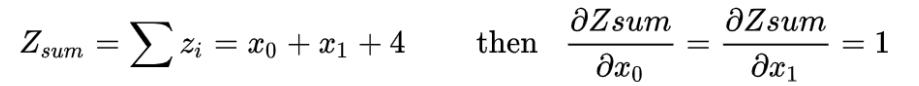损失函数loss大总结

分类任务loss:

二分类交叉熵损失sigmoid_cross_entropy：

TensorFlow 接口：

tf.losses.sigmoid_cross_entropy(multi_class_labels,logits,weights=1.0,label_smoothing=0,scope=None,loss_collection=tf.GraphKeys.LOSSES,reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)
tf.nn.sigmoid_cross_entropy_with_logits(_sentinel=None,labels=None,logits=None,name=None
)

keras 接口：

binary_crossentropy(y_true, y_pred)

二分类平衡交叉熵损失balanced_sigmoid_cross_entropy：

该损失也是用于2分类的任务，相比于sigmoid_cross_entrop的优势在于引入了平衡参数，可以进行正负样本的平衡，得到比sigmoid_cross_entrop更好的效果。

多分类交叉熵损失softmax_cross_entropy：

TensorFlow 接口：

tf.losses.softmax_cross_entropy(onehot_labels,logits,weights=1.0,label_smoothing=0,scope=None,loss_collection=tf.GraphKeys.LOSSES,reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)
tf.nn.softmax_cross_entropy_with_logits(_sentinel=None,labels=None,logits=None,dim=-1,name=None
)
tf.nn.sparse_softmax_cross_entropy_with_logits(_sentinel=None,labels=None,logits=None,name=None
)

keras 接口：

categorical_crossentropy(y_true, y_pred)
sparse_categorical_crossentropy(y_true, y_pred)

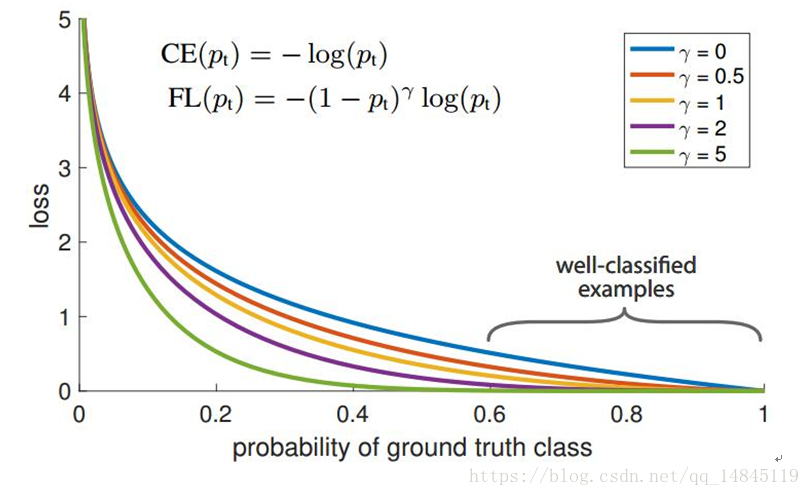
focal loss：

focal loss为凯明大神的大作，主要用于解决多分类任务中样本不平衡的现象，可以获得比softmax_cross_entropy更好的分类效果。

论文中α=0.25，γ=2效果最好。

dice loss(iou loss):

2分类任务时使用的loss，本质就是不断学习，使得交比并越来越大。

TensorFlow 接口：

def dice_coefficient(y_true_cls, y_pred_cls):'''dice loss:param y_true_cls::param y_pred_cls::return:'''eps = 1e-5intersection = tf.reduce_sum(y_true_cls * y_pred_cls )union = tf.reduce_sum(y_true_cls ) + tf.reduce_sum(y_pred_cls) + epsloss = 1. - (2 * intersection / union)tf.summary.scalar('classification_dice_loss', loss)return loss

GIOU loss(Generalized-IOU loss)：

出自论文，Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression，cvpr2019

yolov5中也有使用，

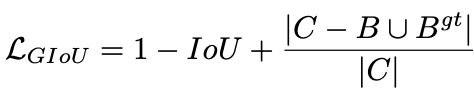
先计算两个框的最小闭包区域面积 [公式] (通俗理解：同时包含了预测框和真实框的最小框的面积)，再计算出IoU，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用IoU减去这个比重得到GIoU。

两个框的最小闭包区域面积Ac = 红色矩形面积

IoU = 黄色框和蓝色框的交集 / 并集

闭包区域中不属于两个框的区域占闭包区域的比重 = 蓝色面积 / 红色矩阵面积

GIoU = IoU - 比重

def Giou(rec1,rec2):#分别是第一个矩形左右上下的坐标x1,x2,y1,y2 = rec1 x3,x4,y3,y4 = rec2iou = Iou(rec1,rec2)area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))area_1 = (x2-x1)*(y1-y2)area_2 = (x4-x3)*(y3-y4)sum_area = area_1 + area_2w1 = x2 - x1   #第一个矩形的宽w2 = x4 - x3   #第二个矩形的宽h1 = y1 - y2h2 = y3 - y4W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)    #交叉部分的宽H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)    #交叉部分的高Area = W*H    #交叉的面积add_area = sum_area - Area    #两矩形并集的面积end_area = (area_C - add_area)/area_C    #闭包区域中不属于两个框的区域占闭包区域的比重giou = iou - end_area
return giou

DIOU loss（Distance-IoU Loss）:

出自论文，Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

，AAAI 2020

DIoU要比GIou更加符合目标框回归的机制，将目标与anchor之间的距离，重叠率以及尺度都考虑进去，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。

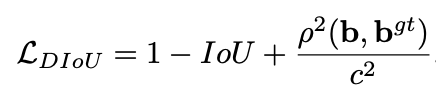
其中，b , bgt分别代表了预测框和真实框的中心点，且 ρ代表的是计算两个中心点间的欧式距离。c代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。

DIoU Loss的优点如下：

（1）和GIoU Loss类似，DIoU Loss在和目标框不重叠时，仍然可以为边界框提供移动方向。

（2）DIoU Loss可以直接最小化两个目标框的距离，因此比GIoU Loss收敛快得多。

（3）对于包含两个框在水平方向和垂直方向上这种情况，DIoU Loss可以使回归Loss 下降非常快，而GIoU Loss几乎退化为IoU Loss。

（4）DIoU还可以替换普通的IoU评价策略，应用于NMS中，使得NMS得到的结果更加合理和有效。

def Diou(bboxes1, bboxes2):rows = bboxes1.shape[0]cols = bboxes2.shape[0]dious = torch.zeros((rows, cols))if rows * cols == 0:#return diousexchange = Falseif bboxes1.shape[0] > bboxes2.shape[0]:bboxes1, bboxes2 = bboxes2, bboxes1dious = torch.zeros((cols, rows))exchange = True# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]w1 = bboxes1[:, 2] - bboxes1[:, 0]h1 = bboxes1[:, 3] - bboxes1[:, 1] w2 = bboxes2[:, 2] - bboxes2[:, 0]h2 = bboxes2[:, 3] - bboxes2[:, 1]area1 = w1 * h1area2 = w2 * h2center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2 center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2 center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:]) inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2]) out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:]) out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)inter_area = inter[:, 0] * inter[:, 1]inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2outer = torch.clamp((out_max_xy - out_min_xy), min=0)outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)union = area1+area2-inter_areadious = inter_area / union - (inter_diag) / outer_diagdious = torch.clamp(dious,min=-1.0,max = 1.0)if exchange:dious = dious.Treturn dious

CIOU loss（Complete-IoU Loss）：

同样出自论文，Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression，AAAI 2020

一个好的目标框回归损失应该考虑三个重要的几何因素：重叠面积，中心点距离，长宽比。GIoU为了归一化坐标尺度，利用IOU并初步解决了IoU为0无法优化的问题。然后DIoU损失在GIoU Loss的基础上考虑了边界框的重叠面积和中心点距离。所以还有最后一个点上面的Loss没有考虑到，即Anchor的长宽比和目标框之间的长宽比的一致性。基于这一点，论文提出了CIoU Loss。

应用于Yolov4

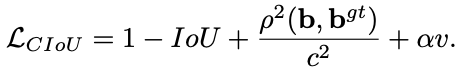
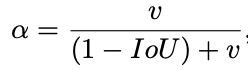
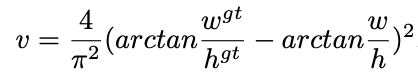
其中a是用来平衡比例的系数，v是用来衡量Anchor框和目标框之间的比例一致性。

def bbox_overlaps_ciou(bboxes1, bboxes2):rows = bboxes1.shape[0]cols = bboxes2.shape[0]cious = torch.zeros((rows, cols))if rows * cols == 0:return ciousexchange = Falseif bboxes1.shape[0] > bboxes2.shape[0]:bboxes1, bboxes2 = bboxes2, bboxes1cious = torch.zeros((cols, rows))exchange = Truew1 = bboxes1[:, 2] - bboxes1[:, 0]h1 = bboxes1[:, 3] - bboxes1[:, 1]w2 = bboxes2[:, 2] - bboxes2[:, 0]h2 = bboxes2[:, 3] - bboxes2[:, 1]area1 = w1 * h1area2 = w2 * h2center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)inter_area = inter[:, 0] * inter[:, 1]inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2outer = torch.clamp((out_max_xy - out_min_xy), min=0)outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)union = area1+area2-inter_areau = (inter_diag) / outer_diagiou = inter_area / unionwith torch.no_grad():arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)S = 1 - ioualpha = v / (S + v)w_temp = 2 * w1ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)cious = iou - (u + alpha * ar)cious = torch.clamp(cious,min=-1.0,max = 1.0)if exchange:cious = cious.Treturn cious

合页损失hinge_loss：

也叫铰链损失，是svm中使用的损失函数。

由于合页损失优化到满足小于一定gap距离就会停止优化，而交叉熵损失却是一直在优化，所以，通常情况下，交叉熵损失效果优于合页损失。

TensorFlow 接口：

tf.losses.hinge_loss(labels,logits,weights=1.0,scope=None,loss_collection=tf.GraphKeys.LOSSES,reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)

keras 接口：

hinge(y_true, y_pred)

Connectionisttemporal classification(ctc loss):

对于预测的序列和label序列长度不一致的情况下，可以使用ctc计算该2个序列的loss，主要用于文本分类识别和语音识别中。

TensorFlow 接口：

tf.nn.ctc_loss(labels,inputs,sequence_length,preprocess_collapse_repeated=False,ctc_merge_repeated=True,ignore_longer_outputs_than_inputs=False,time_major=True
)

keras 接口：

tf.keras.backend.ctc_batch_cost(y_true,y_pred,input_length,label_length
)

编辑距离 edit loss:

编辑距离，也叫莱文斯坦Levenshtein 距离，指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。
该损失函数的优势在于类似于ctc loss可以计算2个长度不等的序列的损失。
TensorFlow 接口：

tf.edit_distance(hypothesis,truth,normalize=True,name='edit_distance'
)

KL散度：

KL散度( Kullback–Leibler divergence)，也叫相对熵，是描述两个概率分布P和Q差异的一种方法。它是非对称的，这意味着D(P||Q) ≠ D(Q||P)。特别的，在信息论中，D(P||Q)表示当用概率分布Q来拟合真实分布P时，产生的信息损耗，其中P表示真实分布，Q表示P的拟合分布。

从上面式子可以看出，kl散度，也就是相对熵，其实就是交叉熵+一个常数项。

TensorFlow 接口：

tf.distributions.kl_divergence(distribution_a,distribution_b,allow_nan_stats=True,name=None
)tf.contrib.distributions.kl(
dist_a,dist_b,allow_nan =False,name=None
)

最大间隔损失large margin softmax loss:

用于拉大类间距离的损失函数，可以训练得到比传统softmax loss更好的分类效果。

最大间隔损失主要引入了夹角cos值进行距离的度量。假设bias为0的情况下，就可以得出如上的公式。

其中fai(seita)需要满足下面的条件。

为了进行距离的度量，在cos夹角中引入了参数m。该m为一个正整数，可以起到控制类间间隔的作用。M越大，类间间隔越大。当m=1时，等价于传统交叉熵损失。基本原理如下面公式

论文中提供的满足该条件的公式如下

中心损失center loss:

中心损失主要主要用于减少类内距离，虽然只是减少了累内距离，效果上却可以表现出累内距离小了，类间距离就可以增大的效果。该损失不可以直接使用，需要配合传统的softmax loss一起使用。可以起到比单纯softmax loss更好的分类效果。

回归任务loss:

均方误差mean squareerror（MSE）和L2范数:

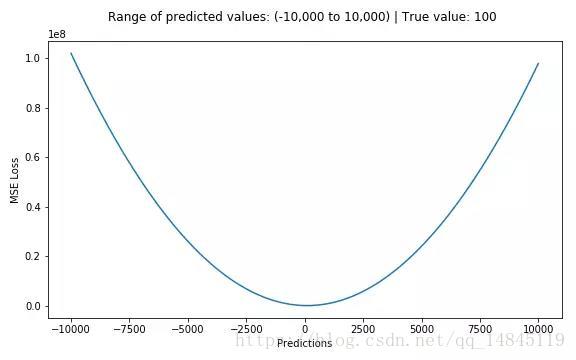
MSE表示了预测值与目标值之间差值的平方和然后求平均

L2损失表示了预测值与目标值之间差值的平方和然后开更方，L2表示的是欧几里得距离。

MSE和L2的曲线走势都一样。区别在于一个是求的平均np.mean()，一个是求的更方np.sqrt()

TensorFlow 接口：

tf.losses.mean_squared_error(labels,predictions,weights=1.0,scope=None,loss_collection=tf.GraphKeys.LOSSES,reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)
tf.metrics.mean_squared_error(labels,predictions,weights=None,metrics_collections=None,updates_collections=None,name=None
)

keras 接口：

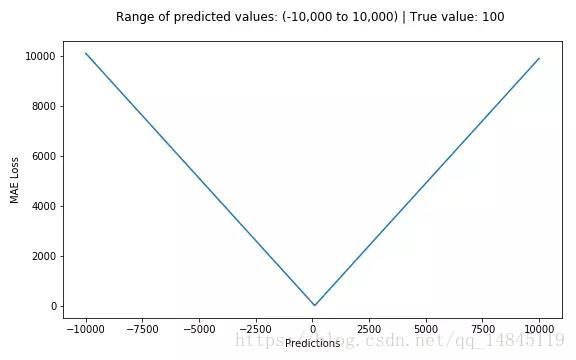
mean_squared_error(y_true, y_pred)

平均绝对误差meanabsolute error(MAE )和L1范数:

MAE表示了预测值与目标值之间差值的绝对值然后求平均

L1表示了预测值与目标值之间差值的绝对值，L1也叫做曼哈顿距离

MAE和L1的区别在于一个求了均值np.mean()，一个没有求np.sum()。2者的曲线走势也是完全一致的。

TensorFlow 接口：

tf.metrics.mean_absolute_error(labels,predictions,weights=None,metrics_collections=None,updates_collections=None,name=None
)

keras 接口：

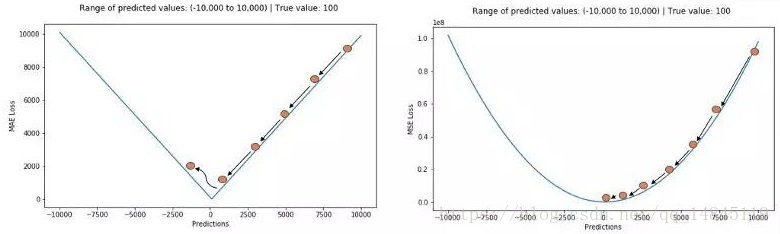
mean_absolute_error(y_true, y_pred)

MSE，MAE对比：

MAE损失对于局外点更鲁棒，但它的导数不连续使得寻找最优解的过程低效；MSE损失对于局外点敏感，但在优化过程中更为稳定和准确。

ID	Error	\|Error\|	Error2
1	0	0	0
2	1	1	1
3	-2	2	4
4	-0.5	0.5	0.25
5	1.5	1.5	2.25

MAE:1. RMSE:1.22

ID	Error	\|Error\|	Error2
1	0	0	0
2	1	1	1
3	1	1	1
4	-2	2	4
5	15	15	225

MAE. 3.8. RMSE:6.79

MSE易求解，但对异常值敏感，得到观测值的均值
MAE对于异常值更加稳健，得到观测值的中值

对于误差较大的异常样本，MSE损失远大于MAE，使用MSE的话，模型会给予异常值更大的权重，全力减小异常值造成的误差，导致模型整体表现下降。因此，训练数据中异常值较多时，MAE较好。

但MAE在极值点梯度会发生跃迁，即使很小的损失也会造成较大的误差，为解决这一问题，可以在极值附近动态减小学习率

总结：

MAE对异常值更加鲁棒，但导数的不连续导致找最优解过程中低效

MSE对异常值敏感，但优化过程更加稳定和准确

问题：

例如某个任务中90%的数据都符合目标值——150，而其余的10%数据取值则在0-30之间，那么利用MAE优化的模型将会得到150的预测值而忽略的剩下的10%（倾向于中值）；

而对于MSE来说由于异常值会带来很大的损失，将使得模型倾向于在0-30的方向取值。

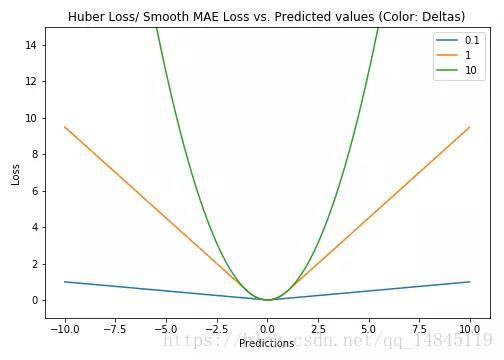
Huber Loss和smooth L1：

Huber loss具备了MAE和MSE各自的优点，当δ趋向于0时它就退化成了MAE,而当δ趋向于无穷时则退化为了MSE。

Smooth L1 loss也具备了L1 loss和L2 loss各自的优点，本质就是L1和L2的组合。

Huber loss和Smooth L1 loss具有相同的曲线走势，当Huber loss中的δ等于1时，Huber loss等价于Smooth L1 loss。

对于Huber损失来说，δ的选择十分重要，它决定了模型处理局外点的行为。当残差大于δ时使用L1损失，很小时则使用更为合适的L2损失来进行优化。

Huber损失函数克服了MAE和MSE的缺点，不仅可以保持损失函数具有连续的导数，同时可以利用MSE梯度随误差减小的特性来得到更精确的最小值，也对局外点具有更好的鲁棒性。

但Huber损失函数的良好表现得益于精心训练的超参数δ。

TensorFlow接口：

tf.losses.huber_loss(labels,predictions,weights=1.0,delta=1.0,scope=None,loss_collection=tf.GraphKeys.LOSSES,reduction=Reduction.SUM_BY_NONZERO_WEIGHTS
)

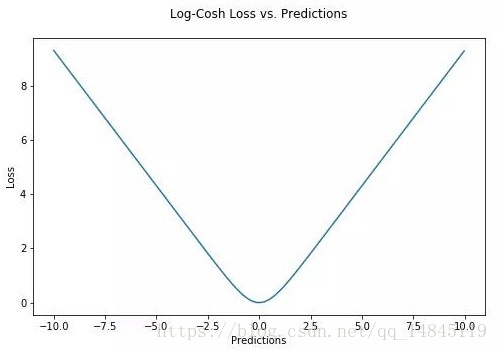
对数双曲余弦logcosh: