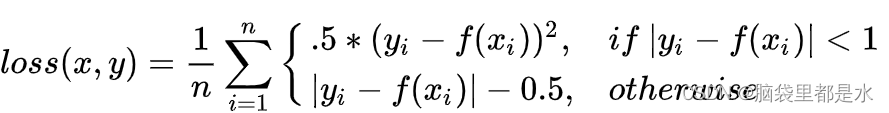如果我们定义了一个机器学习模型，比如一个三层的神经网络，那么就需要使得这个模型能够尽可能拟合所提供的训练数据。但是我们如何评价模型对于数据的拟合是否足够呢？那就需要使用相应的指标来评价它的拟合程度，所使用到的函数就称为损失函数(Loss Function)，当损失函数值下降，我们就认为模型在拟合的路上又前进了一步。最终模型对训练数据集拟合的最好的情况是在损失函数值最小的时候，在指定数据集上时，为损失函数的平均值最小的时候。

交叉熵损失函数（Cross Entropy）

在物理学中，“熵”被用来表示热力学系统所呈现的无序程度。香农将这一概念引入信息论领域，提出了“信息熵”概念，通过对数函数来测量信息的不确定性。

交叉熵（cross entropy）是信息论中的重要概念，主要用来度量两个概率分布间的差异。假定 $p$ 和 $q$ 是数据 $x$ 的两个概率分布，通过 $q$ 来表示 $p$ 的交叉熵可如下计算：$$H(p,q)=-\sum _{x}p(x)\log q(x))$$交叉熵刻画了两个概率分布之间的距离，旨在描绘通过概率分布 $q$ 来表达概率分布 $p$ 的困难程度。根据公式不难理解，交叉熵越小，两个概率分布 $p$ 和 $q$ 越接近。

这里仍然以三类分类问题为例，假设数据 $x$ 属于类别 1。记数据 $x$ 的类别分布概率为 $y$，显然 $y=(1,0,0)$代表数据 $x$ 的实际类别分布概率。记 $\hat{y}$ 代表模型预测所得类别分布概率。

那么对于数据 $x$ 而言，其实际类别分布概率 $y$ 和模型预测类别分布概率 $\hat{y}$ 的交叉熵损失函数定义为：
$$crossentropy=-y\times \log \left(\hat{y}\right)$$

很显然，一个良好的神经网络要尽量保证对于每一个输入数据，神经网络所预测类别分布概率与实际类别分布概率之间的差距越小越好，即交叉熵越小越好。于是，可将交叉熵作为损失函数来训练神经网络。

上图给出了一个三个类别分类的例子。由于输入数据 $x$ 属于类别 1，因此其实际类别概率分布值为 $y=(y_1,y_2,y_3)=(1,0,0)$。经过神经网络的变换，得到了输入数据 $x$ 相对于三个类别的预测中间值 $(z_1,z_2,z_3)$。然后，经过 Softmax 函数映射，得到神经网络所预测的输入数据 $x$ 的类别分布概率 $\hat{y}=({\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3)$。根据前面的介绍，${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3$为 (0,1) 范围之间的一个概率值。由于样本 $x$ 属于第一个类别，因此希望神经网络所预测得到的 ${\hat{y}}_1$取值要远远大于 ${\hat{y}}_2$ 和 ${\hat{y}}_3$ 的取值。为了得到这样的神经网络，在训练中可利用如下交叉熵损失函数来对模型参数进行优化：$$crossentropy=-\left(y_1\times \log \left({\hat{y}}_1\right)+y_2\times \log \left({\hat{y}}_2\right)+y_3\times \log \left({\hat{y}}_3\right)\right)$$在上式中，$y_2$ 和 $y_3$ 均为 0、$y_1$ 为 1，因此交叉熵损失函数简化为：$$-y_1\times \log \left({\hat{y}}_1\right)=-\log \left({\hat{y}}_1\right)$$在神经网络训练中，要将输入数据实际的类别概率分布与模型预测的类别概率分布之间的误差（即损失）从输出端向输入端传递，以便来优化模型参数。下面简单介绍根据交叉熵计算得到的误差从 ${\hat{y}}_1$ 传递给 $z_1$ 和 $z_2$（$z_3$ 的推导与 $z_2$ 相同）的情况。$$\frac{\partial {\hat{y}}_1}{\partial z_1}=\frac{\partial \left(\frac{e^{z_1}}{{\sum }_k{e}^{z_k}}\right)}{\partial z_1}=\frac{{\left(e^{z_1}\right)}^{{}^{\prime }}\times {\sum }_k{e}^{z_k}-e^{z_1}\times e^{z_1}}{{\left({\sum }_k{e}^{z_k}\right)}^2}=\frac{e^{z_1}}{{\sum }_k{e}^{z_k}}-\frac{e^{z_1}}{{\sum }_k{e}^{z_k}}\times \frac{e^{z_1}}{{\sum }_k{e}^{z_k}}={\hat{y}}_1\left(1-{\hat{y}}_1\right)$$由于交叉熵损失函数 $-\log \left({\hat{y}}_1\right)$ 对 ${\hat{y}}_1$ 求导的结果为 $-\frac{1}{{\hat{y}}_1}$，${\hat{y}}_1\left(1-{\hat{y}}_1\right)$ 与 $-\frac{1}{{\hat{y}}_1}$ 相乘的结果为 ${\hat{y}}_1-1$ 这说明一旦得到模型预测输出 ${\hat{y}}_1$，将该输出减去1就是交叉损失函数相对于 $z_1$ 的偏导结果。$$\frac{\partial {\hat{y}}_1}{\partial z_2}=\frac{\partial \left(\frac{e^{z_1}}{{\sum }_k{e}^{z_k}}\right)}{\partial z_2}=\frac{0\times {\sum }_k{e}^{z_k}-e^{z_1}\times e^{z_2}}{{\left({\sum }_k{e}^{z_k}\right)}^2}=-\frac{e^{z_1}}{{\sum }_k{e}^{z_k}}\times \frac{e^{z_2}}{{\sum }_k{e}^{z_k}}=-{\hat{y}}_1{\hat{y}}_2$$同理，交叉熵损失函数导数为 $-\frac{1}{{\hat{y}}_1}$，$-{\hat{y}}_1{\hat{y}}_2$ 与 $-\frac{1}{{\hat{y}}_1}$ 相乘结果为 ${\hat{y}}_2$。这意味对于除第一个输出节点以外的节点进行偏导，在得到模型预测输出后，只要将其保存，就是交叉损失函数相对于其他节点的偏导结果。在 $z_1$、$z_2$ 和 $z_3$得到偏导结果后，再通过链式法则（后续介绍）将损失误差继续往输入端传递即可。

在上面的例子中，假设所预测中间值 $(z_1,z_2,z_3)$ 经过 Softmax 映射后所得结果为 $(0.34,0.46,0.20)$。由于已知输入数据 $x$ 属于第一类，显然这个输出不理想而需要对模型参数进行优化。如果选择交叉熵损失函数来优化模型，则 $(z_1,z_2,z_3)$ 这一层的偏导值为 $(0.34-1,0.46,0.20)=(-0.66,0.46,0.20)$。

可以看出，Softmax 和交叉熵损失函数相互结合，为偏导计算带来了极大便利。偏导计算使得损失误差从输出端向输入端传递，来对模型参数进行优化。在这里，交叉熵与 Softmax 函数结合在一起，因此也叫 Softmax 损失（Softmax with cross-entropy loss）。

均方差损失（Mean Square Error，MSE）

均方误差损失又称为二次损失、L2损失，常用于回归预测任务中。均方误差函数通过计算预测值和实际值之间距离（即误差）的平方来衡量模型优劣。即预测值和真实值越接近，两者的均方差就越小。

假设有 $n$ 个训练数据 $x_i$，每个训练数据 $x_i$ 的真实输出为 $y_i$，模型对 $x_i$ 的预测值为 ${\hat{y}}_i$。该模型在 $n$ 个训练数据下所产生的均方误差损失可定义如下：$$MSE=\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2$$假设真实目标值为100，预测值在 -10000 到 10000 之间，绘制MSE函数曲线如下图所示。可以看到，当预测值越接近100时，MSE损失值越小。MSE损失的范围为 0 到 $\infty$ 。