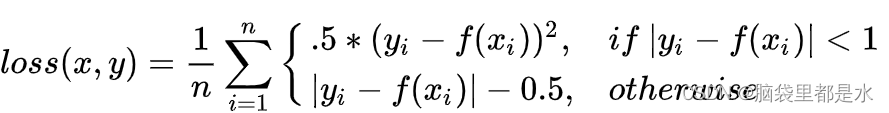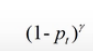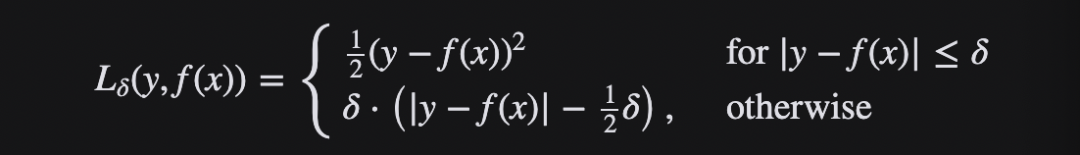深度学习——损失函数（Regression Loss、Classification Loss）

article/2025/10/28 10:54:12

简介

Loss function

损失函数

用于定义单个训练样本与真实值之间的误差

Cost function

代价函数

用于定义单个批次/整个训练集样本与真实值之间的误差

Objective function

目标函数

泛指任意可以被优化的函数

损失函数用于衡量模型所做出的预测离真实值(GT)之间的偏离程度。

损失函数分为两种：回归损失（针对连续型变量）和分类损失（针对离散型变量）

知道每一种损失函数的优点和局限性，才能更好的利用它们去解决实际问题

回归损失(Regression Loss)

L1 Loss

也称为Mean Absolute Error，即平均绝对误差(MAE)，它衡量的是预测值与真实值之间的距离的平均误差幅度。

作用范围：0到正无穷。

公式如下：（N个样本，M个类别）

$L_{l1 \space loss} = \frac{1}{N} \sum^{N}_{i=1} \sum^{M}_{t=1} |y_t^i - \hat{y}_t^i|$

优点：收敛速度快，能够对梯度给予合适的惩罚权重，使梯度更新的方向可以更加精确。

缺点：对异常值敏感，梯度更新的方向很容易受离群点所主导，不具备鲁棒性。

L2 Loss

也称为Mean Squared Error，即均方差(MSE)，它衡量的是预测值与真实值之间距离的平方和。

作用范围：0到正无穷。

公式如下：（N个样本，M个类别）

$L_{l2 \space loss} = \frac{1}{N} \sum^{N}_{i=1} \sum^{M}_{t=1} (y_t^i - \hat{y}_t^i)^2$

优点：对离群点(outliers)或者异常值更具有鲁棒性。

缺点：

在0点处的导数不连续，使得求解效率低下，导致收敛速度慢
对于较小的损失值，其梯度也与其他区间损失值的梯度一样大，不利于网络学习

异常值对于实际业务非常重要，可使用MSE作为损失函数

异常值仅仅表示损坏的数据，可使用MAE作为损失函数

Smooth L1 Loss

出自 Fast RCNN

综合L1和L2损失的优点，在0点处附近采用了L2损失中的平方函数，解决了L1损失在0点处梯度不可导的问题，使其更加平滑易于收敛。

公式如下：

$smooth_{L1}(x) = \begin{cases} 0.5x^2 &\text{if } |x|<1 \\ |x|-0.5 &\text{otherwise} \end{cases}$

IoU Loss

出自 UnitBox

常规的Lx损失中，都是基于目标边界中的4个坐标点信息之间分别进行回归损失计算，因此，这些边框信息之间相互独立。

IoU损失将候选框的四个边界信息作为一个整体进行回归，从而实现准确、高效的定位，具有很好的尺度不变性。

为了解决IoU度量不可导的现象，引入了负Ln范数来间接计算IoU损失。

$Ground \space truth: \hat{x} = (\hat{x}_t, \hat{x}_b, \hat{x}_l, \hat{x}_r) \\ Prediction: x = (x_t, x_b, x_l, x_r) \\ IoU \space Loss = - \ln{\frac{Intersection(Ground \space truth, Prediction)}{Union(Ground \space truth, Prediction)}}$

GIoU Loss

出自 Generalized Intersection over Union

$A,B, the \space smallest \space encolsing \space convex \space object \space C \\ IoU = \frac{|A \cap B|}{|A \cup B|} \\ GIoU = IoU - \frac{|C-(A \cup B)|}{|C|} \\ L_{GIoU} = 1- GIoU$

分类损失(Classification Loss)

Cross Entropy Loss

其中y_i为真实值，p_i为该类别的预测值（对单个样本）

$L(y,p) = -\sum_{i}{y_i \cdot \log{p_i}}$

Focal Loss

出自 Focal Loss for Dense Object Detection

出发点：解决one-stage算法不如two-stage算法准确率高的问题。

主要原因：样本的类别不均衡（比如前景和背景）

比如在很多输入图片中，我们利用网格去划分小窗口，大多数的窗口是不包含目标的。

直接运用原始的交叉熵损失，那么负样本所占比例会非常大，主导梯度的优化方向，即网络会偏向于将前景预测为背景。即使使用OHEM（在线困难样本挖掘）算法来处理不均衡的问题，虽然其增加了误分类样本的权重，但也容易忽略掉易分类样本。

解决方案：Focal loss聚焦于训练一个困难样本的稀疏集，通过直接在标准的交叉熵损失函数基础上做改进，引进了两个惩罚因子，来减少易分类样本的权重，使得模型在训练过程中更专注于困难样本。

$FL(p, \hat{p}) = -(\alpha (1-\hat{p})^{\gamma} p\log{\hat{p}} + (1-\alpha)\hat{p}^{\gamma}(1-p)\log{(1-\hat{p})})$