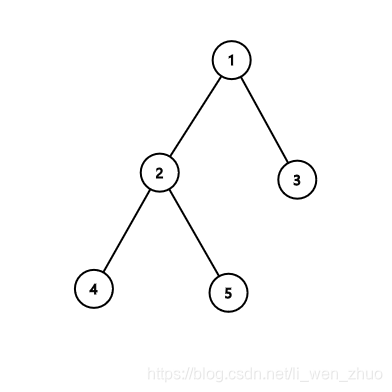
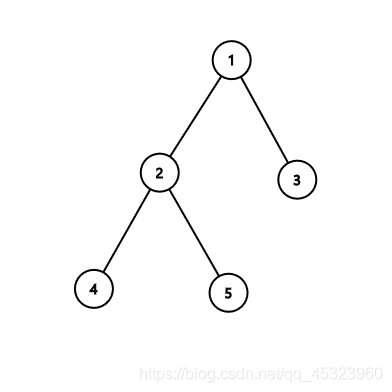
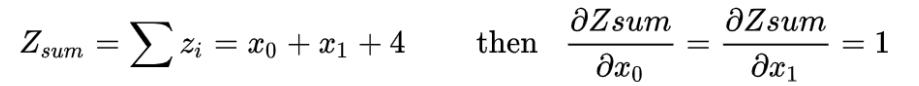$树边:$深度优先森林中的边。如果结点v是因对(u,v)的探索而首先被发现,则(u,v)是一条树边。
$后向边:$后向边(u,v)是将结点u连接到其在深度优先树中一个祖先节点v的边.
（本文我就称之为反向边了，问题不大）
$前向边:$是将结点u连接到其在深度优先树中一个后代结点v的边(u,v).
$横向边:$指其他所有的边,这些边可以连接同一颗深度优先树中的结点，只要其中一个结点不是另外一个结点的祖先,也可以连接不同深度优先树的两个结点。

其实就是找出无向图中的简单环(不含重边,环内部非相邻点之间没有边)
你找到一个长度大于k的环，直接取不相邻的间隔点按情况1处理即可。
找到长度小于k的环，直接可作为结果按情况2输出。
没找到简单环的情况，就说明这是一颗树，按深度奇偶性分成两部分,取元素多的那一部分按情况一处理。

那么怎么在无向图中找环呢?
其实找到一条指向祖先节点的反向边即可。
如果存在这么一条反向边，那么更新，取深度较大的点连成环(和深度小的点成环有可能环中存在更小的环，即不是简单环)

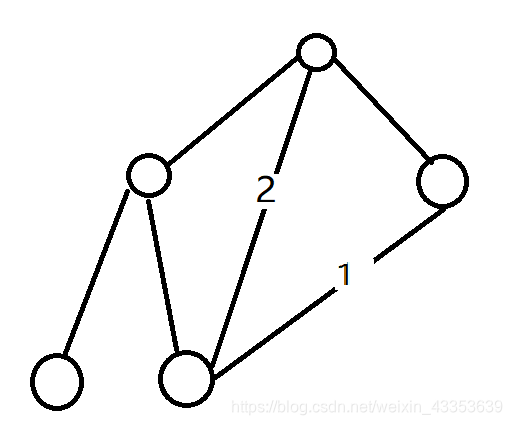
可以假定图中的深度优先森林有1,2两条不符合树定义的边，2是反向边，与非祖先节点连接的1这条边则是横向边。但我们在深度优先遍历找环的过程中其实是不会碰到横向边的,（如果有这条边，也己经成为了树边）。所以怎么利用这个性质呢?可以发现我在深度遍历过程中用到了一个随放随扔的vector,它可以维护根节点到当前点的路径。那么如果找到一个点深度比当前点小于1以上,即可表示从该点到当前可以连接成环(不一定是简单环),我们取max的作用就是为了防止取到的是一个非简单环，取完max就可以保证简单环了.

 for(auto it:e[x]){if(dep[it]){if(dep[x]-dep[it]>1){flag=max(dep[it],flag);}}}

然后这里dfs中在当前点找环和进行子树遍历的顺序也很重要,一定要优先在当前节点找环,之后才进行子树的判定.不然也可能会出现非简单环的情况。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define MAXN 500005
#define rep(n) for(int i=1;i<=n;i++)
#define rall(x) for(int i=(x).size()-1;i>=0;i--)
#define all(x) for(int i=0;i<(x).size();i++)
vector<int>e[MAXN];
int dep[MAXN];
vector<int>sta;
vector<int>ans;
int n,m,k;
vector<int>col[2];
void dfs(int x)
{if(ans.size())return;col[dep[x]%2].push_back(x);sta.push_back(x);int flag=-1;for(auto it:e[x]){if(dep[it]){if(dep[x]-dep[it]>1){flag=max(dep[it],flag);}}}if(flag!=-1){for(int i=flag;i<=dep[x];i++)ans.push_back(sta[i-1]);return ;}for(auto it:e[x]){if(!dep[it]){dep[it]=dep[x]+1;dfs(it);}}sta.pop_back();}
int main()
{scanf("%d%d%d",&n,&m,&k);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);e[v].push_back(u);e[u].push_back(v);}dep[1]=1;dfs(1);if(ans.size()==0){if(col[0].size()<col[1].size())swap(col[0],col[1]);for(int i=0;i<(k+1)/2;i++)ans.push_back(col[0][i]);printf("1\n");} else{vector<int>tmp;if(ans.size()>k){printf("1\n");for(int i=0;i<(k+1)/2;i++)tmp.push_back(ans[2*i]);ans.assign(tmp.begin(),tmp.end());}else{printf("2\n%d\n",ans.size());}}for(auto it:ans){if(it!=*ans.begin())putchar(' ');printf("%d",it);}
}