CodeForces - 1364D Ehabs Last Corollary(dfs树找最小环)

article/2025/10/28 13:21:48

题目链接：点击查看

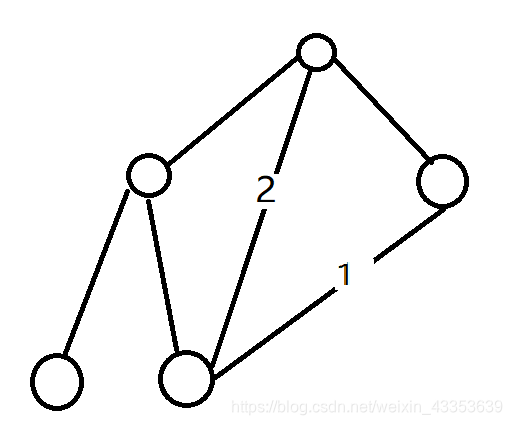
题目大意：给出一个由 n 个结点和 m 条边构成的无向图，再给出一个 k ，需要在图中完成下面任意一种操作：

找到一个大小恰好为 $\left \lceil \frac{k}{2} \right \rceil$ 的独立集
找到一个大小不超过 k 的环

题目分析：

题目已经提示了题目一定有解，所以首先证明一下可行性：

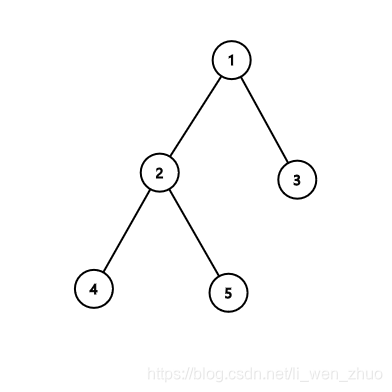
对于一个连通图，如果是树的话，可以按照深度划分，同奇偶的深度是可以构成独立集的，所以一定存在 $\left \lceil \frac{k}{2} \right \rceil$ 大小的独立集

如果不是树的话，那么一定存在环，我们假设其最小环的长度为 mmin ，如果 mmin <= k，则显然满足条件 2 ，直接输出即可

如果最小环的长度 mmin > k 的话，因为在一个环上，相隔的点肯定是可以构成独立集的，而一个长度为 mmin 的环最多可以构成 $\left \lceil \frac{mmin}{2} \right \rceil$ 大小的独立集，因为 mmin > k，所以 $\left \lceil \frac{mmin}{2} \right \rceil>\left \lceil \frac{k}{2} \right \rceil$ ，一定存在一个大小为 $\left \lceil \frac{k}{2} \right \rceil$ 的独立集，证毕

这样一来，对于树我们单独实现，直接dfs跑深度然后分类，对于非树我们可以在dfs树上找最小环，然后再分类讨论就好了，为了方便处理，直接令 deep 深度数组代替 vis 标记数组，并且额外维护一个 pre 数组记录一下每个点的父节点，方便记录环的路径

代码：

#include<iostream>
#include<cstdio>
#include<string>
#include<ctime>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<stack>
#include<climits>
#include<queue>
#include<map>
#include<set>
#include<sstream>
#include<cassert>
using namespace std;typedef long long LL;typedef unsigned long long ull;const LL inf=0x3f3f3f3f;const int N=2e5+100;int n,m,k,mmin=inf,pos=-1,deep[N],pre[N];vector<int>node[N];vector<int>p[2];void DFS(int u,int fa,int dep)//树的dfs 
{p[dep%2].push_back(u);for(auto v:node[u]){if(v==fa)continue;DFS(v,u,(dep+1)%2);}
}void dfs(int u,int fa,int dep)//非树的dfs
{deep[u]=dep;pre[u]=fa;for(auto v:node[u]){if(v==fa)continue;if(deep[v]!=0){if(deep[u]-deep[v]+1>=0&&mmin>deep[u]-deep[v]+1){mmin=deep[u]-deep[v]+1;pos=u;}}elsedfs(v,u,dep+1);}
}int main()
{
#ifndef ONLINE_JUDGE
//  freopen("input.txt","r",stdin);
//  freopen("output.txt","w",stdout);
#endif
//  ios::sync_with_stdio(false);scanf("%d%d%d",&n,&m,&k);for(int i=1;i<=m;i++){int u,v;scanf("%d%d",&u,&v);node[u].push_back(v);node[v].push_back(u);}if(m==n-1)//树{DFS(1,-1,0);if(p[0].size()<p[1].size())swap(p[0],p[1]);puts("1");for(int i=0;i<(k+1)/2;i++)printf("%d ",p[0][i]);}else//非树{dfs(1,-1,1);if(mmin<=k){puts("2");printf("%d\n",mmin);while(mmin--){printf("%d ",pos);pos=pre[pos];}}else{puts("1");int num=(k+1)/2;while(num--){printf("%d ",pos);pos=pre[pos];pos=pre[pos];}}}return 0;
}