参数检验-显著性等数据分析前，如何用R语言完成。首先考虑数据的独立性（卡方检验、Fisher检验、Cochran-Mantel-Haenszel检验），其次检验数据的正态性（shapiro.test) or (qqnorm）等和方差齐性（bartlett.test) or (leveneTest）。因为统计学中的t检验和方差分析等方法，必要条件是样本都来自正态或近似正态分布，只有符合条件，才能用该方法进一步检验各样本所属的总体参数的显著性差异；否则要改换其他非参数的方法进行检验。

检验数据独立性的方法

对于数据的独立性，除特殊情况外，一般情况下是默认符合的。当然，如果实在不放心，也可以利用独立性检验算法，主要方法有：卡方检验、Fisher检验、Cochran-Mantel-Haenszel检验。话不多说，直接上代码：

Chisq检验

# install.packages("vcd")
library(vcd) # 加载该R包主要是为了利用Arthritis这个数据集 （该R包自带的数据集）
#1
mytable1 <- table(Arthritis$Treatment,Arthritis$Improved)
chisq.test(mytable1)
#2
mytable2 <- table(Arthritis$Sex,Arthritis$Improved)
chisq.test(mytable2)

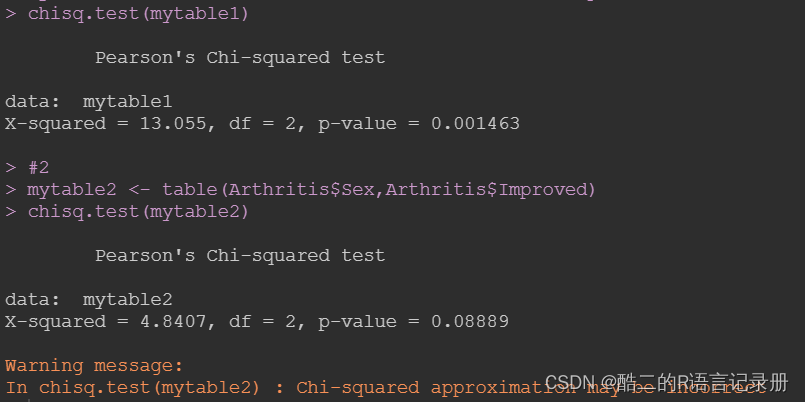
1.chisq.test函数中的参数p默认每个量的概率是1/length(mytable1)，即所有概率都相等，是独立的。在这种情况下，检验的假设是总体概率是否等于p中的概率。这里结果是p-value值小于0.05，即Treatment与Improved是相关的，不是独立的；2.结果显示p-value值大于0.05，即Sex与Improved是独立不相关的，也就是药物没有性别差异。

Fisher检验

该方法的原理是边际固定的列联表中行和列是相互独立的。

#1
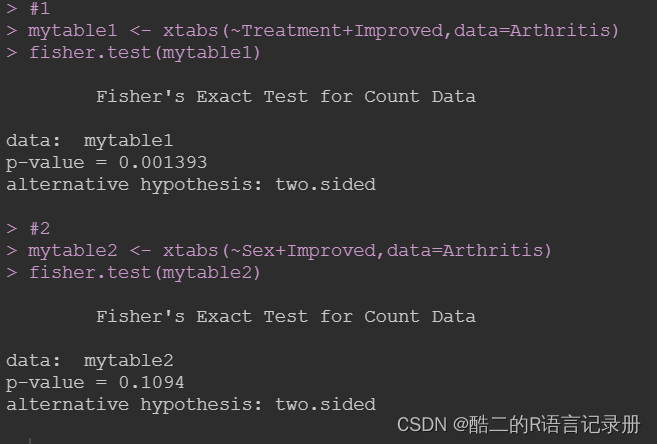
mytable1 <- xtabs(~Treatment+Improved,data=Arthritis)
fisher.test(mytable1)
#2
mytable2 <- xtabs(~Sex+Improved,data=Arthritis)
fisher.test(mytable2)

与上述结果相似，不再赘述

Cochran-Mantel-Haenszel检验

该检验方法的原理：两个名义变量在第三个变量每一个水平中都是独立的。因此，该检验方法需要三个变量。

mytable <- xtabs(~Treatment+Improved+Sex,Arthritis)
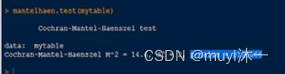
mantelhaen.test(mytable)

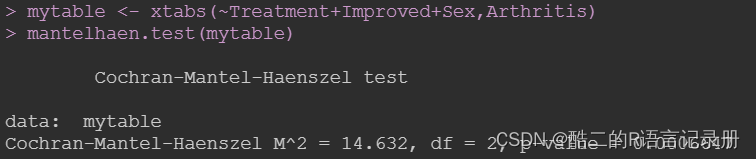
p-value值非常小，说明药物治疗和改善情况在性别的每一个水平上不独立。需要注意的是，这里函数中的变量顺序很重要。

检验数据正态性的方法

主要的函数：shapiro.test、qqnorm、ksnormTest、lillie.test以及特殊的ks.test，以上几种函数都可以用于检验数据是否满足正态性。

• H0: 样本所来自的总体分布服从正态分布，检验结果的 p-value > 0.05数据就是满足正态分布。

shapiro.test函数

注意 此种方法能够检验的样本大小必须在3和5000之间

set.seed(1);x <- rnorm(450) # 分号表示连续读取命令，rnorm表示生成符合正态分布的数值
shapiro.test(x) # 检验数据是否符合正态性
shapiro.test(runif(100, min = 2, max = 4)) # runif随机生成对应数量的数值，并直接检验其是否满足正态性

1.根据结果p-value > 0.05 ，接受原假设，即认为数据满足正态分布。
2.根据结果p-value < 0.05 ，拒绝原假设，即认为数据不满足正态分布。

qqnorm函数

主要是用于判断数据是否偏离正态分布的趋势线距离的一种图–QQ图

set.seed(1);x <- rnorm(450)
qqnorm(x);qqline(x) # 绘制qq图及添加趋势线来判断set.seed(2);x1 <- runif(100, min = 2, max = 4)
qqnorm(x1);qqline(x1)

1.第一种结果与上面shapiro.test函数得到的结果类似，数据基本位于趋势线上。

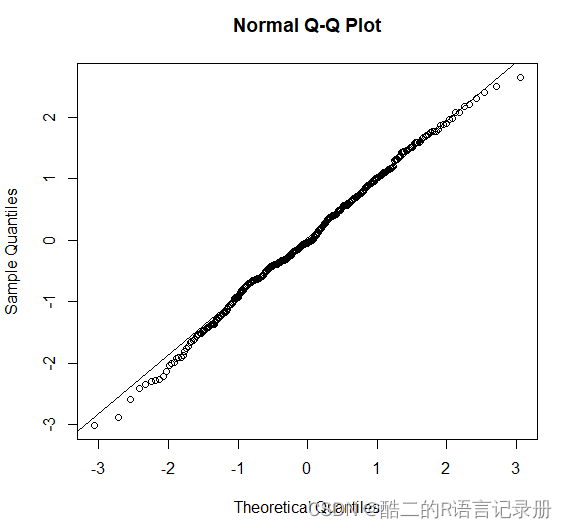
2.我们可以从图中看出，两端的值都偏离了，因此数据不太满足正态性。

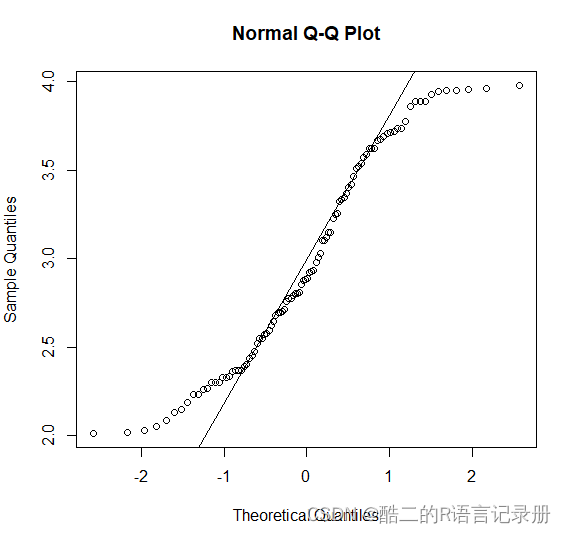
ksnormTest函数

# install.packages("fBasics")
set.seed(1);x <- rnorm(450)
set.seed(2);x1 <- runif(100, min = 2, max = 4)
library(fBasics)
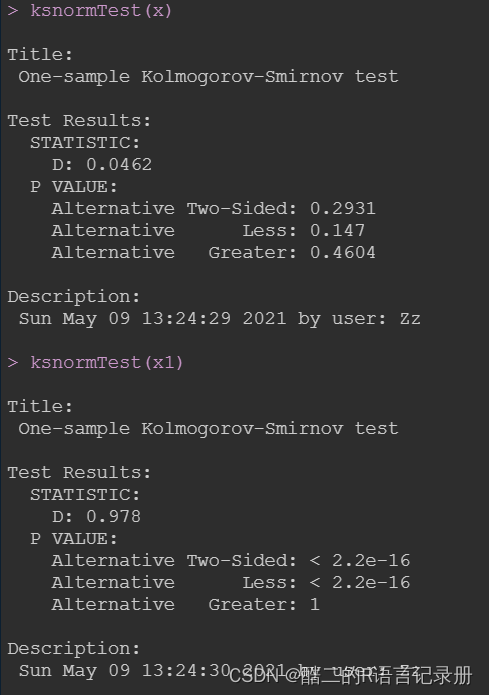
ksnormTest(x)
ksnormTest(x1)

得到结果，与方法一的结果一致

lillie.test函数

# install.packages("nortest")
set.seed(1);x <- rnorm(450)
set.seed(2);x1 <- runif(100, min = 2, max = 4)
library(nortest)
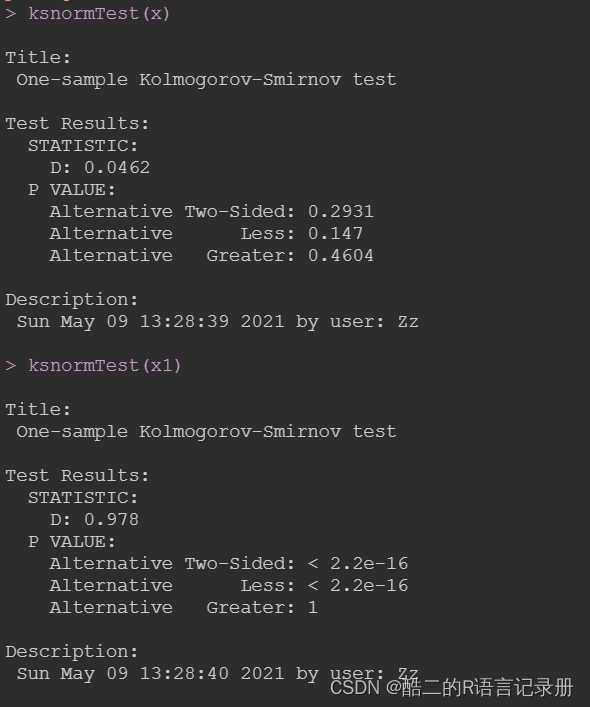
ksnormTest(x)
ksnormTest(x1)

ks.test函数

K-S检验检验单一样本是否来自某一特定分布。比如检验一组数据是否为正态分布。它的检验方法是以样本数据的累积频数分布与特定理论分布比较，若两者间的差距很小，则推论该样本取自某特定分布族。K-S检验的原假设和备择假设为：

• H0: 样本所来自的总体分布服从某特定分布
• H1: 样本所来自的总体分布不服从某特定分布

如果要检验数据是否满足正态分布，只要把特定分布设定为“正态分布”即可。用R语言进行K-S检验的代码如下：

set.seed(1);x <- rnorm(450)
set.seed(2);x1 <- runif(100, min = 2, max = 4)
ks.test(x,"pnorm") # norm表示正态分布，p表示概率
ks.test(x1,"pnorm")

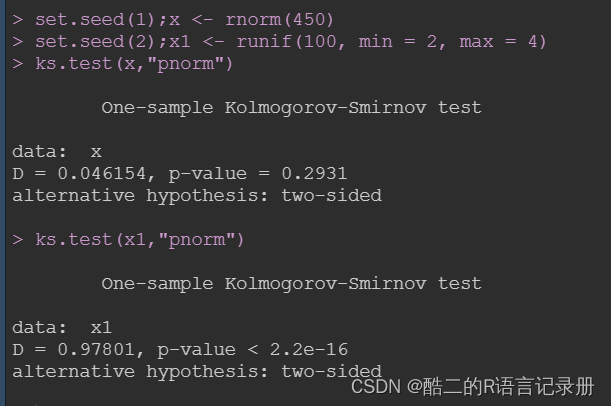
1.根据结果p-value > 0.05，接受原假设，即认为x数据满足正态分布。
2.根据结果p-value < 0.05 ，拒绝原假设，即认为x1数据不满足正态分布。

Tips:

• 大样本、已知总体均数和标准差，选择非参数检验-单样本KS检验比较好
• 单样本K-S检验要求检验分布是连续的，而连续分布出现相同值的概率为0.如果是出现相同的，则连续分布的假设不成立，则该方法无法使用

方差齐性检验的方法

对于数据的方差齐性检验，通常可以使用bartlett.test()、及car包中的leveneTest()函数来进行。

bartlett.test()检验

该检验主要适用于正态分布数据

require(graphics)
# 对于单一变量
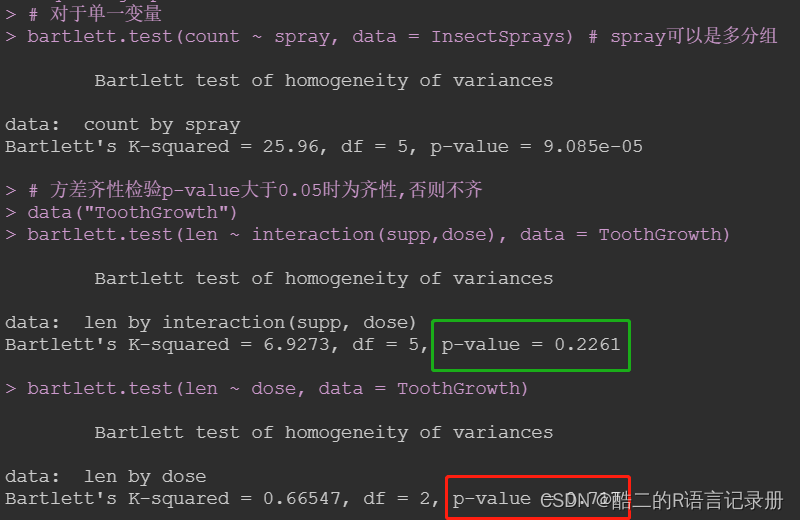
bartlett.test(count ~ spray, data = InsectSprays) # spray可以是多分组
# 方差齐性检验p-value大于0.05时为齐性,否则不齐# 对于多变量
data("ToothGrowth")
bartlett.test(len ~ interaction(supp,dose), data = ToothGrowth)
bartlett.test(len ~ dose, data = ToothGrowth)

Tips：对于有多个自变量的情况，我们需要运用interaction()函数来将多个自变量折叠为一个单一的变量用于表示不同变量因素之间的组合。如果不这么做的话，检验的自由度将会发生错误，进而导致我们得到错误的p值。

leveneTest ()检验

非正态分布与正态分布数据均适用

# install.packages("car")
library(car)
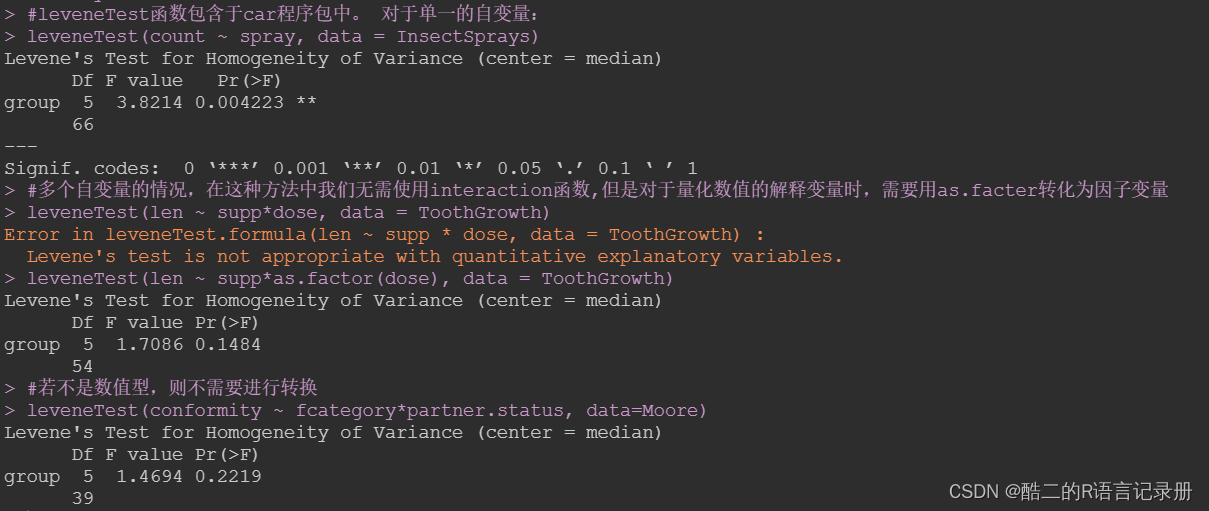
#leveneTest函数包含于car程序包中。对于单一的自变量：
leveneTest(count ~ spray, data = InsectSprays)
#多个自变量的情况，在这种方法中我们无需使用interaction函数,但是对于量化数值的解释变量时，需要用as.facter转化为因子变量
leveneTest(len ~ supp*dose, data = ToothGrowth)
leveneTest(len ~ supp*as.factor(dose), data = ToothGrowth)
#若不是数值型，则不需要进行转换
leveneTest(conformity ~ fcategory*partner.status, data=Moore)

完整代码

####################################
#数据的独立性、正态性、方差齐性检验
####################################
#数据的独立性检验
# 卡方检验
# install.packages("vcd")
library(vcd)
#1
mytable1 <- table(Arthritis$Treatment,Arthritis$Improved)
chisq.test(mytable1)
#2
mytable2 <- table(Arthritis$Sex,Arthritis$Improved)
chisq.test(mytable2)# Fisher检验
#1
mytable1 <- xtabs(~Treatment+Improved,data=Arthritis)
fisher.test(mytable1)
#2
mytable2 <- xtabs(~Sex+Improved,data=Arthritis)
fisher.test(mytable2)# Cochran-Mantel-Haenszel检验
mytable <- xtabs(~Treatment+Improved+Sex,Arthritis)
mantelhaen.test(mytable)#数据正态性检验
# shapiro.test
set.seed(1);x <- rnorm(450)
shapiro.test(x)
shapiro.test(runif(100, min = 2, max = 4))# qqnorm
x <- rnorm(450)
qqnorm(x)；qqline(x)
set.seed(2);x1 <- runif(100, min = 2, max = 4)
qqnorm(x1);qqline(x1)# ksnormTest
# install.packages("fBasics")
set.seed(1);x <- rnorm(450)
set.seed(2);x1 <- runif(100, min = 2, max = 4)
library(fBasics)
ksnormTest(x)
ksnormTest(x1)# lillie.test
# install.packages("nortest")
set.seed(1);x <- rnorm(450)
set.seed(2);x1 <- runif(100, min = 2, max = 4)
library(nortest)
ksnormTest(x)
ksnormTest(x1)# 特殊的ks.test
set.seed(1);x <- rnorm(450)
set.seed(2);x1 <- runif(100, min = 2, max = 4)
ks.test(x,"pnorm")
ks.test(x1,"pnorm")#方差齐性检验
# bartlett.test()检验
require(graphics)
# 对于单一变量
bartlett.test(count ~ spray, data = InsectSprays) # spray可以是多分组
# 方差齐性检验p-value大于0.05时为齐性,否则不齐
data("ToothGrowth")
bartlett.test(len ~ interaction(supp,dose), data = ToothGrowth)
bartlett.test(len ~ dose, data = ToothGrowth)# leveneTest()检验
# install.packages("car")
library(car)
#leveneTest函数包含于car程序包中。对于单一的自变量：
leveneTest(count ~ spray, data = InsectSprays)
#多个自变量的情况，在这种方法中我们无需使用interaction函数,但是对于量化数值的解释变量时，需要用as.facter转化为因子变量
leveneTest(len ~ supp*dose, data = ToothGrowth)
leveneTest(len ~ supp*as.factor(dose), data = ToothGrowth)
#若不是数值型，则不需要进行转换
leveneTest(conformity ~ fcategory*partner.status, data=Moore)

参考链接：

1. https://blog.csdn.net/weixin_44384631/article/details/107575050
2. https://blog.csdn.net/u011253874/article/details/42683057