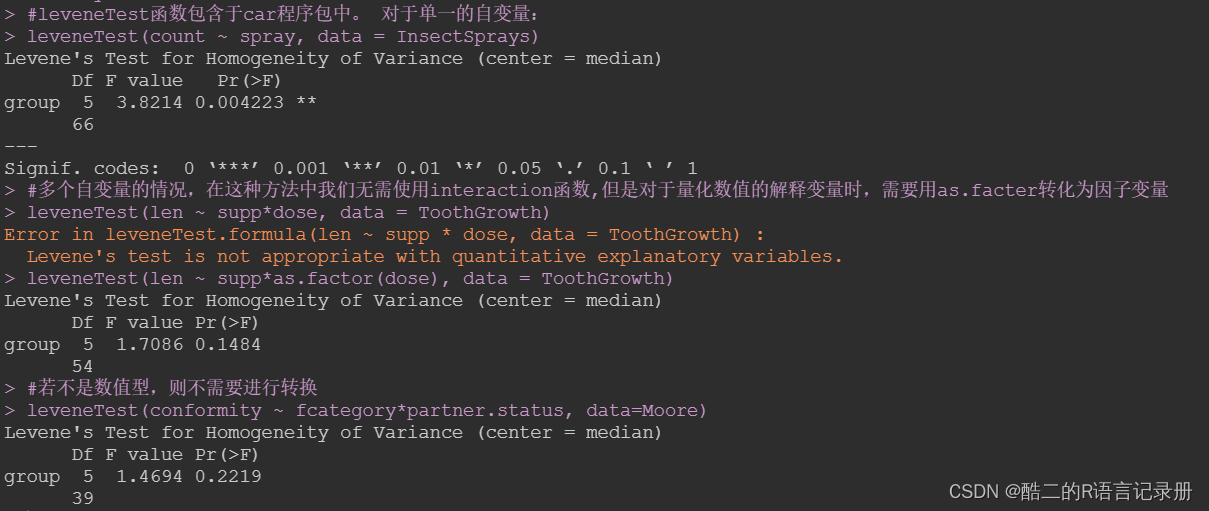
这里写目录标题
- 1、声明
- 2、机器学习评估性能指标
- 2.1、回归(Regression)算法指标
- 2.1.1、平均绝对误差 MAE
- 2.1.2、均方误差 MSE
- 2.1.3、均方根误差 RMSE
- 2.1.4、决定系数R^2
- 2.1.5、解决评估指标鲁棒性问题
- 2.2、分类(Classification)算法指标
- 2.2.1、精度 ACC
- 2.2.2、混淆矩阵Confusion Matrix
- 2.2.3、准确率(查准率) Precision
- 2.2.4、召回率(查全率)Recall
- 2.2.5、Fβ Score
- 2.2.6、ROC 和 AUC
- 2.2.7、KS Kolmogorov-Smirnov
- 3、深度学习目标检测评估性能指标
- 3.1、一个例子---Precision和Recall
- 3.2、如何评判检测器的好坏?
- 3.3、常用性能指标
- 3.3.1、PR曲线
- 3.3.2、mAP
- 3.3.3、fppi/fppw
- 3.4、其余指标
- 3.4.1、速度指标
- 3.4.2、内存指标
- 4、结尾
1、声明
本文基于以下两篇文章合并而来,主要针对机器学习和深度学习的评价性能指标进行阐述。
链接:
[1] 机器学习评估指标.
[2] 白裳.
如果觉得好的话,请也去原作者那里点个赞!
2、机器学习评估性能指标
2.1、回归(Regression)算法指标
- Mean Absolute Error 平均绝对误差
- Mean Squared Error 均方误差
- Mean Squared Error 均方误差
- Coefficient of determination 决定系数
以下为一元变量和二元变量的线性回归示意图:

怎样来衡量回归模型的好坏呢? 我们第一眼自然而然会想到采用残差(实际值与预测值差值)的均值来衡量,即:
r e s i d u a l ( y , y ^ ) = 1 m ∑ i = 1 m ( y i − y ^ i ) residual(y,\hat y) = \frac{1}{m}\sum\limits_{i = 1}^m {({y_i} - {{\hat y}_i})} residual(y,y^)=m1i=1∑m(yi−y^i)
问题 1:用残差的均值合理吗?
当实际值分布在拟合曲线两侧时,对于不同样本而言,有正有负,相互抵消,因此我们想到采用预测值和真实值之间的距离来衡量。
2.1.1、平均绝对误差 MAE
平均绝对误差MAE(Mean Absolute Error)又被称为 L1范数损失,公式如下:
M A E ( y , y ^ ) = 1 m ∑ i = 1 m ∣ y i − y ^ i ∣ MAE(y,\hat y) = \frac{1}{m}\sum\limits_{i = 1}^m {\left| {{y_i} - {{\hat y}_i}} \right|} MAE(y,y^)=m1i=1∑m∣yi−y^i∣
问题 2:MAE有哪些不足?
MAE虽能较好衡量回归模型的好坏,但是绝对值的存在导致函数不光滑,在某些点上不能求导,可以考虑将绝对值改为残差的平方,这就是均方误差。
2.1.2、均方误差 MSE
均方误差MSE(Mean Squared Error)又被称为 L2范数损失,公式如下:
M S E ( y , y ^ ) = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 MSE(y,\hat y) = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} MSE(y,y^)=m1i=1∑m(yi−y^i)2
问题 3: 还有没有比MSE更合理一些的指标?
由于MSE与我们的目标变量的量纲不一致,为了保证量纲一致性,我们需要对MSE进行开方。
2.1.3、均方根误差 RMSE
R M S E ( y , y ^ ) = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 RMSE(y,\hat y) = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} } RMSE(y,y^)=m1i=1∑m(yi−y^i)2
问题 4: RMSE有没有不足的地方?有没有规范化(无量纲化的指标)?
上面的几种衡量标准的取值大小与具体的应用场景有关系,很难定义统一的规则来衡量模型的好坏。
比如说利用机器学习算法预测上海的房价RMSE在2000元,我们是可以接受的,但是当四五线城市的房价RMSE为2000元,我们还可以接受吗?下面介绍的决定系数就是一个无量纲化的指标。
2.1.4、决定系数R^2
变量之所以有价值,就是因为变量是变化的。什么意思呢?比如说一组因变量为[0, 0, 0, 0, 0],显然该因变量的结果是一个常数0,我们也没有必要建模对该因变量进行预测。假如一组的因变量为[1, 3, 7, 10, 12],该因变量是变化的,也就是有变异,因此需要通过建立回归模型进行预测。这里的变异可以理解为一组数据的方差不为0。
决定系数又称为R^2 score,反映因变量的全部变异能通过回归关系被自变量解释的比例,如下所示:
S S T = ∑ i = 1 m ( y i − y ˉ ) 2 S S T = t o t a l s u m o f s q u a r e s SST = \sum\limits_{i = 1}^m {{{\left( {{y_i} - \bar y} \right)}^2}} \;\;\;\;\;SST = total\;sum\;of\;squares SST=i=1∑m(yi−yˉ)2SST=totalsumofsquares
S S R = ∑ i = 1 m ( y ^ i − y ˉ ) 2 S S R = s u m o f d u e t o r e g r e s s i o n SSR = \sum\limits_{i = 1}^m {{{\left( {{{\hat y}_i} - \bar y} \right)}^2}} \;\;\;\;\;SSR = sum\;of\;due\;to\;regression SSR=i=1∑m(y^i−yˉ)2SSR=sumofduetoregression
S S E = ∑ i = 1 m ( y ^ i − y i ) 2 S S E = s u m o f d u e t o e r r o s SSE = \sum\limits_{i = 1}^m {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} \;\;\;\;\;SSE = sum\;of\;due\;to\;erros SSE=i=1∑m(y^i−yi)2SSE=sumofduetoerros
S S T = S S R + S S E SST = SSR + SSE SST=SSR+SSE
R 2 ( y , y ^ ) = S S R S S T {R^2}(y,\hat y) = \frac{{SSR}}{{SST}} R2(y,y^)=SSTSSR
如果结果是0,就说明模型预测不能预测因变量;如果结果是1。就说明是函数关系;如果结果是0-1之间的数,就是我们模型的好坏程度。
化简上面的公式,分子就变成了我们的均方误差MSE,下面分母就变成了方差:
R 2 ( y , y ^ ) = 1 − S S E S S T = 1 − ∑ i = 1 m ( y i − y ^ i ) 2 ∑ i = 1 m ( y i − y ˉ ) 2 = 1 − ∑ i = 1 m ( y i − y ^ i ) 2 / m ∑ i = 1 m ( y i − y ˉ ) 2 / m = 1 − M S E ( y , y ^ ) V a r ( y ) {R^2}(y,\hat y) = 1 - \frac{{SSE}}{{SST}} = 1 - \frac{{\sum\limits_{i = 1}^m {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^m {{{\left( {{y_i} - \bar y} \right)}^2}} }} = 1 - \frac{{\sum\limits_{i = 1}^m {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} /m}}{{\sum\limits_{i = 1}^m {{{\left( {{y_i} - \bar y} \right)}^2}} /m}} = 1 - \frac{{MSE(y,\hat y)}}{{Var(y)}} R2(y,y^)=1−SSTSSE=1−i=1∑m(yi−yˉ)2i=1∑m(yi−y^i)2=1−i=1∑m(yi−yˉ)2/mi=1∑m(yi−y^i)2/m=1−Var(y)MSE(y,y^)
问题 5: 以上评估指标有没有缺陷,如果有,该怎样改进?
以上的评估指标是基于误差的均值对进行评估的,均值对异常点(outliers)较敏感,如果样本中有一些异常值出现,会对以上指标的值有较大影响,即均值是非鲁棒的。
2.1.5、解决评估指标鲁棒性问题
我们通常用以下两种方法解决评估指标的鲁棒性问题:
(1)剔除异常值:设定一个相对误差,当该值超过一定的阈值时,则认为其是一个异常点,剔除这个异常点,将异常点剔除之后。再计算平均误差来对模型进行评价。
(2)使用误差的分位数来代替:如利用中位数来代替平均数。例如 MAPE:
M A P E = 100 % n ∑ i = 1 n ∣ y ^ i − y i y i ∣ MAPE = \frac{{100\% }}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|} MAPE=n100%i=1∑n∣∣∣∣yiy^i−yi∣∣∣∣
MAPE是一个相对误差的中位数,当然也可以使用别的分位数。
2.2、分类(Classification)算法指标
- Accuracy 精度
- Confusion Matrix 混淆矩阵
- Precision 准确率(查准率)
- Recall 召回率(查全率)
- Fβ Score
- AUC Area Under Curve
- KS Kolmogorov-Smirnov
2.2.1、精度 ACC
预测正确的样本的占总样本的比例,取值范围为[0,1],取值越大,模型预测能力越好。
A c c ( y , y ^ ) = 1 m ∑ i = 1 m s i g n ( y ^ i , y i ) Acc(y,\hat y) = \frac{1}{m}\sum\limits_{i = 1}^m {sign\left( {{{\hat y}_i},{y_i}} \right)} Acc(y,y^)=m1i=1∑msign(y^i,yi)
精度评价指标ACC平等对待每个类别,即每一个样本判对 (0) 和判错 (1) 的代价都是一样的。
问题 6: 精度ACC有什么缺陷?什么时候精度指标会失效?
(1)对于有倾向性的问题,往往不能用精度指标来衡量。
比如,判断空中的飞行物是导弹还是其他飞行物,很显然为了减少损失,我们更倾向于相信是导弹而采用相应的防护措施。此时判断为导弹实际上是其他飞行物与判断为其他飞行物实际上是导弹这两种情况的重要性是不一样的;
(2)对于样本类别数量严重不均衡的情况,也不能用精度指标来衡量。
比如银行客户样本中好客户990个,坏客户10个。如果一个模型直接把所有客户都判断为好客户,得到精度为99%,但这显然是没有意义的。
对于以上两种情况,单纯根据Accuracy来衡量算法的优劣已经失效。这个时候就需要对目标变量的真实值和预测值做更深入的分析。
2.2.2、混淆矩阵Confusion Matrix
对于最常见的二元分类来说,它的混淆矩阵是2*2的,如下:
| 预测值 正 | 预测值 负 | |
|---|---|---|
| 真实值 正 | TP | FN |
| 真实值 负 | FP | TN |
这里牵扯到三个方面:真实值,预测值,预测值和真实值之间的关系,其中任意两个方面都可以确定第三个。通常取预测值和真实值之间的关系、预测值对矩阵进行划分:
(1)True positive (TP) —真阳性
真实值为Positive,预测正确(预测值为Positive)
(2)True negative (TN)—真阴性
真实值为Negative,预测正确(预测值为Negative)
(3)False positive (FP) —假阳性
真实值为Negative,预测错误(预测值为Positive),第一类错误, Type I error。
(4)False negative (FN) —假阴性
真实值为Positive,预测错误(预测值为 Negative),第二类错误, Type II error。
比如我们一个模型对15个样本进行预测,然后结果如下。
真实值:0 1 1 0 1 1 0 0 1 0 1 0 1 0 0
预测值:1 1 1 1 1 0 0 0 0 0 1 1 1 0 1
则混淆矩阵为:
| 预测值=1 | 预测值=0 | 预测值=1 | 预测值=0 | ||
|---|---|---|---|---|---|
| 真实值=1 | 5 | 2 | 真实值=1 | TP | FN |
| 真实值=0 | 4 | 4 | 真实值=0 | FP | TN |
2.2.3、准确率(查准率) Precision
Precision 是分类器预测的正样本中预测正确的比例,取值范围为[0,1],取值越大,模型预测能力越好。
P = T P T P + F P P = \frac{{TP}}{{TP + FP}} P=TP+FPTP
2.2.4、召回率(查全率)Recall
Recall 是分类器所预测正确的正样本占所有正样本的比例,取值范围为[0,1],取值越大,模型预测能力越好。
R = T P T P + F N R = \frac{{TP}}{{TP + FN}} R=TP+FNTP
应用场景:
(1)地震的预测
对于地震的预测,我们希望的是Recall非常高,也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲Precision。情愿发出1000次警报,把10次地震都预测正确了;也不要预测100次对了8次漏了两次。
即可以多点虚警,但少点漏检。“宁错拿一万,不放过一个”,分类阈值较低
(2)嫌疑人定罪
基于不错怪一个好人的原则,对于嫌疑人的定罪我们希望是非常准确的。即使有时候放过了一些罪犯,但也是值得的。因此我们希望有较高的Precision值,可以合理地牺牲Recall。
即可以多点漏检,但少点虚警。“宁放过一万,不错拿一个”,“疑罪从无”,分类阈值较高。
问题 7: 某一家互联网金融公司风控部门的主要工作是利用机器模型抓取坏客户。互联网金融公司要扩大业务量,尽量多的吸引好客户,此时风控部门该怎样调整Recall和Precision?如果公司坏账扩大,公司缩紧业务,尽可能抓住更多的坏客户,此时风控部门该怎样调整Recall和Precision?
如果互联网公司要扩大业务量,为了减少好客户的误抓率,保证吸引更多的好客户,风控部门就会提高阈值,从而提高模型的查准率Precision,同时,导致查全率Recall下降。如果公司要缩紧业务,尽可能抓住更多的坏客户,风控部门就会降低阈值,从而提高模型的查全率Recall,但是这样会导致一部分好客户误抓,从而降低模型的查准率 Precision。
根据以上个案,我们知道随着阈值的变化Recall和Precision往往会向着反方向变化,这种规律很难满足我们的期望,即Recall和Precision同时增大。
问题 8: 有没有什么方法权衡Recall和Precision 的矛盾?
我们可以用一个指标来统一Recall和Precision的矛盾,即利用Recall和Precision的加权调和平均值作为衡量标准。
2.2.5、Fβ Score
Precision和Recall 是互相影响的,理想情况下肯定是希望做到两者都高,但是一般情况下Precision高、Recall 就低, Recall 高、Precision就低。为了均衡两个指标,我们可以采用Precision和Recall的加权调和平均(weighted harmonic mean)来衡量,即Fβ Score,公式如下:
F β = ( 1 + β 2 ) × P × R β 2 × P + R {F_\beta } = (1 + {\beta ^2}) \times \frac{{P \times R}}{{{\beta ^2} \times P + R}} Fβ=(1+β2)×β2×P+RP×R
β表示权重;
F β = ( 1 + β 2 ) × P × R β 2 × P + R = 1 β 2 ( 1 + β 2 ) × R + 1 ( 1 + β 2 ) × P = 1 1 ( 1 + 1 β 2 ) × R + 1 ( 1 + β 2 ) × P \begin{gathered} {F_\beta } = \frac{{(1 + {\beta ^2}) \times P \times R}}{{{\beta ^2} \times P + R}} \\ = \frac{1}{{\frac{{{\beta ^2}}}{{(1 + {\beta ^2}) \times R}} + \frac{1}{{(1 + {\beta ^2}) \times P}}}} \\ = \frac{1}{{\frac{1}{{(1 + \frac{1}{{{\beta ^2}}}) \times R}} + \frac{1}{{(1 + {\beta ^2}) \times P}}}} \\ \end{gathered} Fβ=β2×P+R(1+β2)×P×R=(1+β2)×Rβ2+(1+β2)×P11=(1+β21)×R1+(1+β2)×P11
通俗的就是:β越大,Recall的权重越大,β越小,Precision的权重越大。
由于Fβ Score 无法直观反映数据的情况,同时业务含义相对较弱,实际工作用到的不多。
2.2.6、ROC 和 AUC
AUC是一种模型分类指标,且仅仅是二分类模型的评价指标。AUC是Area Under Curve的简称,那么Curve就是 ROC(Receiver Operating Characteristic),翻译为"接受者操作特性曲线"。也就是说ROC是一条曲线,AUC是一个面积值。
(1)ROC
ROC曲线为 FPR 与 TPR 之间的关系曲线,这个组合以 FPR 对 TPR,即是以代价 (costs) 对收益 (benefits),显然收益越高,代价越低,模型的性能就越好。
- x轴为假阳性率(FPR):在所有的负样本中,分类器预测错误的比例—代价
F P R = F P F P + T N FPR = \frac{{FP}}{{FP + TN}} FPR=FP+TNFP - y轴为真阳性率(TPR):在所有的正样本中,分类器预测正确的比例(等于Recall)—收益
T P R = T P T P + F N TPR = \frac{{TP}}{{TP + FN}} TPR=TP+FNTP
为了更好地理解ROC曲线,我们使用具体的实例来说明:
如在医学诊断的主要任务是尽量把生病的人群都找出来,也就是TPR越高越好。而尽量降低没病误诊为有病的人数,也就是FPR越低越好。
不难发现,这两个指标之间是相互制约的。**如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的TPR应该会很高,但是FPR也就相应地变高。**最极端的情况下,他把所有的样本都看作有病,那么TPR达到1,FPR也为1。
我们以FPR为横轴,TPR为纵轴,得到如下ROC空间:

我们可以看出,
- 左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对;
- 点A(TPR>FPR),医生A的判断大体是正确的;
- 中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;
- 下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医;
上图中一个阈值,得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何,也就是遍历所有的阈值,得到 ROC 曲线。示意图如下所示:

假设上图是某医生的诊断统计图,为未得病人群(上部分)和得病人群(下部分)的模型输出概率分布图(横坐标表示模型输出概率,纵坐标表示概率对应的人群的数量),显然未得病人群的概率值普遍低于得病人群的输出概率值(即正常人诊断出疾病的概率小于得病人群诊断出疾病的概率)。
竖线代表阈值。显然,图中给出了某个阈值对应的混淆矩阵,通过改变不同的阈值 ,得到一系列的混淆矩阵,进而得到一系列的TPR和FPR,绘制出ROC曲线。
阈值为1时,不管你什么症状,医生均未诊断出疾病(预测值都为N),此时,位于左下。阈值为 0 时,不管你什么症状,医生都诊断结果都是得病(预测值都为P),此时,位于右上。
(2)AUC
AUC定义:
- AUC 值为 ROC 曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
- AUC = 1,是完美分类器,代价为0,收益为最高。
- 0.5 < AUC < 1,优于随机猜测。有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
注:对于AUC小于 0.5 的模型,我们可以考虑取反(模型预测为positive,那我们就取negtive),这样就可以保证模型的性能不可能比随机猜测差。
以下为ROC曲线和AUC值的实例:

AUC的物理意义 :AUC的物理意义是正样本的预测结果大于负样本的预测结果的概率。所以AUC反映的是分类器对样本的排序能力。另外值得注意的是,AUC对样本类别是否均衡并不敏感,这也是不均衡样本通常用AUC评价分类器性能的一个原因。
问题 13 :小明一家四口,小明5岁,姐姐10岁,爸爸35岁,妈妈33岁,建立一个逻辑回归分类器,来预测小明家人为成年人概率。
以下为三种模型的输出结果,求三种模型的 AUC :
| 小明 | 姐姐 | 妈妈 | 爸爸 | |
|---|---|---|---|---|
| a | 0.12 | 0.35 | 0.76 | 0.85 |
| b | 0.12 | 0.35 | 0.44 | 0.49 |
| c | 0.52 | 0.65 | 0.76 | 0.85 |
- AUC更多的是关注对计算概率的排序,**关注的是概率值的相对大小,与阈值和概率值的绝对大小没有关系。**例子中并不关注小明是不是成人,而关注的是,预测为成人的概率的排序。
- AUC只关注正负样本之间的排序,并不关心正样本内部,或者负样本内部的排序。这也体现了AUC的本质: 任意个正样本的概率都大于负样本的概率的能力。
以例子进行说明解释,其中AUC只需要保证负样本(小明和姐姐),正样本(爸爸和妈妈),小明和姐姐在前2个排序,爸爸和妈妈在后2个排序,而不会考虑小明和姐姐谁在前,或者爸爸和妈妈谁在前。
AUC只与概率的相对大小(概率排序)有关,和绝对大小没关系。由于三个模型概率排序的前两位都是未成年人(小明,姐姐),后两位都是成年人(妈妈,爸爸),因此三个模型的AUC都等于1。
问题 14:以下已经对分类器输出概率从小到大进行了排列,哪些情况的AUC等于1, 情况的AUC为0(其中背景色表示True value,红色表示成年人,蓝色表示未成年人)。

D 模型, E模型和F模型的AUC值为1,C 模型的AUC值为0(爸妈为成年人的概率小于小明和姐姐,显然这个模型预测反了)。
AUC的计算:
法1:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积(曲线)之和。计算的精度与阈值的精度有关。
法2:根据AUC的物理意义,我们计算正样本预测结果大于负样本预测结果的概率。取n1* n0(n1为正样本数,n0为负样本数)个二元组,每个二元组比较正样本和负样本的预测结果,正样本预测结果高于负样本预测结果则为预测正确,预测正确的二元组占总二元组的比率就是最后得到的AUC。时间复杂度为O(N* M)。
法3:我们首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n (n=n0+n1,其中n0为负样本个数,n1为正样本个数),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有n1-1个其他正样本比他score小,那么就有(rank_max-1)-(n1-1)个负样本比他score小。其次为(rank_second-1)-(n1-2)。最后我们得到正样本大于负样本的概率为 :
A U C = ∑ r a n k ( s c o r e ) − n 1 ∗ ( n 1 + 1 ) 2 n 0 ∗ n 1 AUC = \frac{{\sum\nolimits_{} {rank(score)} - \frac{{{n_1} * ({n_1} + 1)}}{2}}}{{{n_0} * {n_1}}} AUC=n0∗n1∑rank(score)−2n1∗(n1+1)
其计算复杂度为O(N+M)。
下面有一个简单的例子:
真实标签为 (1, 0, 0, 1, 0) ,预测结果1(0.9, 0.3, 0.2, 0.7, 0.5) ,预测结果2(0.9, 0.3, 0.2, 0.7, 0.8)。分别对两个预测结果进行排序(从小到大),并提取他们的序号。结果1 (5, 2, 1, 4, 3) ,结果2 (5, 2, 1, 3, 4)
对正分类序号累加,结果1:SUM正样本(rank(score))=5+4=9, 结果2: SUM正样本(rank(score))=5+3=8
计算两个结果的AUC:
结果1:AUC= (9-2 * 3/2)/6=1
结果2:AUC= (8-2 * 3/2)/6=0.833。
问题 15:为什么说 ROC 和AUC都能应用于非均衡的分类问题?
ROC曲线只与横坐标 (FPR) 和 纵坐标 (TPR) 有关系。**我们可以发现TPR只是正样本中预测正确的概率,而FPR只是负样本中预测错误的概率,和正负样本的比例没有关系。**因此 ROC 的值与实际的正负样本比例无关,因此既可以用于均衡问题,也可以用于非均衡问题。
而 AUC 的几何意义为ROC曲线下的面积,因此也和实际的正负样本比例无关。
2.2.7、KS Kolmogorov-Smirnov
KS值是在模型中用于区分预测正负样本分隔程度的评价指标,一般应用于金融风控领域。
与ROC曲线相似,ROC是以FPR作为横坐标,TPR作为纵坐标,通过改变不同阈值,从而得到ROC曲线。而在KS曲线中,则是以阈值作为横坐标,以FPR和TPR作为纵坐标,ks曲线则为TPR减FPR,ks曲线的最大值通常为ks值。
为什么这样求KS值呢?我们知道,当阈值减小时,TPR和FPR会同时减小,当阈值增大时,TPR和FPR会同时增大。而在实际工程中,我们希望TPR更大一些,FPR更小一些,即TPR-FPR越大越好,即ks值越大越好。
可以理解TPR是收益,FPR是代价,ks值是收益最大。图中绿色线是TPR、蓝色线是FPR,红色线是KS线,ks曲线的最大值通常为ks值。

3、深度学习目标检测评估性能指标
3.1、一个例子—Precision和Recall
以下图Big three人脸检测为例,图中有3个红框标示的人脸,即常说的Ground truth。

那么检测结果分为以下几种情况:对于真实的人脸,即正样本,也就是红框区域:True positive(TP):正确的正样本,即检测器找到出了人脸;False negative(FN):错误的负样本,即检测器把人脸区域当作非人脸拒绝了,也叫做漏检;True negative(TN):检测器把背景判定成了背景,没问题;False positive(FP):检测器把不是人脸的目标当作人脸,也叫虚警。
- TP:实际情况是人脸,检测结果为人脸,正确的检测结果
- TN:实际情况是背景,检测结果为背景,正确的检测结果
- FP:实际情况是背景,检测结果为人脸,也就是误检
- FN:实际情况是人脸,检测结果为背景,也就是漏检
假设绿色实线的框代表检测器输出结果,绿色虚线框代表检测器漏掉了(即应该有输出但是却没有),看图:

其实FN/FP都是错误情况,检测器出错了,但是这2种错误好像还不太一样。那么我们算2个指标:
(1)准确率Precision
所谓Precision就是所有输出检测框的正确度:(在物体检测里面,总的检测结果其实就是最后输出的框的总数)
Pr e c i s i o n = T P T P + F P = 2 4 \Pr ecision = \frac{{TP}}{{TP + FP}} = \frac{2}{4} Precision=TP+FPTP=42
(2)召回率Recall
所谓Recall就是所有检测出框的召回率,即检测器找到了多少个真的人脸目标:
Re c a l l = T P T P + F N = 2 3 \operatorname{Re} call = \frac{{TP}}{{TP + FN}} = \frac{2}{3} Recall=TP+FNTP=32
在实际情况中,Precision/Recall往往是一对冤家。如果上面的人脸检测器输出了1个框,那么Precsion=1/(1+0)=100%,Recall=1/(1+2)=33.3%;又如果上面的人脸检测器输出了100个框,那么Precsion=3/(100)=3%,Recal=3/(3+0)=100%。看吧,就像一个跷跷板。
考虑应用场景:
场景1:汽车辅助驾驶系统,如果汽车前方有行人,紧急情况下系统帮助驾驶员提前刹车。那么这时候要求Precision一定要高。由于辅助系统会帮助驾驶员刹车,那么就要求检测器输出的行人一定是真的行人。否则系统一直检测出非行人的奇怪东西(如电线杆),导致汽车不停的刹车,驾驶员不砸了车才怪。
场景2:某银行安防系统电子眼背后的检测器,检测到可疑人就报警。这时候要求Recall要高。安防么,杀错一千也不能漏掉一个,漏掉就意味着出很大的问题。你应该理解。
所以,综合考虑Precision/Recall跷跷板和应用场景,怎么可能有统一的标准!
3.2、如何评判检测器的好坏?
对于一般目标检测算法,对于每个框输出如下:
x,y,width,height,confidence
其中检测框Rectange [x,y,width,height]代表检测框在当前图中的位置,而conifidence代表当前框是目标的置信度,一般情况0<conifidence<1。
在实际评测的时候,会进行后处理,只有confience>thresh_conf的时候才输出,否则直接过滤掉。而输出的框必须符合检测框Rectangle与GT之间的IoU必须大于某个阈值thresh_iou才会被判断为TP:

多说一句,在实际情况中,检测器会输出:高的confidence的大+清晰的目标,低的confidence的远+模糊的目标,同时还有极低confidence的错误检测。

了解这些基本问题后,来看指标。
3.3、常用性能指标
3.3.1、PR曲线
PR = Precision vs Recall,则PR曲线如下所示:

调整thresh_conf,计算不同thresh_conf下检测器的Precision和Recall值,然后连接成曲线,就是PR曲线了。
具体来看:
thresh_conf很大时,检测器绝大部分框都被后处理过滤了,这时候输出的框都是置信度很大的框。如图2设置阈值为0.8,那么除了confidence最高的另外5个检测框都被过滤了。这时Precision很高,Recall很低
thresh_conf很小时,检测器输出了很多框,各种妖魔鬼怪都被放出来了。如图2设置阈值为0.05,所有的框都输出了。这时Precision很低,Recall很高。
看到这应该理解了隐藏在PR曲线中,没画出来的另外一个thresh_conf维度。如下图所示:

显然PR曲线越往右上角,检测器的性能越好。
3.3.2、mAP
mAP = mean average precision
你以为有PR曲线就万事大吉了?现实中的PR曲线往往是这样:

所以无法正常的判断哪条曲线好。所以来看看PR曲线的AUC(Area Under Curve),也就是PR曲线下面的面积。
从积分的角度看,PR曲线下的面积就是检测器在各个thresh_conf情况下的AP(Average Precsion)。显然,AP越高的检测器越好。
上述我们讨论的都是单类别的检测器,如只能检测出人脸,num_class=1。对于多类别CNN检测器,num_class>1,这时我们考虑计算mAP (mean Average Precsion)。
m A P = A P n u m _ c l a s s mAP = \frac{{AP}}{{num\_class}} mAP=num_classAP
依然是越大越好。
当比较mAP值,记住以下要点:
(1)mAP通常是在一个数据集上计算得到的。
(2)虽然解释模型输出的绝对量化并不容易,但mAP作为一个相对较好的度量指标可以帮助我们。当我们在流行的公共数据集上计算这个度量时,该度量可以很容易地用来比较目标检测问题的新旧方法。
(3)根据训练数据中各个类的分布情况,mAP值可能在某些类(具有良好的训练数据)非常高,而其他类(具有较少/不良数据)却比较低。所以你的mAP可能是中等的,但是你的模型可能对某些类非常好,对某些类非常不好。因此,建议在分析模型结果时查看各个类的AP值。这些值也许暗示你需要添加更多的训练样本。
3.3.3、fppi/fppw
fppi = false positive per image
如果我不关心什么mAP,更不关心你的曲线,我就想知道你这个算法平均每张图错几个。这时候就要拿出fppi曲线了:

fppi曲线的纵轴为FN/(FN+TP)(即Miss rate),横轴为false positive per image。显然相比PR曲线,fppi更接近于实际应用。至于画法,与PR曲线类似,都是通过调整thresh_conf计算相关指标画点,然后连线得到。
对应的还有fppw(fppw = false positive per window),用的少就不说了。
3.4、其余指标
除了性能之外还有速度指标与内存指标:
3.4.1、速度指标
有一些应用实时性要求非常高,比如自动驾驶,要求检测器处理每张图速度非常快。对于这些场景,速度大于一切,不能实时的检测器都是废物。
一般来说ResNet+Faster RCNN在NVIDIA GPU上可以做到1秒/图,而MobileNet+SSD在ARM芯片上可以做到300毫秒/图。这时候就应该放弃唯mAP论。
显然不能由于MobileNet+SSD的mAP比ResNet+Faster RCNN低,得出结论就是MobileNet+SSD一无是处。
3.4.2、内存指标
除了速度要求,很多应用场景对模型大小也有严格要求。比如某APP中有CNN人脸检测+识别模型,对大小有严格要求。总不能某次客户端更新,换个模型,然后告诉用户本次更新大约1GB吧。
4、结尾
这篇文章是两篇比较好的文章的汇总,如果觉得不错,请在原作者那里点赞,也在我这点赞!!,感谢!
参考文章链接:
[1] 机器学习评估指标.
[2] 白裳.