目录

前言

一、内联函数

二、typeid

三、范围for的使用

四、nullptr

五、类

六、class和访问限定符

总结

---

前言

多多重复，百炼成钢！！！

---

一、内联函数

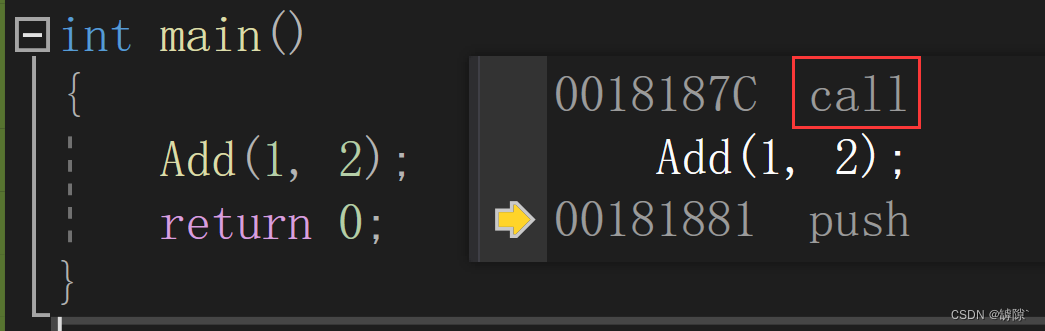
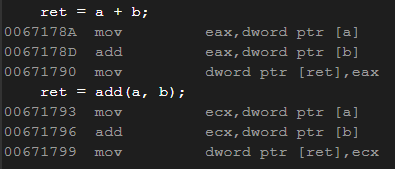
用inline修饰的函数叫内联函数-在编译时C++编译器会在函数的位置展开，没有函数调用的栈帧开销，内敛函数提升程序运行的效率。

使用场景：被频繁调用的小函数（如：swap交换函数）

1.优点：使用时在编译阶段会把函数体替换函数调用，是以一种以空间换时间的做法（在静态库/动态库）；少了调用栈帧的开销，提高了效率。

2.缺点：可能使目标文件大小变大（如安装包：后缀为.dll等）-代码膨胀

3.inline函数在编译时只是个"建议"，（一般情况下几十行以内的函数会被实现）函数规模较小，不是递归，且经常被调用的函数才被编译器采纳，否则会被忽略！（只要使用了inline修饰函数就不会进到符号表）

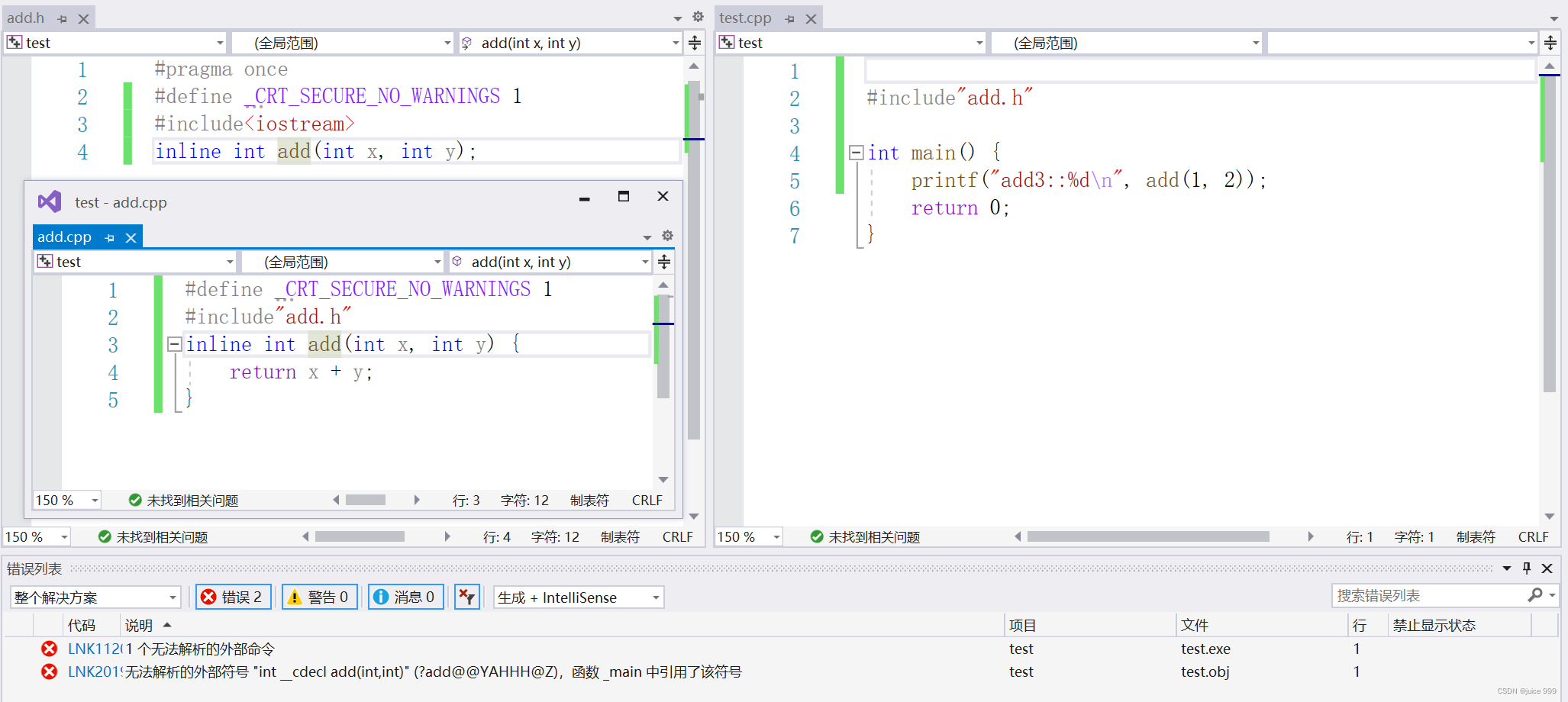
4.inline不建议声明和定义分离，分离会导致链接错误：（编译时头文件会产生相应的.o文件，编译器会到.o文件里面对照符号表找对应函数的地址为后序链接做准备，但在预处理时内联函数展开后，地址消失）inline展开后，函数地址会消失，链接找不到。（办法：直接在.h处或者.cpp处 inline定义）

没有用inline修饰： 

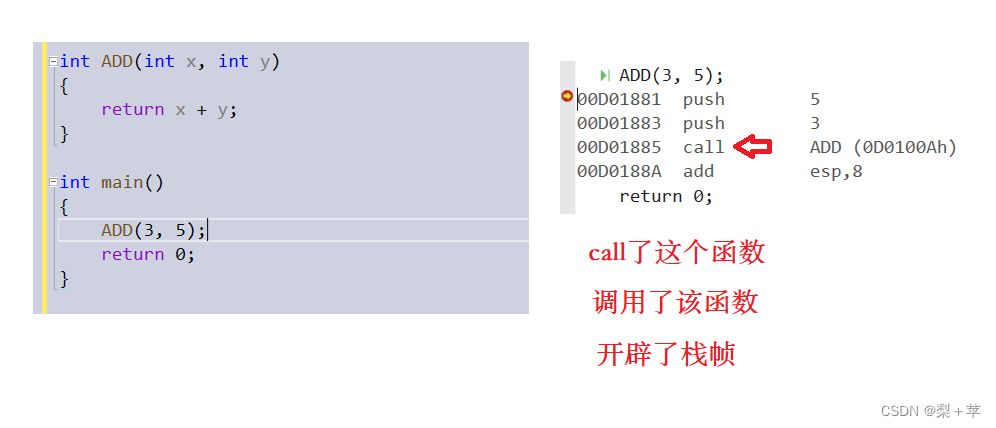
用inline修饰后：

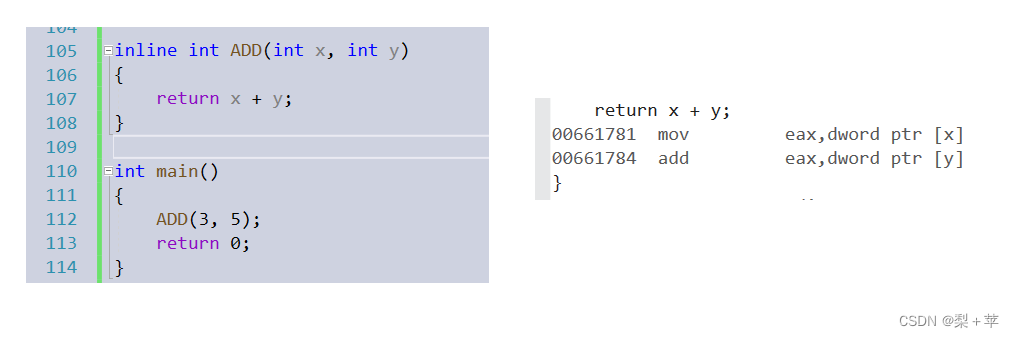
二、typeid

typeid:get到变量的类型

三、范围for的使用

e为arry的成员arry0、arry1、arry2....所以要操作时用引用 

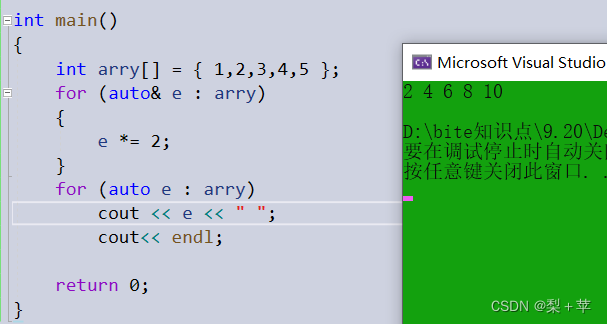
四、nullptr

1.c++中null被定义为0-bug（c语言中没有）

2.在c++中使用nullptr表示指针空值时，不需要包含头文件，它在c++11作为新关键字引入

3.在c++11中sizeof(nullptr)于sizeof((void*)0)所占字节数相同

4.建议后序表示指针空值时使用nullptr

五、类

1.c语言：struct -定义结构体 c++：struct -类（兼并了c语言中的所以用法）

2.类体中内容称为类的成员：类中的变量称为类的属性或者成员变量；类中函数称为类的方法或者成员函数。

类中两种定义方式：

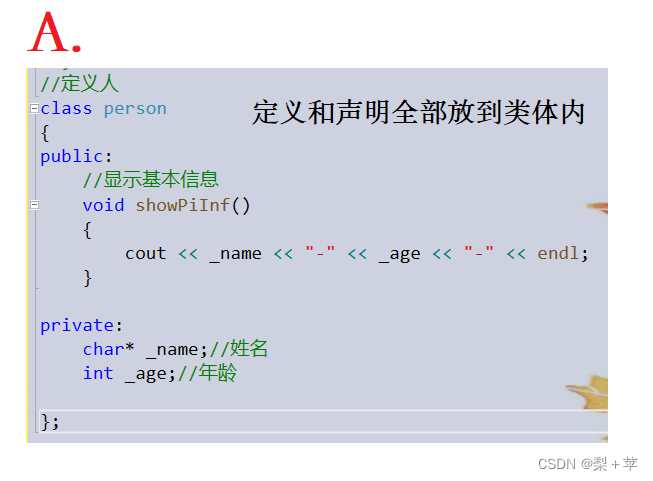
1.第一种（A）声明和定义全部放在类体中，成员函数如果在类体中定义了，则编译器可能当作内联函数处理。

2.第二种（B)类声明放在放在.h文件中，定义放在.cpp文件中，（注意：成员函数名前要放类名：：

一般情况下使用第二种！！！

 

 

 

int main()
{stack st;//类名-对象st.Init(4);st.push(34);cout << st.top() << endl;return 0;
}

六、class和访问限定符

1.class为定义类的关键字，classname为类的名字，{}中为类的主体，括号后的分号不能省略

2.类中内容称为类的成员；类中变量成为类的属性或者成员变量，类中函数称为类的函数或者成员函数

3.访问限定符：public-公有；protected-保护；private-私有

4.public修饰的成员在类外可以直接被访问，private和protected则不行

5.访问权限作用域为从该访问限定符到下一个访问限定符为止或者类的分号为止

6.class默认访问权限-private；struct默认访问权限-public（struct要兼容c）

class classname
{//成员函数...//成员变量...};

---

总结

我们需要积极的去回顾以往学过的东西噢！！！