1. 做一个4选1的mux,并且进行波形仿真 和2选1的mux对比,观察资源消耗的变化:
实验分析:4选1的mux实际上就是在2选1的mux上进行拓展,选用2位的控制信号控制4位输入信号的选择输出
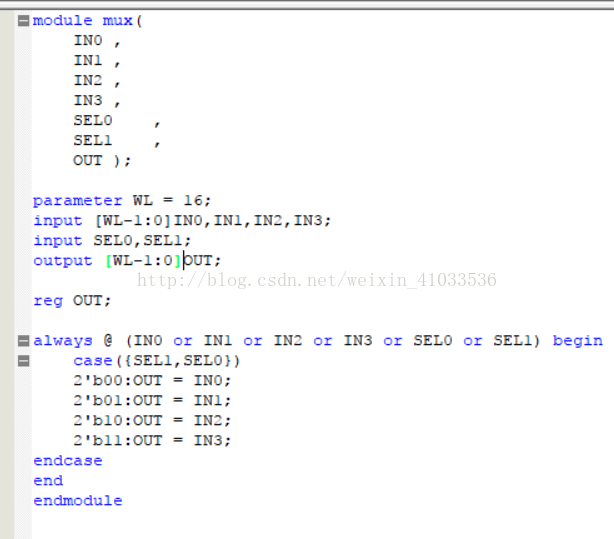
实验代码设计如下:
RTL视图如下:
波形仿真结果如下:
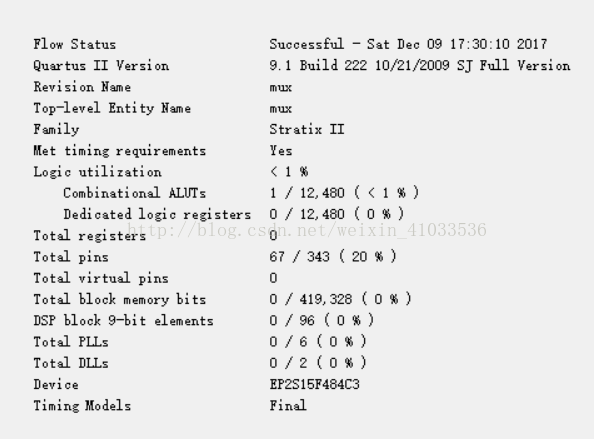
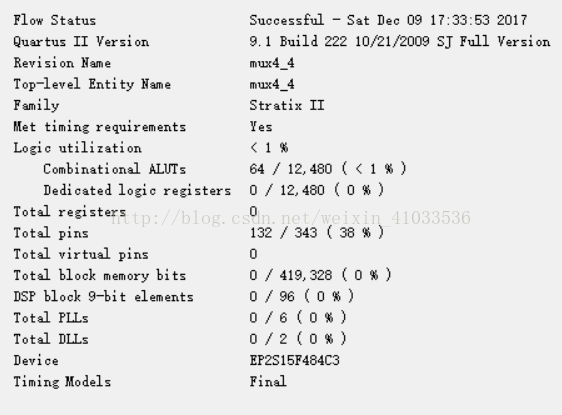
资源消耗变化如下:
4选1的mux
2选1的mux
2. 编写一个4X4路交叉开关的RTL,然后编译,看RTL View 比较2x2与4x4之间消耗资源的区别。通过对比资源,你有什么结论?
实验分析: 2X2路的交叉开关核心思想就是使用2个输出分别对应1个1位的控制信号,选择该输出哪一个输入信号。根据该思想设计4X4路的交叉开关,则每个输出对应一个2位的控制信号,从四个输入信号中选择一个进行输出,然后并联输出。
实验代码设计如下:
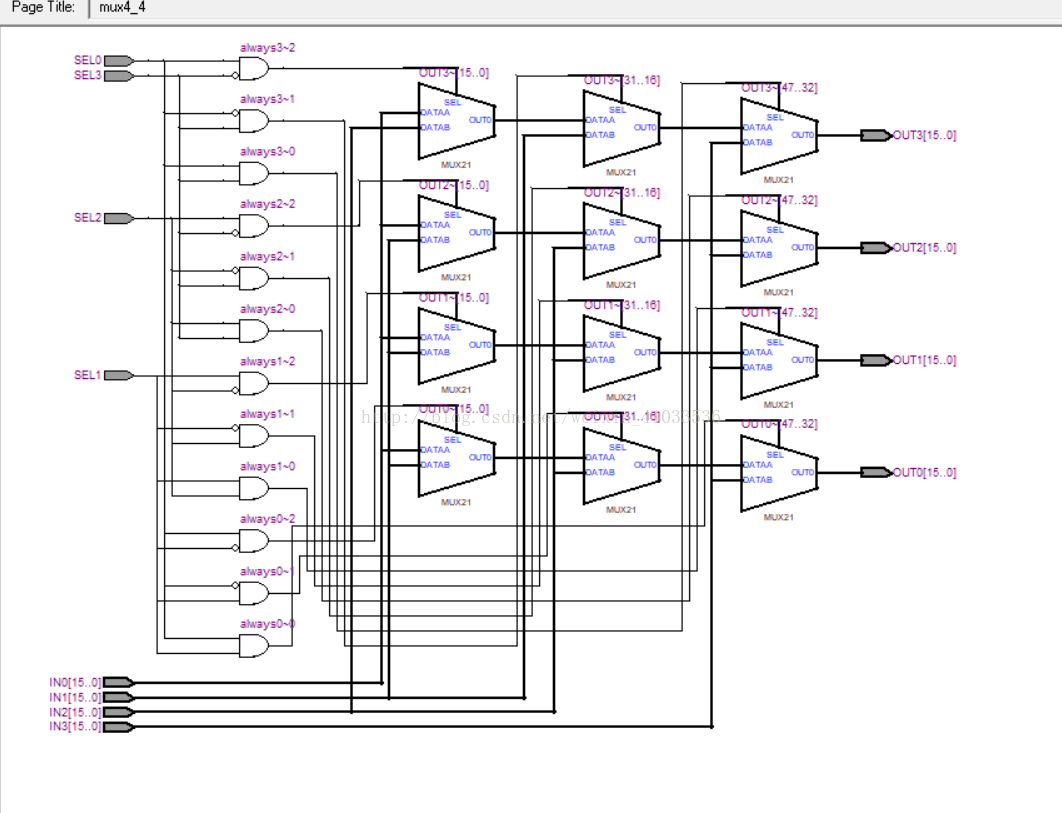
RTL视图如下:
波形仿真结果如下:
资源消耗对比如下:
4X4的交叉开关
2X2的交叉开关
可见4X4的交叉开关消耗资源成倍的增长了。
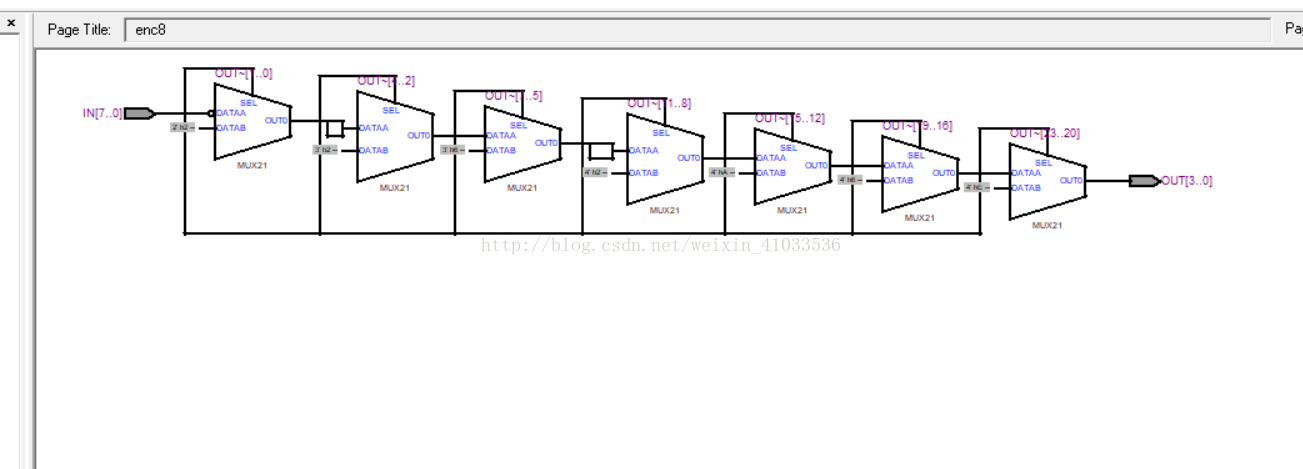
3. 编写一个8输入的优先编码器,然后编译,看RTL View:
实验分析:4输入的优先编码器本质就是一个4位输入的信号对输出进行控制,当对应为输入1时,输出与位数对应的数值,且高位输入控制优先。编写8输入的优先编码器实际上就是对4输入的位数进行一个简单拓展。
实验代码设计如下:
RTL视图如下:
波形仿真结果如下:
4. 编写一个4-16的译码器,编译;和3-8译码器对比资源开销;看RTL View:
实验分析:3-8译码器即3位输入的2进制值对应相应位置的输出位输出1。编写4-16译码器本质上是对3-8译码器输入、输出位数的一个拓展。
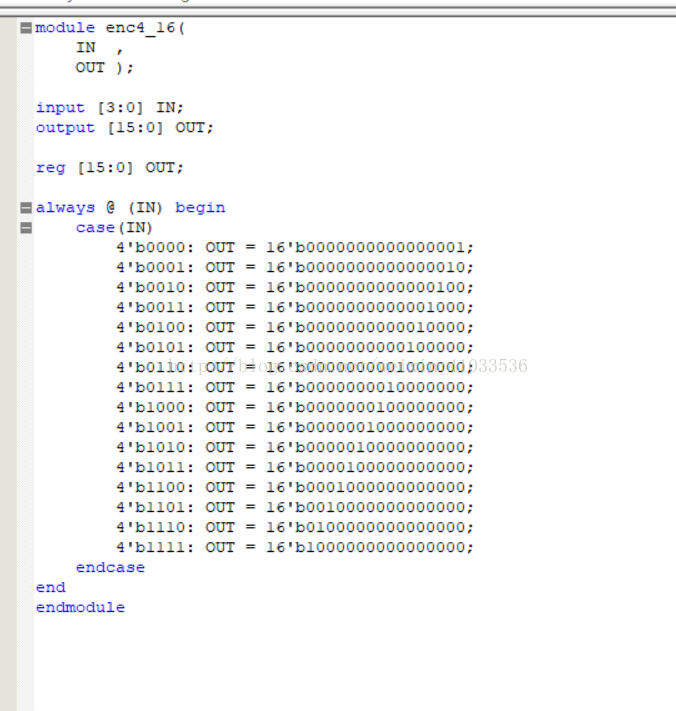
实验代码设计如下:
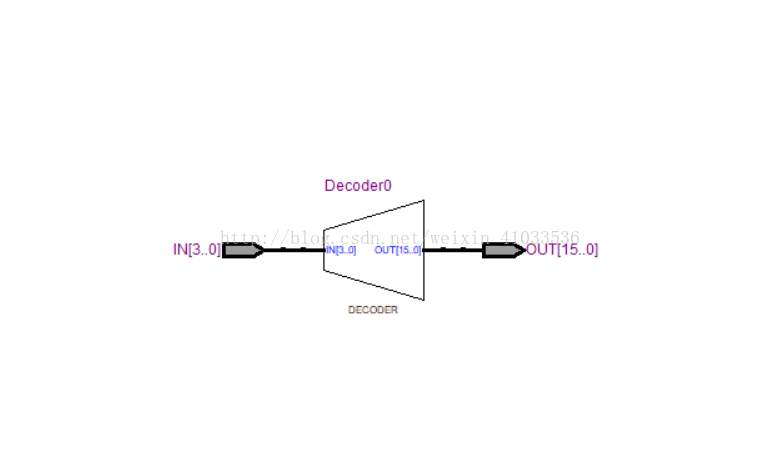
RTL视图如下:
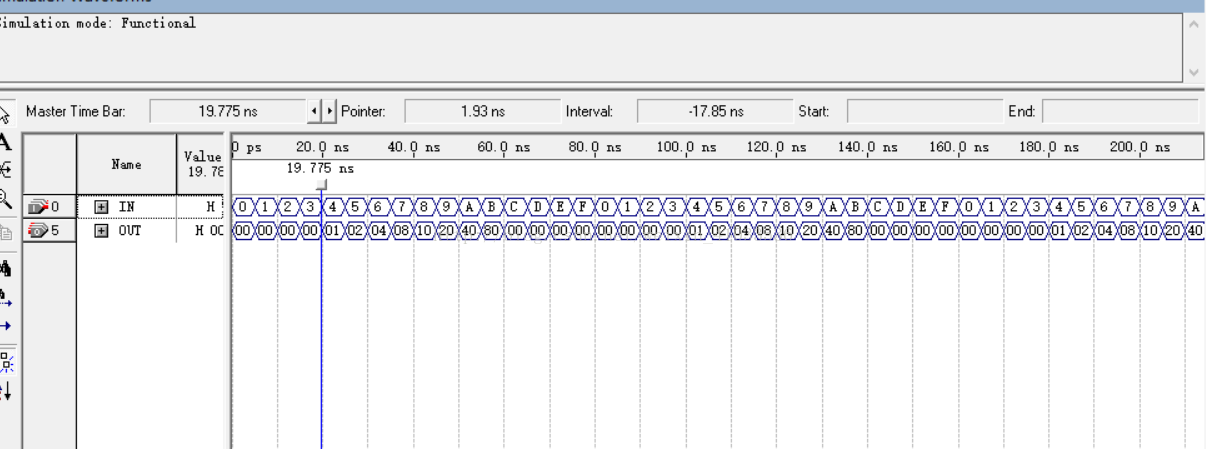
波形仿真结果如下:
资源消耗变化如下:
3-8译码器
4-16译码器
输入多了一位、输出多了八位的情况下资源消耗几乎多了一倍,可见资源消耗主要与输出位数正相关。
5. (1)把加法器的输出信号改成4比特位宽,编译,波形仿真。观察输出结果,说出输出和输入的对应关系。
(2)把加法器的输入信号改成8比特位宽,编译,波形仿真。观察加法器的输出延迟,和4比特输入位宽的情况对比,你有什么结论,为什么?
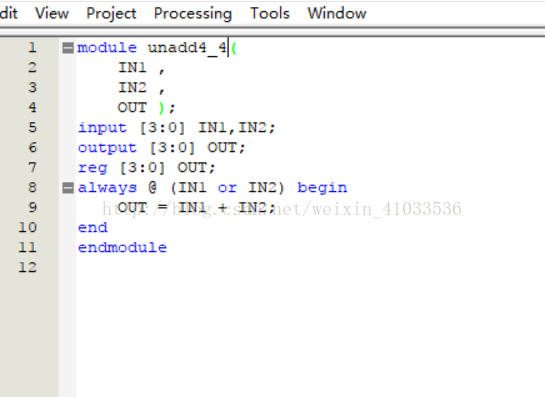
实验分析:例子程序给出无符号加法器是一个4位输入5位输出的加法器,即两个0~15的数相加,其结果范围应该在0~30。当输入仍为4位而输出改为4位时,输出结果范围仅为0~15,当两位输入相加结果大于15后输出结果会出现错误,仅能输出正确结果的后四位;而输入改为8位而输出仍为5位时,两个0~127的数相加,可结果范围只能为0~31,这时只能输出正确结果的后5位,然而加法器仍然要运算正确结果的前3位,所以输出延时应该要大于4输入-5输出的加法器。
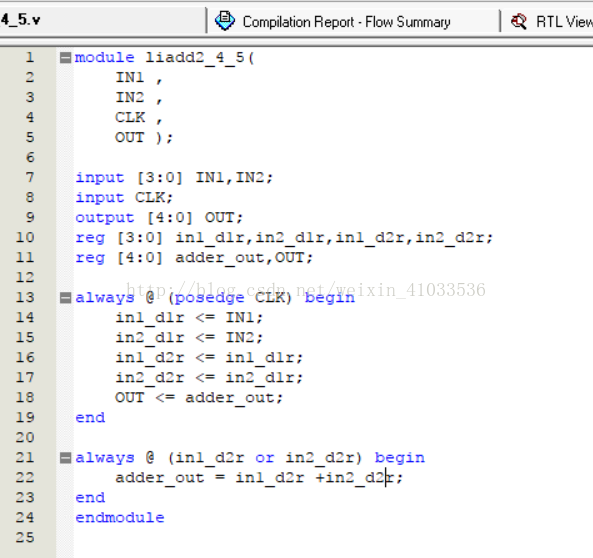
实验代码设计如下:
4输入-4输出无符号加法器
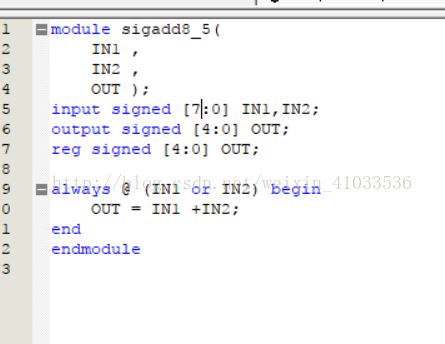
8输入-5输出无符号加法器
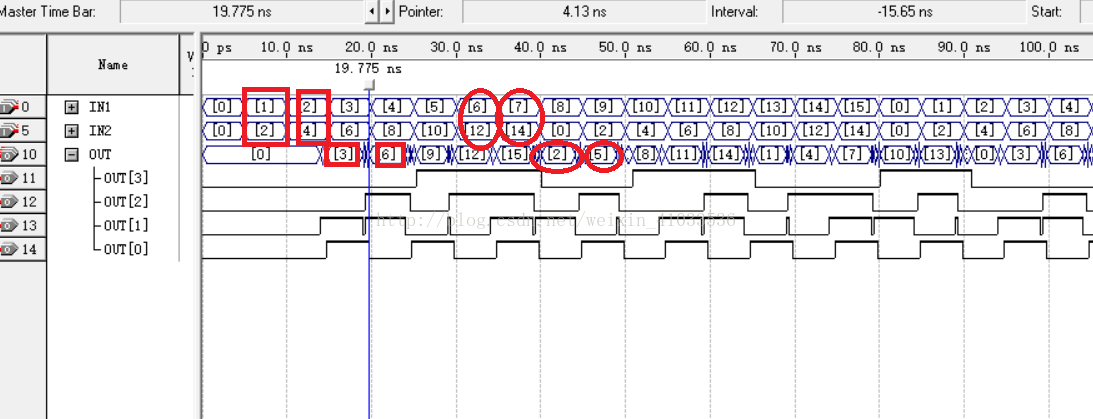
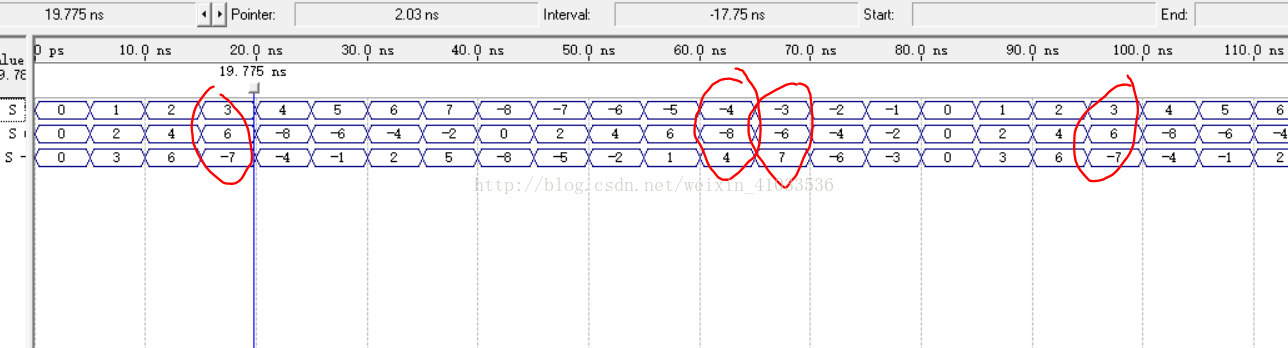
波形仿真结果如下:
4输入-4输出无符号加法器
可见当正确结果大于15后只能输出正确结果的后4位。
8输入-5输出无符号加法器
可见其输出时延稍大于4输入的无符号加法器。
6. 把加法器的输出信号改成4比特位宽,编译,波形仿真。观察输出结果,观察输出结果在什么时候是正确的?。 把加法器的输入信号改成8比特位宽,编译,波形仿真。观察加法器的输出延迟,和4比特输入位宽的情况对比,你有什么结论,为什么?
实验分析:其基本原理与上面无符号加法器相同,只不过其运算法则变为补码运算。对于组合逻辑门的层面来说,主要是“Signed”关键字生成的。
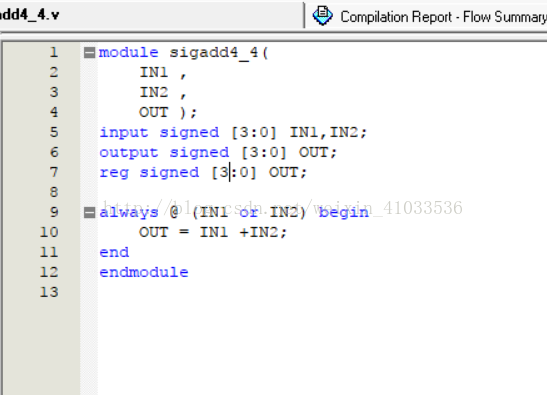
实验代码设计如下:
4输入-4输出补码加法器
8输入-5输出补码加法器
波形仿真结果如下:
4输入-4输出补码加法器
8输入-5输出补码加法器
7. 不改变流水线的级数,把加法器的输入信号改成8比特位宽,编译,波形仿真,和不带流水线的情况对比一下,你有什么结论? 在8比特输入位宽的情况下,在输入上再添加一级流水线,观察编译和仿真的结果,你有什么结论?
实验分析:与不加流水线的加法器相比,带流水线的加法器即在加法器的输入与输出都连接了D触发器,有效的减少了组合逻辑的竞争与冒险,从而明显减少了“毛刺”的长度。而流水线的级数越高,毛刺也随之越短,但输出的时延也会相应的对一个时钟周期。
实验代码设计如下:
8输入-5输出带流水线加法器
4输入-5输出2级流水线加法器
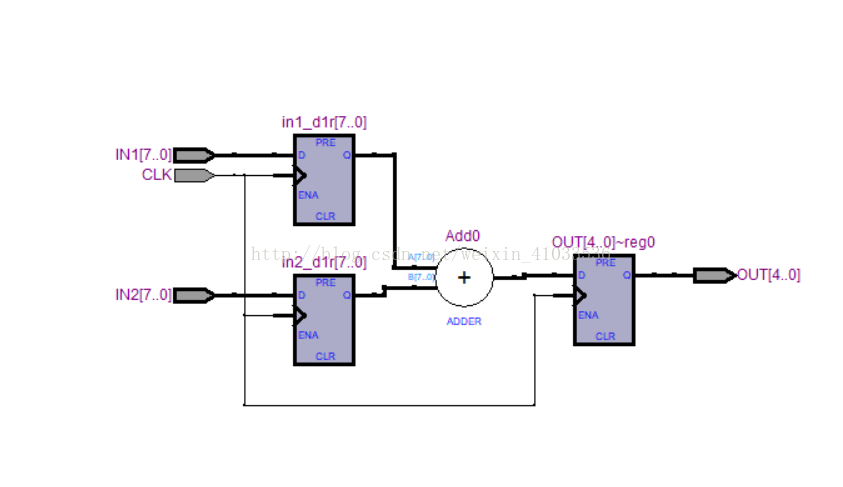
RTL视图如下:
8输入-5输出带流水线加法器
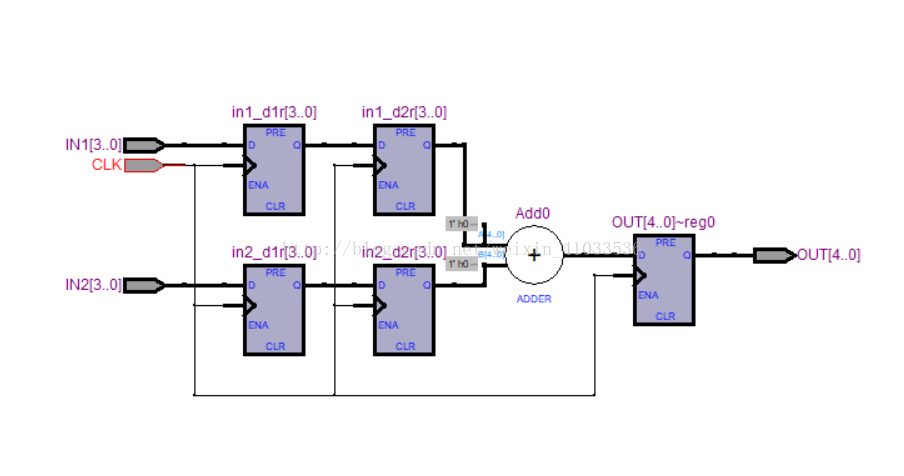
4输入-5输出2级流水线加法器
波形仿真结果如下:
8输入-5输出带流水线加法器
4输入-5输出2级流水线加法器
8. (1)改变乘法器的输入位宽为8比特,编译,波形仿真,观察信号毛刺的时间长度。
(2)选一款没有硬件乘法器的FPGA芯片(例如Cyclone EP1C6)对比8比特的乘法器和加法器两者编译之后的资源开销(Logic Cell的数目)
(3)编写一个输入和输出都有D触发器的流水线乘法器代码,编译后波形仿真,观察组合逻辑延迟和毛刺的时间,和不带流水线的情况下对比。
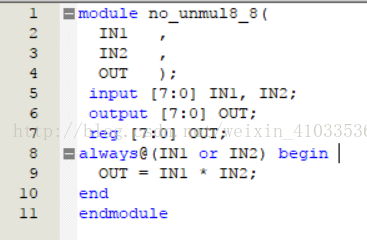
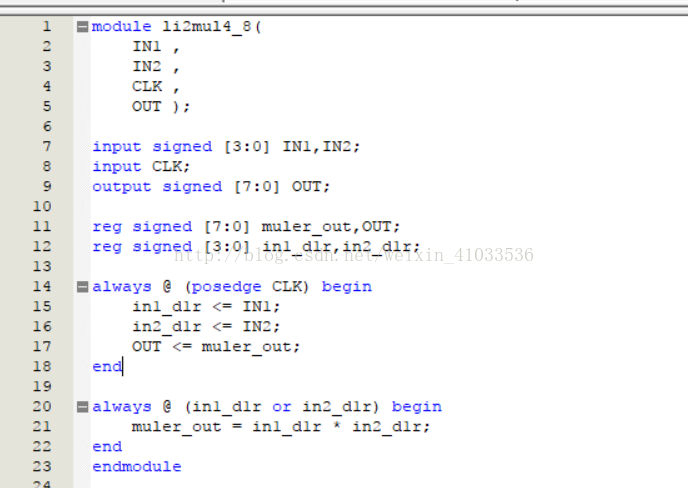
实验代码设计如下:
8输入-8输出无符号乘法器
无硬件乘法器芯片的8输入-8输出无符号乘法器
4输入-8输出带流水线乘法器
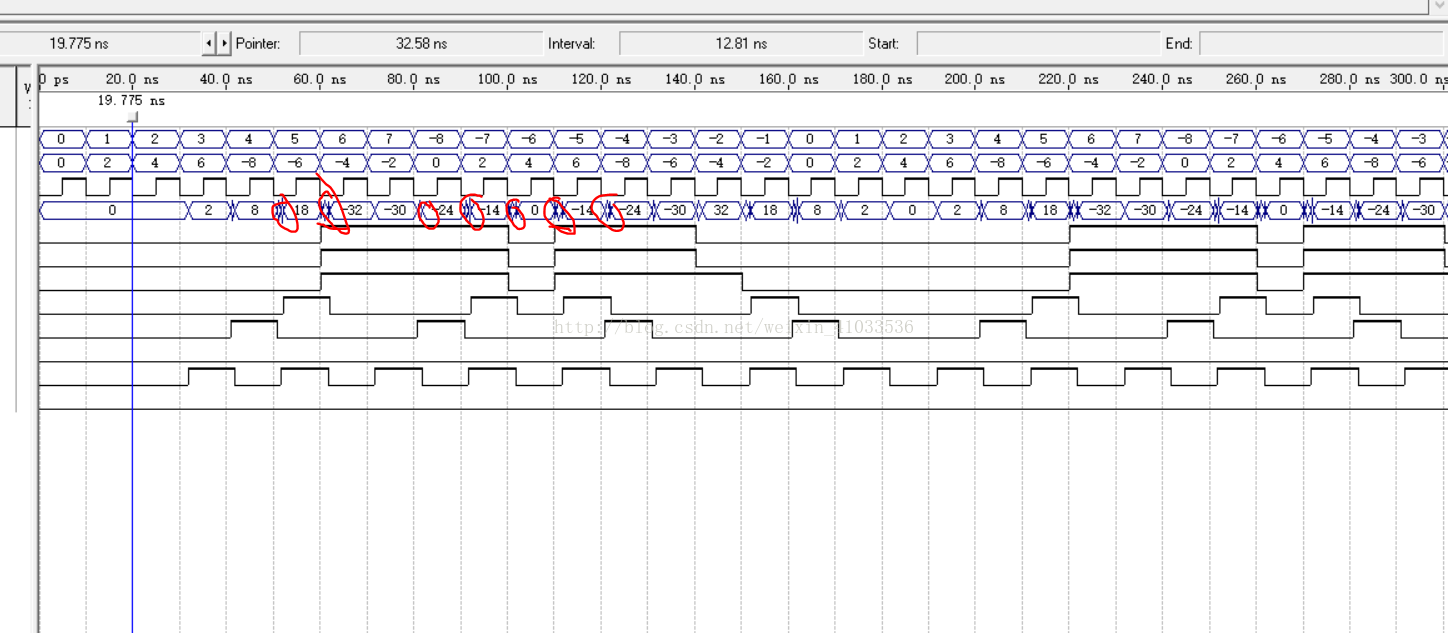
波形仿真结果如下:
8输入-8输出无符号乘法器
可见相较4输入的无符号乘法器“毛刺”时间变短。
无硬件乘法器芯片的8输入-8输出无符号乘法器
可见无硬件乘法器的无符号乘法器“毛刺”时间大大变长。
4输入-8输出带流水线乘法器
可见相较4输入-8输出无流水线乘法器,其毛刺时间相较更短,但输出延时更长(多了一个时间周期)。
资源消耗如下:
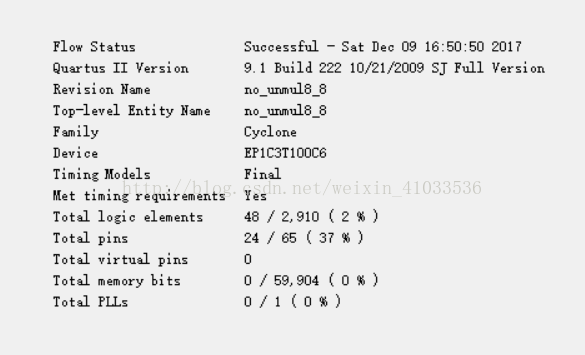
8输入-8输出无符号乘法器
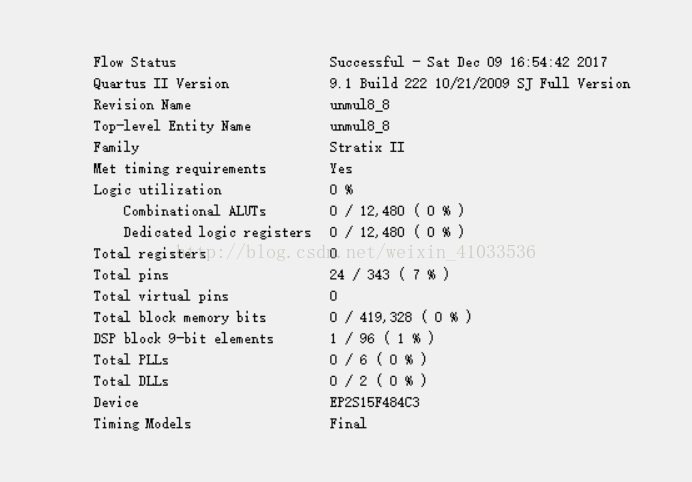
无硬件乘法器芯片的8输入-8输出无符号乘法器
可见无硬件乘法器芯片的无符号乘法器硬件资源消耗非常巨大。
9. (1)设计一个最简单的计数器,只有一个CLK输入和一个OVerflow输出,当计数到最大值的时钟周期CLK输出1
(2)设计复杂的计数器,和本例相似,带有多种信号,其中同步清零CLR的优先级最高,使能EN次之,LOAD最低。
实验分析:(1)中所要求的即不再考虑清零信号、使能信号、置数信号,当计数器还没到达最大值时,每个时间周期内计数加1,当达到计数最大值时,输出信号置1、计数置0即可;(2)即改变三个额外输入信号的优先级,只要CLR为1则执行清零,否则判断EN是否为1,为1则执行最基本的技术功能,否则执行置数功能。
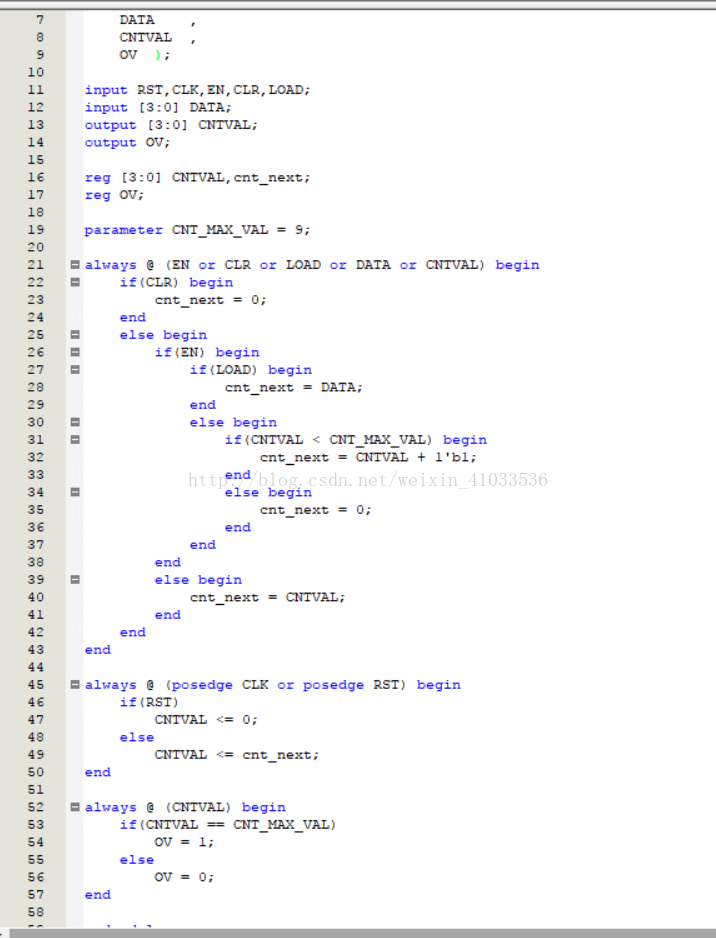
实验代码设计:
只有CLK和Overflow信号的简单计数器
改变三种信号优先级的计数器
RTL视图如下:
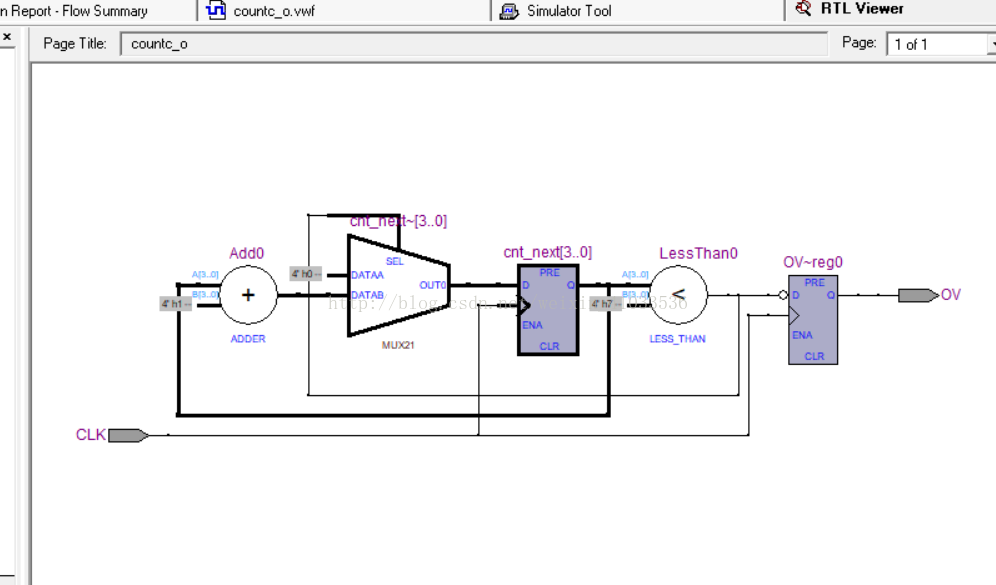
只有CLK和Overflow信号的简单计数器
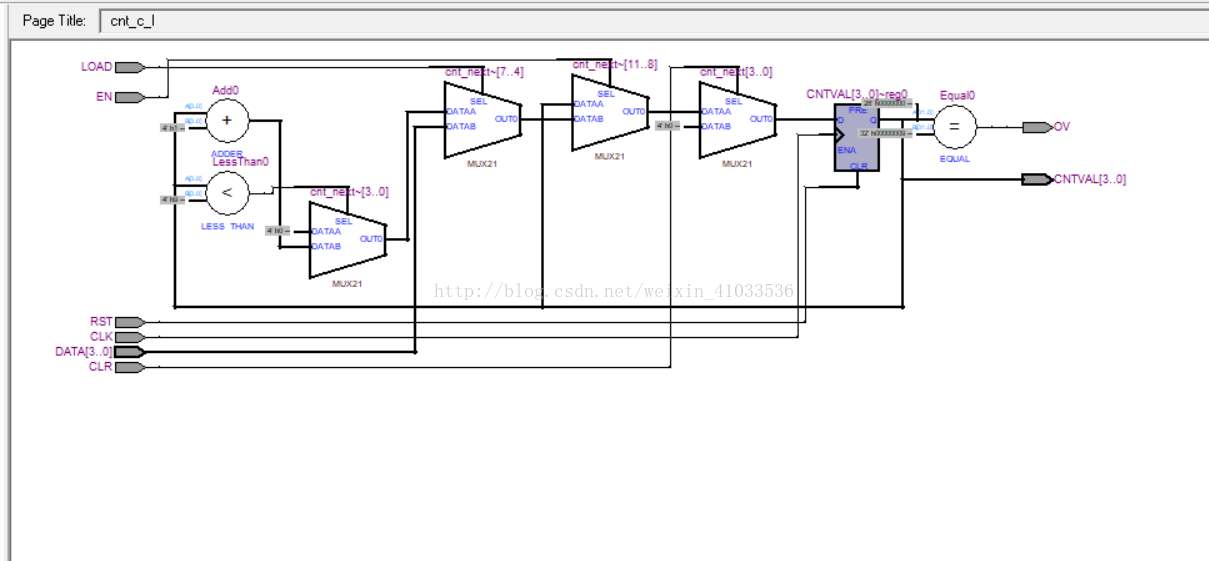
改变三种信号优先级的计数器
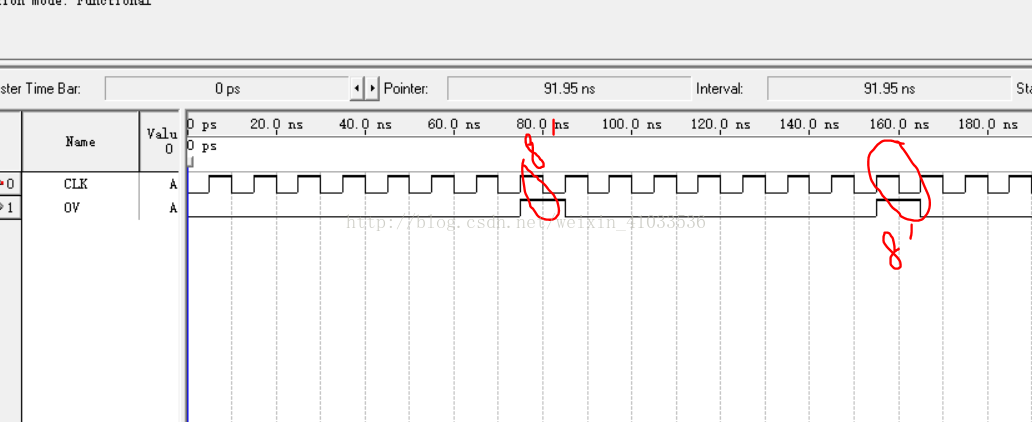
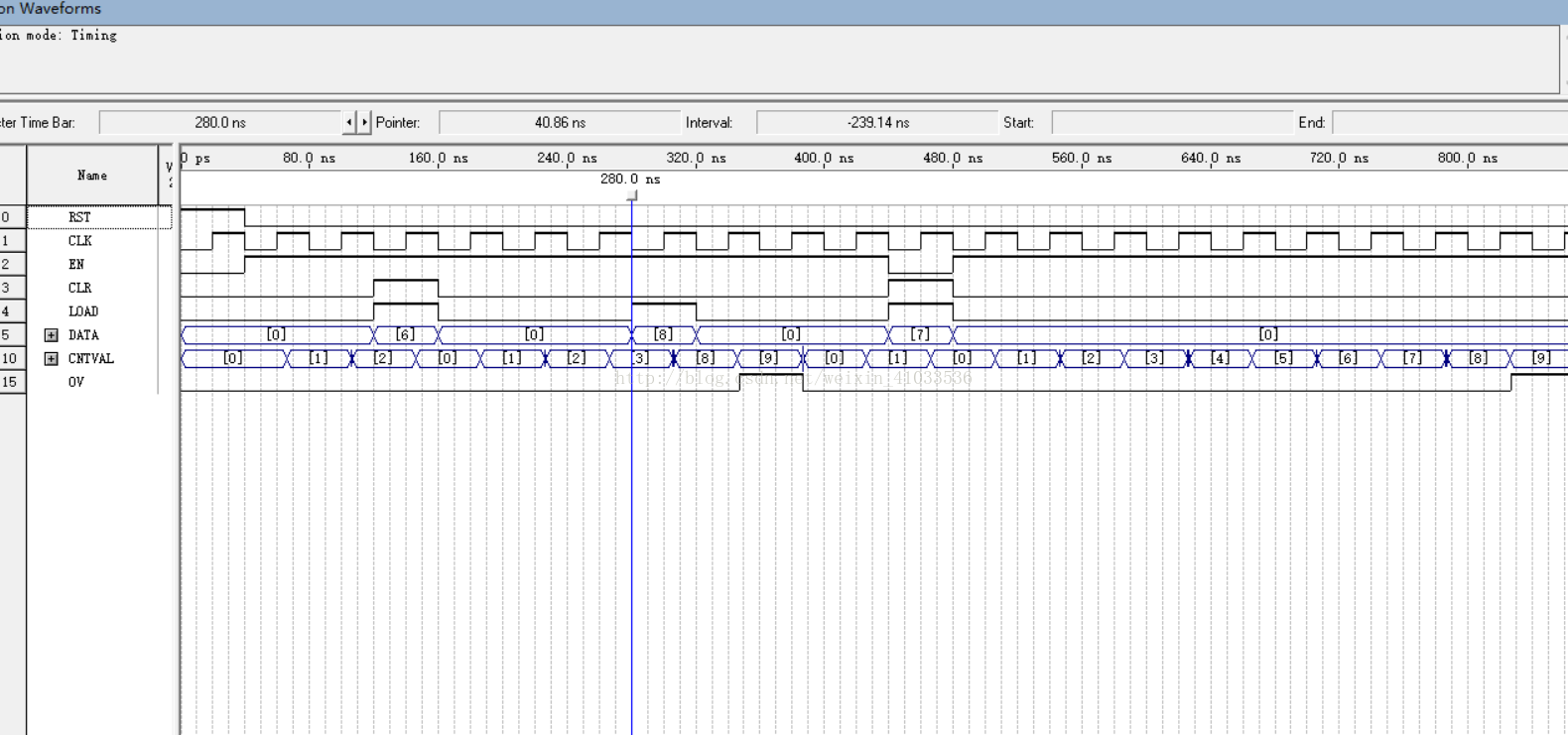
波形仿真结果如下:
只有CLK和Overflow信号的简单计数器
改变三种信号优先级的计数器
10. 设计一个用于识别2进制序列“1011”的状态机
(1) 基本要求:电路每个时钟周期输入1比特数据,当捕获到1011的时钟周期,电路输出1,否则输出0;使用序列101011010作为输出的测试序列;
(2) 扩展要求:给你的电路添加输入使能端口,只有输入使能EN为1的时钟周期,才从输入的数据端口向内部获取1比特序列数据。
实验分析:因为要捕获的是“1011”序列,从最低位开始进行匹配,匹配成功跳转到下一状态匹配更高一位,只要有一位匹配错误就应该跳转至状态0重新开始。而加上使能信号后,只有EN为1才从输入端读入输入数据进行匹配。
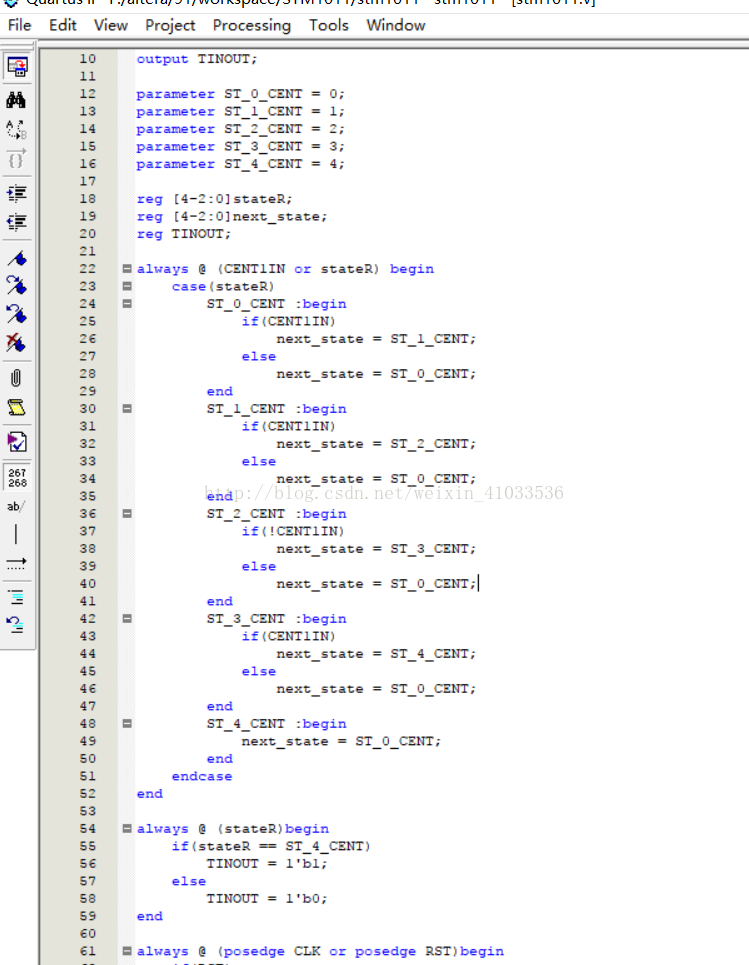
实验代码设计如下:
基本要求的状态机
带使能信号的状态机
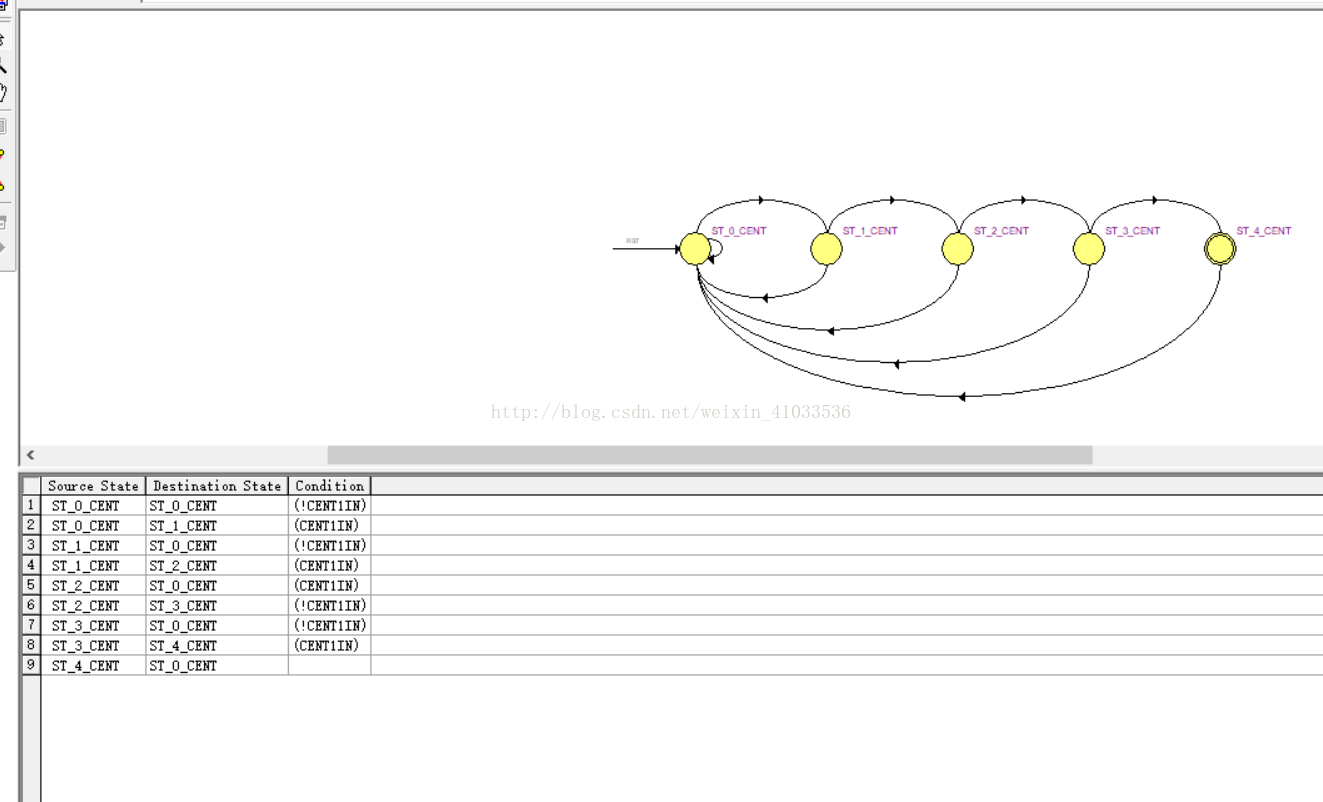
状态转移图及表达式如下:
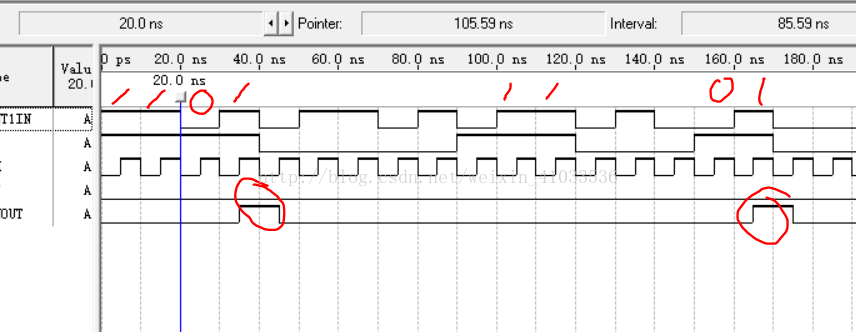
波形仿真结果如下:
基本要求的状态机
带使能信号的状态机
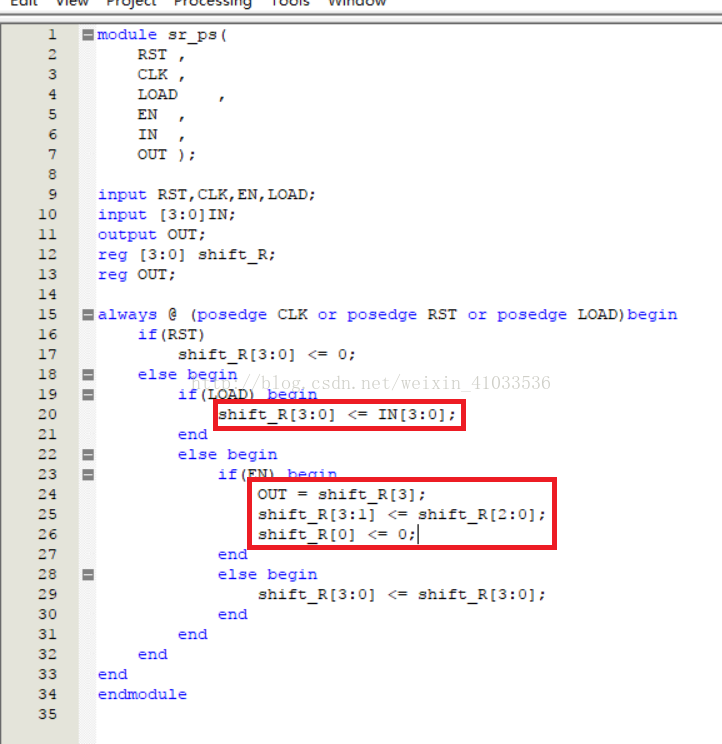
11. 设计一个如本节“电路描述”部分的“带加载使能和移位使能的并入串出”的移位寄存器,电路的RTL结构图如“电路描述”部分的RTL结构图所示。
实验分析:所谓“串入并出”的移位寄存器,及输入一个1位输入信号,移位寄存器将这个一位数据存入第0位,并将原本的后3位一同前移1位,最后从高到低并行输出四位数据。而“并入串出”的移位寄存器是指,输入一个4位输入信号,存入移位寄存器,若移位使能有效,则将最高位输出,移位寄存器后三3同时前移1位,最低位存入0;若加载时能有效,则从输入端重新读入4位数据。
实验代码设计如下:
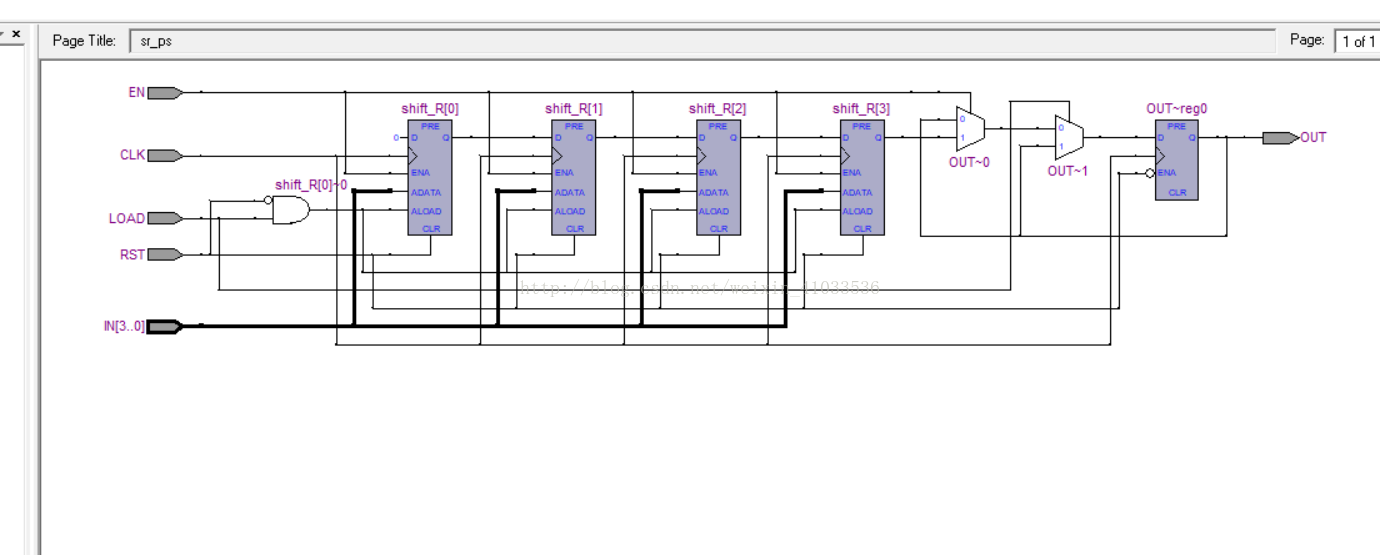
RTL视图如下:
波形仿真结果如下:
实验小结:
本次实验共分为11个小的实验,通过Verilog代码模拟了各种逻辑组合电路的基本原理。通过例子实验和自主进行的实验可以发现,任何一个复杂的组合电路都可以拆分成许多简单的基本电路,通过熟练这些基本电路的Verilog代码编写,并在每次实验前都先对要完成的项目进行拆分与简化,重视RTL视图,就可以实现各类大型项目的编写。
同时,在实验过程中自己也检验了对Verilog代码的使用熟练度与理解,如[3:0]即声明一个最高位为第三位最低位为第零位的变量、if...else语句最好使用begin...end括起来,以及一些其他的代码规范。这些都对之后的开发仿真工作有极大的提示帮助。