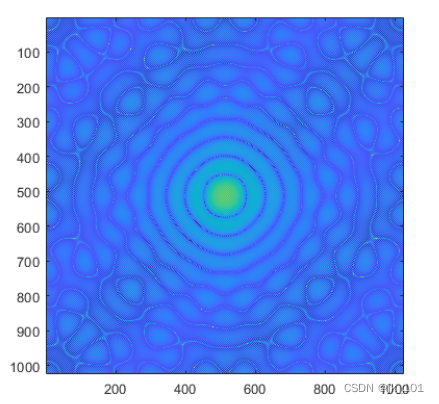
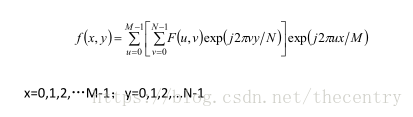一：二维傅里叶变换的数学原理

1.2D离散傅里叶公式解释：

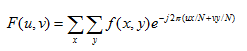
那么，其F(u,v) 本质就是：

                                            

后续说明时的”频域”均指的其傅里叶功率谱，后面为了演示方便，所有频域图均经过了fftshift移动到中心位置。

2.2D傅里叶频率图理解：

1).二维cos函数及其F(u,v)

A.图像：cos(0.3x+0.3y)，其频域上出现2个极值点，及对应其cos(0.3x+0.3y)函数本身

B.图像：cos(0.3x+0.3y)+ cos(0.3x-0.3y)，该图像表现为规则点阵，其傅里叶频域图上则按预期的出现4个极值点

C.图像：cos(0.3x+0.3y)+ cos(0.3x-0.3y)+cos(0.6x+0.4y)，同理，会出现6个极值点

2).F(u,v)图意义

F(u,v)图像每一点意义可用如下图清晰解释[1]：

即频谱图像的每一点即表示一个cos函数，点的位置即表示该函数的w1和w2。

以下我们通过使用有限个cos函数图像来进行合成lena图像

其中傅里叶频谱图上点的强度表示了求和时的cos函数的权值，越白表示权值越大。从上图可看到，仅使用低频部分的几十个cos函数已基本合成了lena。

二.2-D FFT主要性质

1.理解2D-FFT的平移不变性:

我们用1维公式进行推导：

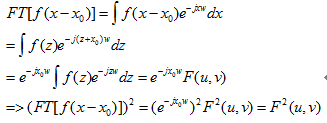
所以不管1D，还是2D，平移不影响频域功率图，我们通过以下事例来说明该结论

 

     

2.理解2D-FFT的旋转同步性:

1)旋转同步性的数学推导：

可见f(x,y)与旋转 后的f(x’,y’)的频域图形也同步为 的偏差

2)旋转同步性的图示：

我们通过如下水平与逆时针15°的图像作为说明

   

三.经典基本图像的频谱图

1.高斯图像的傅里叶变化：

1)高斯点频域的数学推导

为便于推导，我们选择1维高斯函数作为数学说明

即高斯点的频域图还是高斯点，只是方差对应成倒数关系，即时域中高斯函数方差越大，对应频域图像的方差越小。

我们可以想一下高斯低通滤波器，当我们想要一个非常低通的滤波器时：

    频域：要求截止频率很低，也即要该滤波器的非常接近中心，视觉上则表现为高斯函数方差很大。

    时域：需要一个非常低的低通滤波器，我们则要求其核半径非常大，该滤波器视觉上表现为方差非常小。

2)高斯点频域图示

我们通过2个方差不同的高斯点进行说明

     

3)多个高斯点的频域图

该结论同样适合于任何其他图形的叠加，我们通过不同位移量的高斯点进行说明：

       

2.box(sinc)图像的傅里叶变化：

1)box函数数学说明

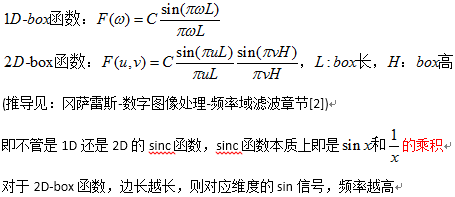
2)box函数频域图像说明

我们通过不同长宽的数据进行说明：

可以看到，长和高分别变化，会引起频域上其对应的sin相应变化

3)Box函数特例：直线函数

直线可看成box函数的特例，即长宽比特别大的：边长越长，对应方向块效应频率越高；边长越短，对应方块效应频率越低。

A.宽变换：

可以看到，随着宽的变短，水平方向的频率不断变少，最终变成频率为0的常数sin

B.长变化：

可以看到，随着长不断边长，垂直方向线段频率逐渐变高，最终达到1pixel的极限

3.圆域图像的傅里叶变化：

1)圆域函数的数学说明

圆域函数的FT推导需要用到贝塞尔公式，比较复杂。但是可以大致这样认为：

我们可以将圆看成有限个直线的求和，由

结合FT的可加性、旋转同步性、直线函数频域图像，可以推测圆域函数的FT应该类似于直线一样是成周期性的衰减圆环状。

和直线同样性质，圆越大，圆环的频率越高，我们通过如下不同半径的圆进行说明

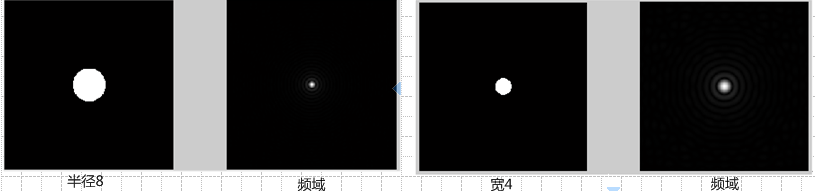
2)圆环函数

四.部分真实图像的傅里叶变化：

1.牛顿环：

FT后，仍然是环状，因为牛顿环可以看成多个圆域函数的线性叠加

2.特斯拉标记：

2.1 频域与图像对应

该图像主要以几条曲线构成，可以很容易发现该频域图像与其时域的对应关系。

2.2 图像边缘对频谱的影响

可以看到上面2.1中的特斯拉图像取反前后，频域的图像几乎没变化，这符合预期，因为关键的边界信息是相同的。但是取反后中间垂直的2条亮线没有了，这个是由于边缘导致。

当背景有颜色时，图像的边缘即构成水平和垂直的阶跃信号，所以我们实际使用的大部分图像，几乎都可以看到其频谱图出现中间2条周期亮线的情况。

2.3 如何消除图像边缘对频谱的影响

图像边缘的阶跃效应会导致频域图中，出现中心两条带旁瓣的亮线，这有时会干扰我们对水平/垂直规律信号的分析。

我们对lena进行FT，如预期的，中心出现亮线。

接下来我们对边缘进行衰减，即可大大降低边缘阶跃效应。可以看到，边缘衰减后，FT图的中心亮线几乎消失。

3.指纹图像：

指纹的纹路是在一个较窄带的范围的纹路信号，其图像可以近似成有限个一定周期、不同方向的cos函数叠加，所以指纹的频谱能量会主要集中在一个环带范围内。下图可以明显看到，其频域图中有一个较亮的环状带。

 

特别说明：

[1].知乎-阿姆斯特朗

[2].数字图像处理-冈萨雷斯

由于原稿是在word中编辑，文中带有公式的段落是直接贴图，可能导致排布不对齐，见谅。