目录

1.相关基础知识参考链接

2.二维傅里叶变换作用简介

3.FFTW二维傅里叶变换输出分析

（1）原始输出数据​

（2）频谱中心化后的输出数据

4.频谱图绘制

5.二维傅里叶变换逆变换

6.从输出结果中分离各平面波并画出波形平面图

7.归一化方法及实现

8.频谱中心化实现

9. 图像（R，G，B）彩图二维傅里叶变换

10.二维傅里叶变换FFTW使用说明

11.r-c中正变换输出数据长度

---

1.相关基础知识参考链接

离散傅里叶变换（DFT）基础知识理解参考：

深入理解离散傅里叶变换(DFT) - 知乎

FFTW库基本使用参考：

FFTW3学习笔记2：FFTW（快速傅里叶变换）中文参考 - 爱国呐 - 博客园

关于FFTW库的使用和离散傅里叶变换的基础知识参考上述两篇优秀文章即可，我学习过程中也是参考上述文章进行学习的，此文着重于二维傅里叶变换方面FFTW库在实践过程中的问题及解决。

2.二维傅里叶变换作用简介

二维傅里叶变换：将1个图像分解为若干复平面波之和，将图像从空间域转至频域

平面波：在一个方向上存在一个正弦函数，在法线方向上将其拉伸（正弦平面波）

表示平面波所需参数：                                                        平面波举例：

        

 二维傅里叶变换过程图示：

将输入图像分解为若干平面波之和，图像每个点像素由RGB组成，FFTW输入计算时，需将RGB变为灰度值

平面波合成图解：

  

3.FFTW二维傅里叶变换输出分析

输出结果一半在分析前需进行频谱中心化，这样讲有助于分析，下面将分别记录。

（1）原始输出数据

• FFTW二维傅里叶变换输出为和输入图像行列数（m，n）相同的元素为复数的矩阵。
• 各复数元素，幅值·相位·频率 均可由复数的实部虚部计算得到，平面波的方向则由当前元素和所在区域的低频顶点（即直流）在数组中的距离和组成的向量来表示。如图中箭头所指方向，为（a+bi）所代表平面波的方向，由（a+bi）所在的点和4区域低频顶点所形成的向量代表方向
• 矩阵整体以行列中心为分界线，将矩阵分为4个区域。1区和4区对应，2区和3区对应，对应区域中的复数值，实部相同，虚部互为相反数。
• 此时输出各区域中，低频分量在四角部分，高频分量在中心部分。

（2）频谱中心化后的输出数据

频谱中心化：将4个区域的顺序对调（14对调  23对调），从而使输出低频在中心，高频在四周，这样有助于分析，更符合人们观察习惯。频谱中心化后，中心低频就是直流。建议第二种方法，第一种方法中心不确定，易出错

频谱中心化对各平面波幅度，相位，频率，方向均无影响，此时方向为矩阵中心指向元素所在位置，无影响。

注意：频谱中心化对输出数据的顺序进行了修改，若需要进行逆变换，则需再次进行一次频谱中心化操作，使数据恢复原始状态，否则逆变换结果有误。

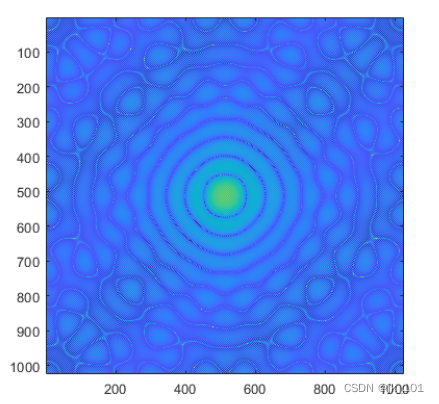
4.频谱图绘制

频谱图：计算中心化后各点的幅值，对幅值进行归一化，将其大小控制在0-255之间，并以此值作为灰度值，绘制灰度图。

归一化目的：灰度图各点数值范围为0-255，而输出各点幅值数据大小并非在此范围中，即使全部在此范围中，也并非均匀分布，上述情况均会使成图效果低下，导致全黑或全白或其他情况。归一化后将数值范围限制在0-255中，并将数值按大小比例分布在范围内，成图效果好。

效果如下：（绘图使用Opencv）

               原图：                                                        中心化归一化频谱图：

                        

                    未中心化归一化频谱图：                                        中心化未归一化频谱图：

                                          

 以下几种情况会导致绘图结果不同：

• 灰度转换公式中RGB各通道所占比参数不同，从而直接影响之后的结果
• 归一化过程中方式不同，归一化方法不唯一，不同方法导致灰度值不同，可能导致过亮过暗
• 某些实现过程可能会忽略部分较小值，只关注主体，从而使图像展示不同

5.二维傅里叶变换逆变换

二维傅里叶逆变换：将图像由频域转为空间域，即将各平面波进行合成，从而形成图像

效果如下：

                                      原图：                                                                逆变换：

                            

                                       原图：                                                                  逆变换：

                                   

原图为RGB三色图，但由于在正向变换前将图片变为了灰度图，导致逆变换后的结果仍为灰度图，若想要对RGB图像变换而非灰度图，则对R，G，B三通道数值单独进行正变换，再依次逆变换后，将得到的三组数据合成RGB三色数据，即可得到原始三色图

 逆变换注意：

• 若正向变换过程中使用了频谱中心化，则在逆变换结果中需再进行一次频谱中心化以抵消之前的变换，得到正确的图像，否则图像对应区域互相颠倒
• Fftw库逆变换得到的结果需除以总样本数（m*n），才能得到正确的图像。若不除以则数值过大导致图像为全白（超出显示最大值，均按最大值处理）

6.从输出结果中分离各平面波并画出波形平面图

二维傅里叶变换的结果中每一个点代表一种平面波，每对关于中心对称的一对数值点，经过逆变换后，可得到相应平面波。

中心：输出结果的中心不一定在矩阵中心

如：（5，5）的矩阵中心为（3，3），但FFTW中二维傅里叶输出结果的中心可能在（3，4）（4，4）等（5，5）附近的点上（可能是小数），判断中心点需比较对角数据，从而计算出中心点的具体所在位置，若中心点找错，即导致所选的两对频点并不对称，逆变换的结果也就是错误的

对称频点：实部相同，虚部互为相反数

 例：

原图：大小（318*318）（0-317）

 

下图对应数据分别为左上角和右下角中5*5大小的输出结果

图中紫色部分数据相同，即（1，1）与（317，317）相同，而不是（0，0）与（317，317）相同，第0列和第0行无对称点

即对称点为（159，159），且第0列和第0行无对称点

成图流程：

1. 1.  选定需要逆变换的一对频点，并将其余频点数据均置为0，才可正确显示此频点对应的平面
2. 2.  若正变换进行过频谱中心化，则需再进行一次频谱中心化
3. 3.  逆变换得到的结果需进行归一化处理，将数值固定在0-255范围内。（整体逆变换无需进行归一
4. 化，因为各平面波之间数据互相作用，使得最终结果范围再可输出区间内，而单独对一个平面波逆
5. 变换，此平面波的幅值可能过大或过小，此平面波只是原本图片的组成部分之一，直接输出结果通
6. 常无法观察，全黑或全白/数值过小或数值过大，因此需要进行归一化处理）
7. 注意：只有两点对称进行逆变换，变换结果的虚部才会近似为0可忽略，才可得到正确图像

效果如下：

​​​

！若所选取的频点对应频率过高，会导致一个像素内多次数据重复，从而使结果无法正确显示！

7.归一化方法及实现

流程：

1.求出各点幅值

2.对各点幅值加一并进行1og运算，减小范围（缩小数据分布间隔，使分布更均匀，成图效果更好）

3.求出2中最大值最小值之差，并用255除以其值得到步长scale

4.用最小值乘以步长得到偏差

5.各值乘以步长减去偏差即可

实现（使用Opencv）：

double min1 = 0.0, max1 = 0.0;
minMaxLoc(backward, &min1, &max1);
double scale1 = 255 / (max1 - min1);
double shift1 = -min1 * scale1;
Mat myImage1;
convertScaleAbs(backward, myImage1, scale1, shift1);// 此代码未进行log过程，若有需要可添加
// 相关函数为Opencv中相关函数

8.频谱中心化实现

频谱中心化实现方法之前已经提及，此处给出实现：

互换区域中心化：

void fftshift(Mat source, Mat& dest)
{int row = source.rows;int col = source.cols;int halfRow = row / 2;int halfCol = col / 2;int temp = 0;for (size_t j = 0; j < row; j++){temp = (j + halfRow) % row;for (size_t i = 0; i < col; i++){*dest.ptr<float>(temp, i) = *source.ptr<float>(j, i);}}source = dest.clone();for (size_t i = 0; i < col; i++){temp = (i + halfCol) % col;for (size_t j = 0; j < row; j++){*dest.ptr<float>(j, temp) = *source.ptr<float>(j, i);}}}

输入乘以 （建议）：

void fftshift2(Mat source, Mat& dest)
{int row = source.rows;int col = source.cols;int halfRow = row / 2;int halfCol = col / 2;for (int j = 0; j < col; j++){for (int i = 0; i < row; i++){*dest.ptr<float>(i, j) = *source.ptr<float>(i, j) * (pow(-1, i + j));}}
}

9. 图像（R，G，B）彩图二维傅里叶变换

将R，G，B各单通道数据拿出分别进行变换，逆变换也是分别进行，最后再将各单通道数据组合

效果如下：

                                   原图：                                                        B通道正变换：

                             

                        G通道正变换：                                                        R通道正变换：

                                

                        B通道逆变换：                                                        G通道逆变换：

                                

                                R通道逆变换：                                        （B，G，R）逆变换组合：

                        ​​​​​​​        

10.二维傅里叶变换FFTW使用说明

1.二维图像输入应使用二维数组，但fftw中二维输入仍以一维数组方式存储，在调用方法时，指定二维输入的行列，以便于分割

2.复数类型中实数输入需转变为复数，虚部为0

3.空间申请需使用fftw内部给定的类型，防止内存出现错误

4.方法的创建放在输入赋值之前

5.使用fftw_destroy_plan和fftw_free释放方法和输入输出数据所占的空间

6.同一方法在不修改输入输出大小的前提下，可更改内部数据重复多次变换。

11.r-c中正变换输出数据长度

1.Fftw中所有rtc/ctr函数将正逆变换分开，输入是n个实数，而输出是n/2+1 个复数，输出只有n/2+1位，申请n空间，未初始化则n/2+1位后面则无数据，若未初始化则后面数据未知，因此应只为输出申请n/2+1空间或对n空间输出进行初始化即可（即所有rtc/ctr函数正变换输出只有n/2+1个数据有效）

分析时需注意所有rtc/ctr函数的正变换输出有效位数，切勿使用无效数据

2.非rtc/ctr函数的正变换n/2+1之后的数据为之前数据的对称，故使用此方法时可分析全部数据

3.所有rtc/ctr函数生成方法时仍需指定完整长度数值

未初始化：

初始化0：

初始化1：