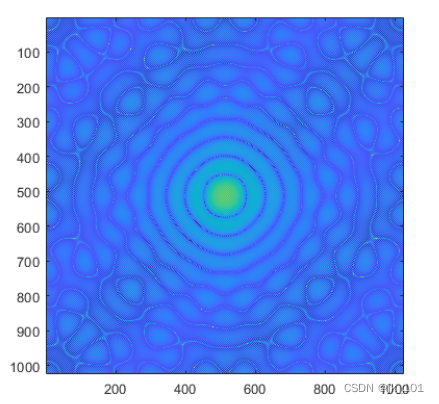
在处理二维矩阵时,常想着如何把时域转换到频域来处理,因此翻来了以往数分里面的常用的傅里叶(Fourier Transform);
(Notes:一下公式中 M,N分别为二维矩阵的列数和行数,f(x,y) 代表改二维矩阵,F(u,v)为转换后的矩阵);
I. 傅里叶变换的公式:

拆分到这里,我也很开心的掏出祖传的Matlab写了几行代码来实现:
function [Fuv] = Myft2(fxy)[N,M,dim] = size(fxy);if dim > 1txy = double((rgb2gray(fxy)))/255;elsetxy = double(fxy)/255;end[U,V] = meshgrid(0:M-1,0:N-1);Gxv = zeros(N,M);for y = 1:NA2 = txy.*exp(-2*pi*1i * (y-1)*V./N);Gxv(y,:) = sum(A2,1);endFuv = zeros(N,M);for x = 1:MA1 = Gxv .* exp(-2*pi*1i * (x-1)*U ./ M);Fuv(:,x) = sum(A1,2);end
然后与matlab自带函数fft2 做组对比:
clear;clc;
Lena = imread('lena.jpg');tic;
tSrc_fft = Lena;
Fmy = Myft2(tSrc_fft);
sp1 = toc;
tic;
if size(Lena,3) > 1tSrc_mat = double((rgb2gray(Lena)))/255;
elsetSrc_mat = double(Lena)/255;
end
Fmatlab = fft2(tSrc_mat);
sp2=toc;
tE = isempty(find(abs(Fmatlab - Fmy) > 0.01, 1));
disp(['是否为空:',num2str(tE)]);
disp(['时间长(s):',num2str(sp1 - sp2)]);
但是时间却相差甚远:
看了看原公式,想了想如果把上述代码转换成Matlab 矩阵运算是不是会提速。然后就实际行动起来:
上面公式可以转换成 F = g1* f *g2;(矩阵与代码如下:)

function [Fuv ] = Myft2(fxy )[N,M,dim] = size(fxy);if dim > 1txy = double((rgb2gray(fxy)))/255;elsetxy = double(fxy)/255;end[Vx,Vy] = meshgrid(0:N-1,0:N-1);G1 = exp(-1i*2*pi .*(Vx.*Vy)./N);[Ux,Uy] = meshgrid(0:M-1,0:M-1);G2 = exp(-1i*2*pi .*(Ux.*Uy)./M);Fuv = G1 * txy * G2;
重复上面的对比:
果然Matlb矩阵计算还是有优势的,效果看起来还可以;
II. 傅里叶逆变换公式:

用同样的方式,写傅里叶逆变换的代码,即可获取同样的效果,这里就只贴上公式了;下一期打算做一下基于fft的高通滤波