1. 偏向锁分析

回顾轻量级锁

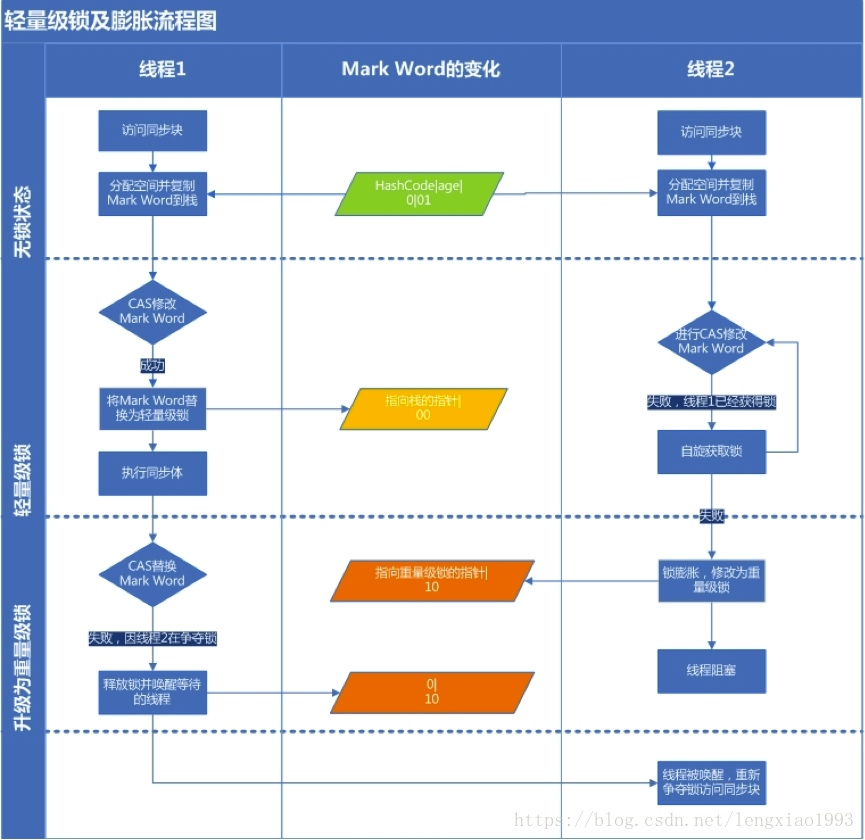
在上文 Java并发 | 18.[锁机制] 轻量级锁（CAS+自旋锁）中对轻量级锁进行过解析，实现轻量级锁，不仅上锁解锁时要频繁进行CAS操作，且如果频繁出现重入锁，则会有很多次没有意义的CAS操作。

偏向锁的优势

偏向锁适用于 从始至终都只有一个线程在运行的情况。它只是通过CAS在 obj 的 MarkWord 中标记了线程ID，每次 获取锁，只需要比对线程ID是否匹配即可。

相比轻量级锁，偏向锁认为由始至终都只有一个线程在运行，所以没有解锁的过程，只是在 MarkWord 中标记线程ID，更加节约性能。每次都核对一下ID是否一致，一致则执行，不一致则考虑升级。

2. 偏向锁（CAS）

2.1. 偏向锁流程概述

• [第一个线程上锁] 线程 t1 访问 obj 的MarkWord，发现它并没有被任何线程绑定，于是将自己的线程ID标记上去；

• [t1再次执行] t1 执行结束后不会执行任何解锁操作。当它再次执行代码块时，发现线程ID与自己的匹配，于是直接执行；

• [t2竞争锁] 若某个时刻有 t2 访问 obj 的 MarkWord，发现它已被线程t1绑定，那么会在一个全局安全点停止t1，并检查t1的状态：

  • 若 t1 已停止，则认为不会产生竞争，t2 将 MarkWord 的线程ID换成自己的；
  • 若 t1 仍活跃，说明产生了竞争，则会将锁升级为轻量级锁。

  

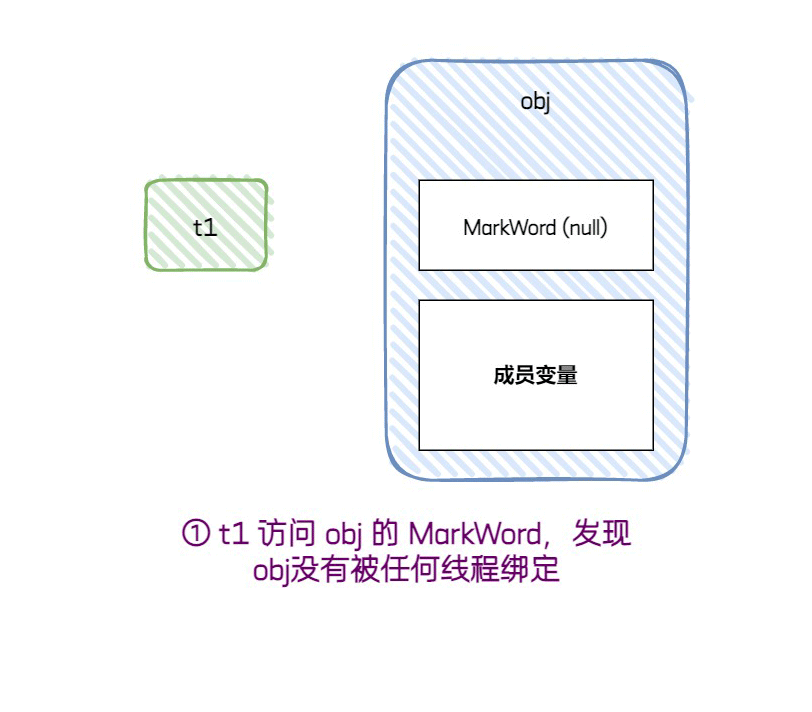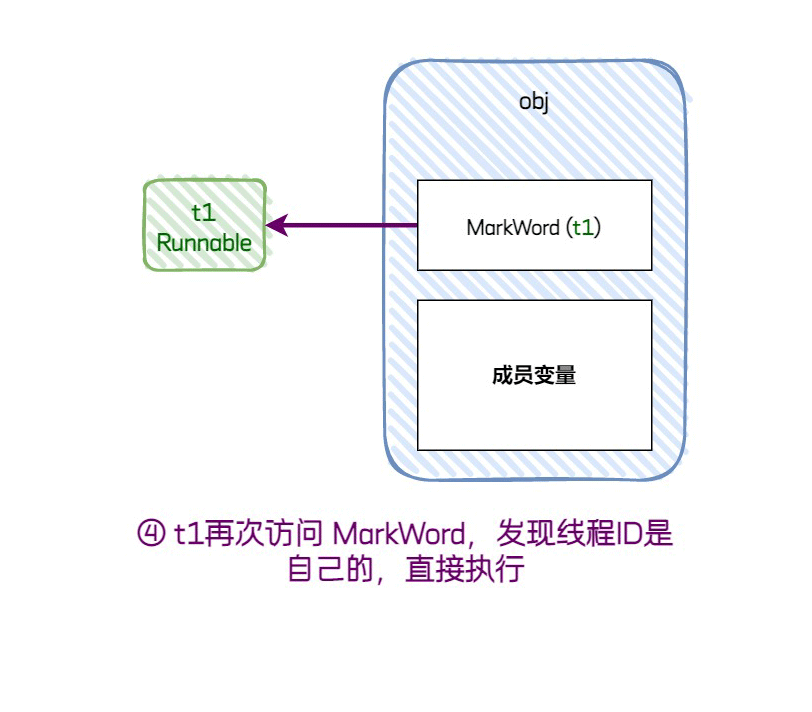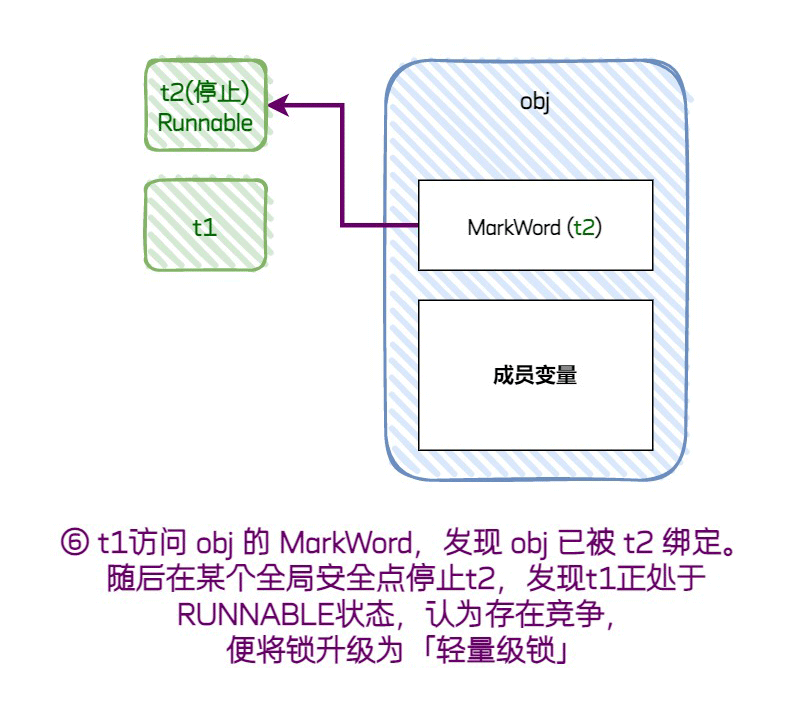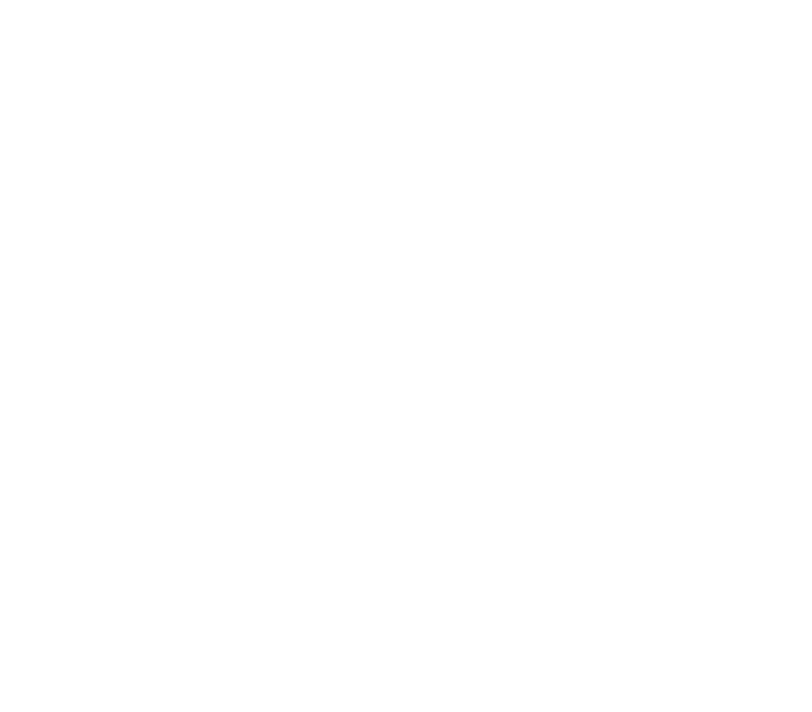
2.2. 锁升级

t2 与 t1 发生锁竞争，在停止 t1 后若发现它依旧活跃，就会将「偏向锁」升级成「轻量级锁」，此时 t1 将被唤醒并继续执行，而 t2 则会与 obj 的 MarkWord 发生 CAS，待 t1 执行完毕，t2 就会以轻量级锁的方式开始执行代码。

参考资料

[文章] 从偏向锁是如何升级到重量级锁的-偏向锁