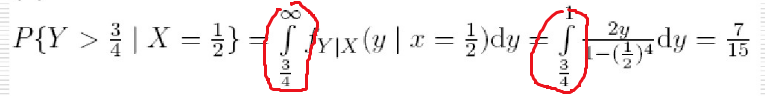考虑第一种情形的条件高斯分布。假设 X 是一个满足高斯分布  的 D 维向量,我们把 X 分作两个子集 Xa 和 Xb 。不失一般性,我们记 Xa 为 X 的前 M 个元素, Xb 为剩下 D-M 个元素,即
的 D 维向量,我们把 X 分作两个子集 Xa 和 Xb 。不失一般性,我们记 Xa 为 X 的前 M 个元素, Xb 为剩下 D-M 个元素,即

 。在此需要强调的是,
。在此需要强调的是,  不是简单的给
不是简单的给  取逆。事实上,我们将会考察分块矩阵的逆和其分块的逆之间的关系。
取逆。事实上,我们将会考察分块矩阵的逆和其分块的逆之间的关系。
首先,我们来寻求条件概率 的表示。根据概率的乘法性质,得到该条件概率可以简单地通过用 Xb 的观测值来修正联合概率
的表示。根据概率的乘法性质,得到该条件概率可以简单地通过用 Xb 的观测值来修正联合概率  并归一化其结果表示从而得到合理的 Xa 上的合理概率分布。我们不是具体地实行归一化,而是采用高效地方法,即考虑( 2.44 )给出的高斯分布中指数的二次形然后在计算的最后恢复归一化系数。使用划分( 2.65 ),( 2.66 )和( 2.69 )得到
并归一化其结果表示从而得到合理的 Xa 上的合理概率分布。我们不是具体地实行归一化,而是采用高效地方法,即考虑( 2.44 )给出的高斯分布中指数的二次形然后在计算的最后恢复归一化系数。使用划分( 2.65 ),( 2.66 )和( 2.69 )得到


( 2.73 )和( 2.75 )的结果是由初始联合分布 的精度矩阵中的分块项表示的。我们同样可以用协方差矩阵的对应分块项来表示这些结果。为了实现这个,我们利用了以下分块矩阵的逆的恒等式
的精度矩阵中的分块项表示的。我们同样可以用协方差矩阵的对应分块项来表示这些结果。为了实现这个,我们利用了以下分块矩阵的逆的恒等式


 的大小称作( 2.76 )左边矩阵相对于子矩阵 D 的舒尔补( Schur complement )。采用定义
的大小称作( 2.76 )左边矩阵相对于子矩阵 D 的舒尔补( Schur complement )。采用定义


我们还定义期望向量  的分块
的分块

及协方差矩阵  的分块
的分块

注意到协方差的对称性  隐含着
隐含着  和
和  也是对称的,以及
也是对称的,以及  。
。
在许多情形下,使用协方差矩阵的逆会更加方便

首先,我们来寻求条件概率
可见这是一个关于 Xa 的函数,而且是二次形式,因此,对应的条件分布  将是高斯分布。因为,这种分布(高斯分布)完全由期望和方差表征,所以,我们的目标是检查(2.70)的期望和方差的等价表示。
将是高斯分布。因为,这种分布(高斯分布)完全由期望和方差表征,所以,我们的目标是检查(2.70)的期望和方差的等价表示。
它是一个与高斯分布相联系的极普通的例子,有时称为“完全平方”,其中给了我们高斯分布中指数项中的二次形式,以及我们需要确定对应的期望和方差。该问题可以直接通过标记普通高斯分布 的指数可以记为
的指数可以记为

这里的“ const ”表示独立于 X 的项,而且我们利用了 的对称性。因此,如果将普通的二项形式并且将它表示为( 2.71 )右边的形式,那么我们可以立即将 X 的二次项的系数等同于协方差矩阵的逆
的对称性。因此,如果将普通的二项形式并且将它表示为( 2.71 )右边的形式,那么我们可以立即将 X 的二次项的系数等同于协方差矩阵的逆  而且 X 的线性项系数等同于
而且 X 的线性项系数等同于  ,由此我们可以获得
,由此我们可以获得  。
。
它是一个与高斯分布相联系的极普通的例子,有时称为“完全平方”,其中给了我们高斯分布中指数项中的二次形式,以及我们需要确定对应的期望和方差。该问题可以直接通过标记普通高斯分布
这里的“ const ”表示独立于 X 的项,而且我们利用了
现在将该步骤应用于条件高斯分布  它的指数项的二次形式由( 2.70 )给出。我们分别用
它的指数项的二次形式由( 2.70 )给出。我们分别用
 和
和  表示该分布的期望和方差。考虑该函数依赖于 Xa ,对于 Xb 则视为常数。如果我们将 Xa 所有二次项提出,则得到
表示该分布的期望和方差。考虑该函数依赖于 Xa ,对于 Xb 则视为常数。如果我们将 Xa 所有二次项提出,则得到

据此可以立即总结出  的协方差矩阵(精度矩阵的逆)为
的协方差矩阵(精度矩阵的逆)为

( 2.73 )和( 2.75 )的结果是由初始联合分布
通过这些我们可以获得条件分布  的期望和方差的等式如下
的期望和方差的等式如下

比较( 2.73 )和( 2.82 ),可以当采用精度矩阵的分块项来表示条件概率  相对于采用协方差矩阵的分块项更加简单。注意,条件概率
相对于采用协方差矩阵的分块项更加简单。注意,条件概率  的期望(由( 2.81 给出)),是 Xb 的线性函数,而协方差(由( 2.82 给出))独立于 Xa 。这代表了一种线性高斯模型的例子。
的期望(由( 2.81 给出)),是 Xb 的线性函数,而协方差(由( 2.82 给出))独立于 Xa 。这代表了一种线性高斯模型的例子。  是高斯分布,那么条件高斯分布
是高斯分布,那么条件高斯分布  也是高斯分布。现在我们回到如下的边缘分布的讨论,
也是高斯分布。现在我们回到如下的边缘分布的讨论,

2.3.2边缘高斯分布
我们已经见到如果联合分布 我们将看到,它同样是高斯分布。同样,我们的策略关注与联合分布的二次形式指数项从而确定边缘分布  的期望和方差。
的期望和方差。 
该积分是在非归一化的高斯分布上的积分,所以结果将会和其系数有关。通过( 2.43 )给出的归一化高斯形式我们可以知道系数和均值独立,并且只依赖于协方差矩阵的行列式。因此,对 Xb 配方,我们可以积出 Xb 而分布( 2.84 )左边的依赖于 Xa 剩余项是( 2.84 )右边的最后一项其中 m 由( 2.85 )给出。结合该项以及( 2.70 )的依赖于 Xa 的剩余项,得到

这里“ const ”表示数值独立于 Xa 。再次,通过同( 2.71 )比较,可以发现边缘分布 的协方差矩阵是
的协方差矩阵是

该积分是在非归一化的高斯分布上的积分,所以结果将会和其系数有关。通过( 2.43 )给出的归一化高斯形式我们可以知道系数和均值独立,并且只依赖于协方差矩阵的行列式。因此,对 Xb 配方,我们可以积出 Xb 而分布( 2.84 )左边的依赖于 Xa 剩余项是( 2.84 )右边的最后一项其中 m 由( 2.85 )给出。结合该项以及( 2.70 )的依赖于 Xa 的剩余项,得到
这里“ const ”表示数值独立于 Xa 。再次,通过同( 2.71 )比较,可以发现边缘分布