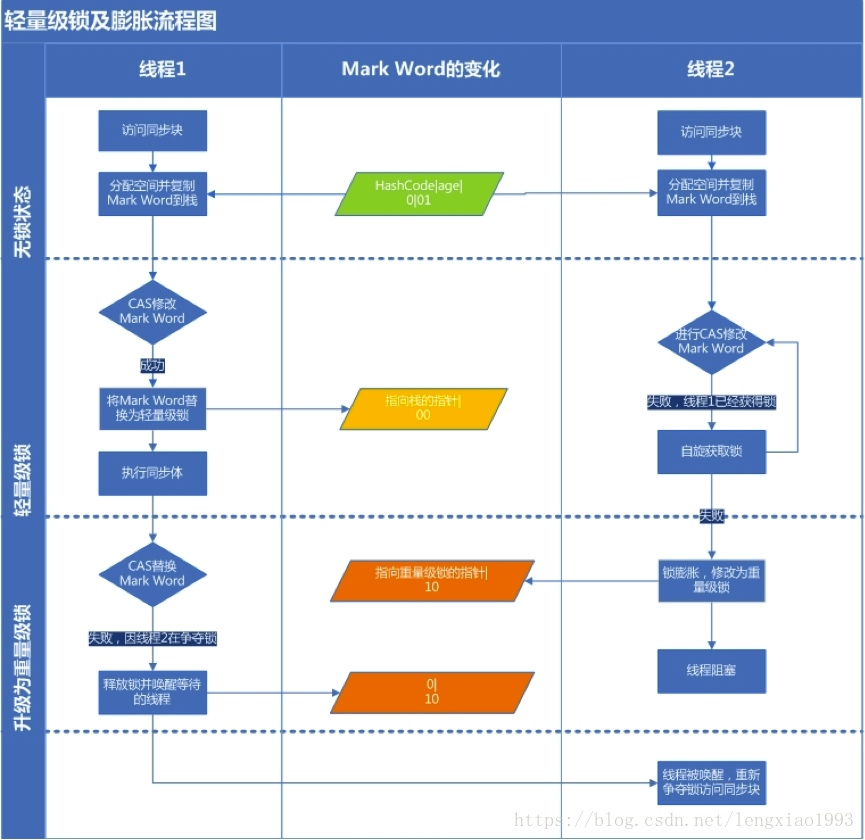
所谓的偏向,就是偏心,即锁会偏向于当前已经占有锁的线程 。
大部分情况是没有竞争的(某个同步块大多数情况都不会出现多线程同时竞争锁),所以可以通过偏向来提高性能。即在无竞争时,之前获得锁的线程再次获得锁时,会判断是否偏向锁指向我,那么该线程将不用再次获得锁,直接就可以进入同步块。
偏向锁的实施就是将对象头Mark的标记设置为偏向,并将线程ID写入对象头Mark
当其他线程请求相同的锁时,偏向模式结束
JVM默认启用偏向锁 -XX:+UseBiasedLocking
在竞争激烈的场合,偏向锁会增加系统负担(每次都要加一次是否偏向的判断)
代码例子

public class TestUseBisaedUsing {public static List<Integer> numberList = new Vector<Integer>();public static void main(String[] args) throws InterruptedException {long begin = System.currentTimeMillis();int count = 0;int startnum = 0;while (count < 10000000) {numberList.add(startnum);startnum += 2;count++;}long end = System.currentTimeMillis();System.out.println(end - begin);}
Vector是一个线程安全的类,内部使用了锁机制。每次add都会进行锁请求。上述代码只有main一个线程再反复add请求锁。
使用如下的JVM参数来设置偏向锁:
-XX:+UseBiasedLocking -XX:BiasedLockingStartupDelay=0BiasedLockingStartupDelay表示系统启动几秒钟后启用偏向锁。默认为4秒,原因在于,系统刚启动时,一般数据竞争是比较激烈的,此时启用偏向锁会降低性能。
由于这里为了测试偏向锁的性能,所以把延迟偏向锁的时间设置为0。
可以看到运行时间为423ms


下面关闭偏向锁:
-XX:-UseBiasedLocking

输出699ms
一般在无竞争时,启用偏向锁性能会提高5%左右。