摘要:本文主要介绍二维随机变量的联合分布律、边缘分布律和条件分布律之间的关系,并以矿山事故为例,强化对三者关系的认识。
一、联合分布律、边缘分布律和条件分布律之间的关系
1、若已知(X, Y)的联合分布率 => 可以求出X的边缘分布律和Y的边缘分布率
● X的边缘分布律为
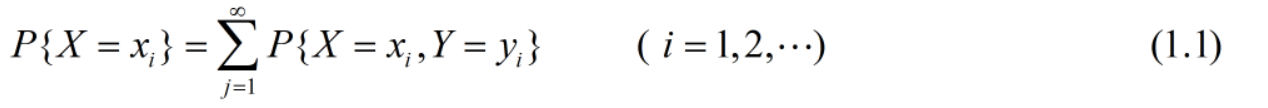
● Y的边缘分布律为
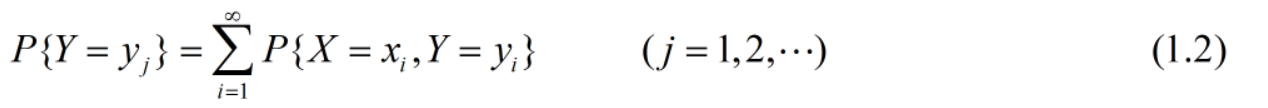
2、若已知(X, Y)的联合分布律和X的边缘分布律 => 可以求出Y的条件分布律
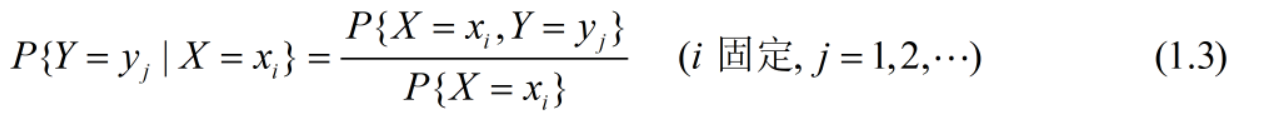
3、若已知X的边缘分布律和Y的条件分布律 => 可以求出(X, Y)的联合分布律

4、若已知X的边缘分布率和Y的边缘分布率 => 只有当X和Y相互独立时,才可以求出(X, Y)的联合分布率
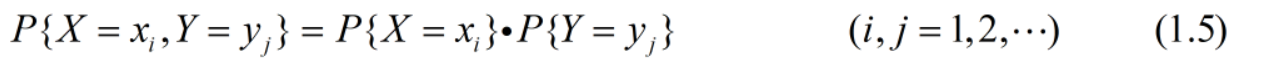
✔ 综合应用:若已知X的边缘分布率和Y的条件分布律,如何求X的条件分布律?
求解分析:只需综合运用上述的几种情况即可,思路如下图所示:

求解过程如下图所示,可以看出,我们始终是根据条件分布律的定义,对分子上的(X, Y)联合分布律和分母上的Y边缘分布律进行变形处理,将等式转化为题目已知的X边缘分布律和Y条件分布律进行表示。

二、问题的引入
例:某矿山一年内发生的事故总数服从泊松分布X ~ P(λ),其中一个事故是致命的概率为 p (0 < p < 1),事故发生之间相互独立。设一年内发生发生致命事故的次数为Y,求Y的分布律。
三、问题的分析
分析:该问题含有两个随机变量:事故总数X和致命事故总数Y。题目所要求的Y的分布律实质上为该二维随机变量的边缘分布律。显然致命事故发生的次数Y与事故总数X之间必然有着某种联系,根据题目给出的其中一个事故是致命的概率为 p,可以求出Y在X = k(k为事故发生的次数)下的条件分布律,注意这里Y的条件分布律服从二项分布,即

由于矿山事故为稀有事件,所以事故总数X服从泊松分布(这与题目所给条件相符),利用泊松分布的公式可以直接得到随机变量X的边缘分布率如下式所示:

求解思路:有了X的边缘分布律和Y的条件分布律,通过式(1.4)我们就可以得到(X, Y)的联合分布律,根据联合分布律由式(1.2)可以进一步求出Y的边缘分布率,求解过程如下图所示:

四、问题的求解
根据X的边缘分布律和Y的条件分布律,通过乘法公式(式1.4)计算出二维随机变量(X, Y)的联合分布律。(注意致命事故发生的次数m一定小于或者等于事故发生的次数k)

根据联合分布律,遍历完X的所有可能取值,就可以得到Y的边缘分布律。当求P(Y = m)时,注意到隐含的条件是:事故发生的次数k只可能大于或者等于m,即k ≥ m。所以我们只需在Y = m的情况下,将k = m到k = ∞之间的所有联合分布律求和,即可得到P(Y = m)。

结果表明,致命事故发生的次数Y服从泊松分布,这与我们的预想的确是一致的,因为致命事故的发生是比单纯发生矿山事故更稀有的事件,所以自然也服从泊松分布,而泊松分布的均值恰好为λp(矿山事故发生的均值 * 事故发生后致命的概率)。