题目

本题链接：求最小公倍数

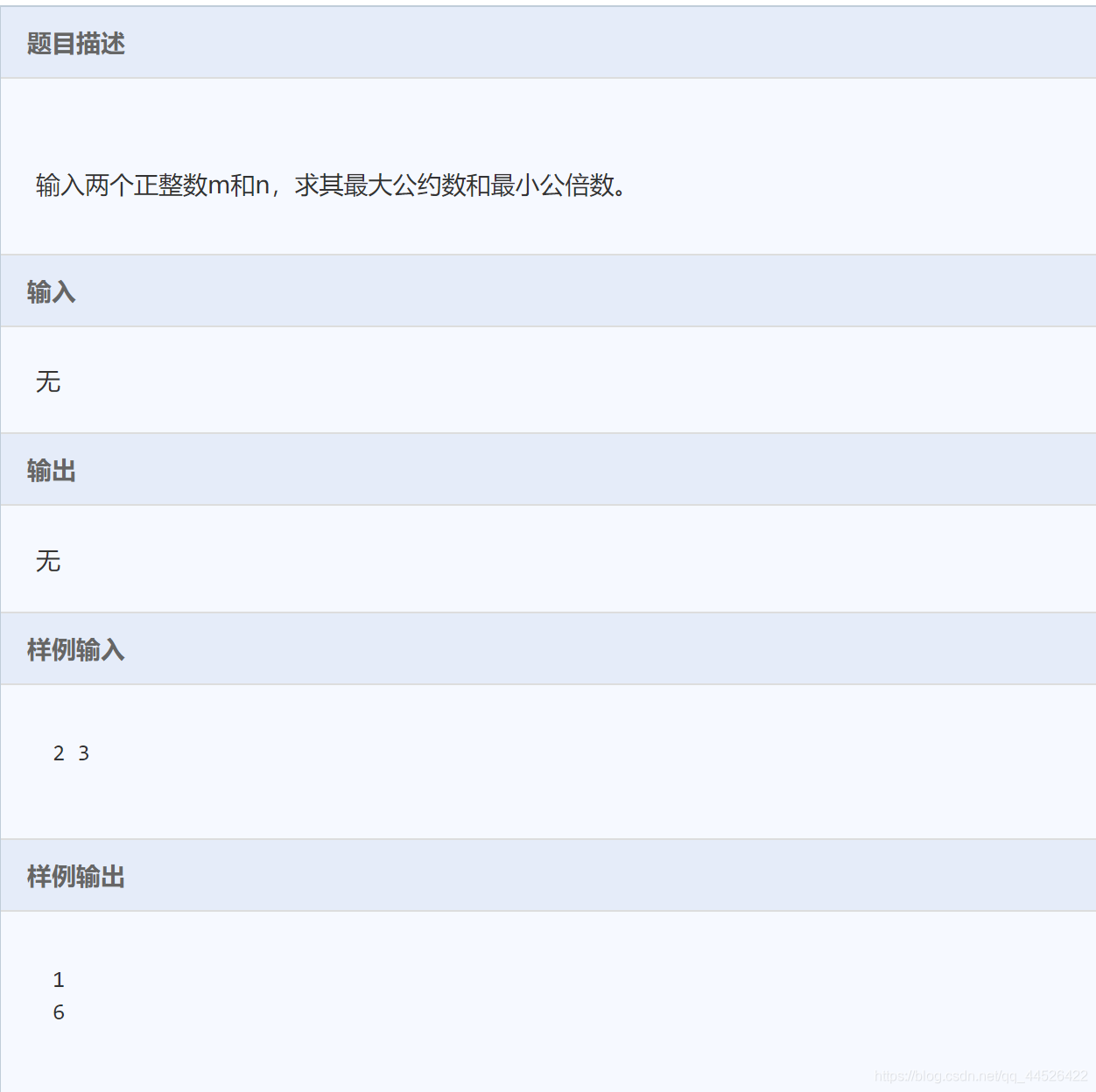
正整数A和正整数B 的最小公倍数是指能被A和B整除的最小的正整数值，设计一个算法，求输入A和B的最小公倍数。

输入描述：

输出描述：

示例1：

解题思路一： 暴力破解

从两个数中较大的数开始，逐个进行判断，能够被两个数整除，则第一个就是最小公倍数。

代码：

#include<iostream>
using namespace std;int main()
{int a, b;while(cin >> a >> b){int m = max(a, b);//a,b中的较大值while(1){if(m % a == 0 && m % b == 0){cout << m <<endl;break;}m++;//从较大的数开始,一个数一个数往后判断}}return 0;
}

暴力求解的效率太低，需要另一种方法来求解问题。

解题思路二： 更优方法

最小公倍数 = 两数之积除以最大公约数，在这里使用辗转相除的方法求解最大公约数，即a与b的最大公约数可以转化为a、b之间的余数为两者之间最小的数之间的公约数。所以对于输入的两个数进行连续求余，直到余数为0，求余的分母即为结果。

辗转相除法求最大公约数举例：25 15求最大公约数
25 % 15 = 10，10不等于0，继续取余
15 % 10 = 5，5 等于0，继续取余
10 % 5 = 0，所以求得最大公约数5

代码：

#include<iostream>
using namespace std;//求最大公约数
int gcb(int a, int b)
{int c = 0;while(c = a % b){a = b;b = c;}return b;
}int main()
{int a, b;while(cin >> a >> b){//最小公倍数 = 两数之积除以最大公约数cout << a * b / gcb(a, b) << endl;}return 0;
}