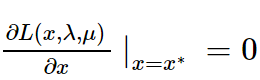分区式管理是满足多道程序的最简单的存储管理方案。它的基本思想是将内存划分成若干个连续区域，称为分区。每个分区只能存储一个程序，且程序也只能在它所驻留的分区中运行。

⑴固定分区

操作系统预先把可分配的主存空间分割成若干个连续区域，如下图：

一旦分好，则每个分区的大小固定不再变化，且分区的个数也不再改变。一个分区只能容纳一道作业。
固定分区分配算法:(如右图)

①固定分区回收算法

只需将分区说明表中相应的分区的占有标志位置成“0”即可。

②固定分区的优缺点

内存分配、回收算法简单，容易实现。（优点）
主存空间利用率不高，容易造成内零头。（缺点）

⑵可变分区

动态地划分内存。即在作业在装入内存时把可用内存“切出”一个连续的区域分配给该作业，且分区大小正好适合作业的需要。为了实现动态分配，系统设立空闲分区链表：

每个空闲块的前后两个单元，放置必要的说明信息和指针。系统只要设立一个链首指针，指向第一个空闲块即可。分配程序可以依照自由块链表，来查找适合的空闲块进行分配。（如下图）

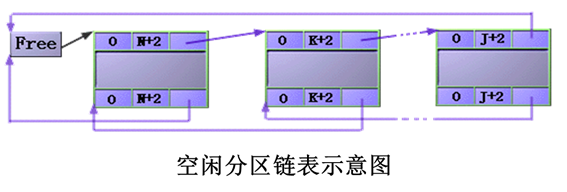
①可变分区分配算法

按空闲块链接的方式不同，可以有以下四种算法：
(a)最佳适应法 为作业选择分区时总是寻找其大小最接近于作业所要求的存储区域。
最佳适应算法：（best fit algorithm）。“最佳”的含义是指每次为作业分配主存时 ，总是把既能满足要求，又是最小的空闲区分配给作业，以免由于“大材小用”而浪费主存。为了加速查找，该算法要求将所有的空闲区按其大小递增次序排列。
设作业序列： A：12K B：3K C：10K

(b)最坏适应法
与最佳适应法相反，它在作业选择存储块时，总是寻找最大的空白区。
作业序列： A：12K B：3K C：10K

©首次适应法
为作业选择分区时总是按地址从低到高搜索，只要找到可以容纳该作业的空白块，就把该空白块分配给该作业。
首次适应算法：（first fit algorithm）。在该算法中，把主存中所有空闲区按其物理地址递增的次序排列。在为作业分配存储空间时，从低址空闲区开始查找，直到找到第一个能满足要求的空闲区后，从中划出与请求的大小相等的存储空间分配给作业，余下的空闲区仍留在空闲区表或链中。
作业序列： A：12K B：10K C：3K

(d)下次适应法
类似首次适应法，每次分区时，总是从上次查找结束的地方开始，只要找到一个足够大的空白区，就把它划分后分配出去。
下次适应算法：（next fit algorithm）。该算法是首次适应算法的变形，在为作业分配存储空间时，是从上次所分配的空闲区的下一个空闲区开始查找，直到找到第一个能满足要求的空闲区，从中划出一块与请求的大小相等的一块存储区分配给作业。在该算法中应采取循环查找方式，即最后上个空闲区的大小仍不能满足要求时，应再从第一个空闲区开始查找，故又称为循环造就算法。
作业序列： A：12K B：10K C：3K

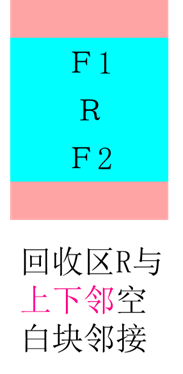
⑵可变分区回收情况

设R：回收区； F1：上邻空白块；
F2：下邻空白块

⑶可重定位分区

紧凑技术
为了消除外零头，进一步提高主存的利用率，定时地（或者在主存空间紧张时）把主存中的作业“搬家”集中在主存的一端。另一端就产生了一个大的空闲区。这种技术称为存储器的“紧凑 ”。

可重定位分区的优缺点
解决了可变分区分配所引入的“外零头”问题。（优点）
消除内存碎片，提高内存利用率。（优点）
提高硬件成本，紧凑时花费CPU时间。（缺点）

⑷多重分区

以上讨论都是基于一个作业在主存中占据的是一个连续分区的假定。为了支持结构化程序设计，操作系统往往把一道作业分成若干片段（如子程序、主程序、数据组等）。这样片段之间就不需要连续了。只要增加一些重定位寄存器，就可以有效地控制一道作业片段之间的调用。
如下图所示，作业Ａ、Ｂ分别被分成两个片段放进互不相连的存储区域中。由两个变址寄存器实现控制。

⑸分区的保护

为了防止一道作业有意或无意地破坏操作系统或其它作业。一般说来，没有硬件支持， 实现有效的存储保护是困难的。通常采取：界限寄存器方式 和保护键方式 两种措施，或二者兼而有之。

①界限寄存器方式

②保护键方式

注意：保护键0是指定分配给操作系统使用的。

欢迎大家加我微信交流讨论（请备注csdn上添加）