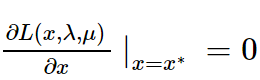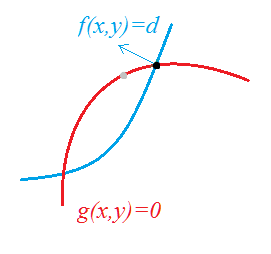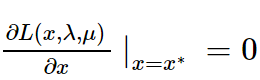为什么出现拉格朗日乘子法？

• 最短路径问题
• 从几何意义中获得灵感：
• 从数学公式中获得灵感
• 推广到高维空间

一个最短路径问题

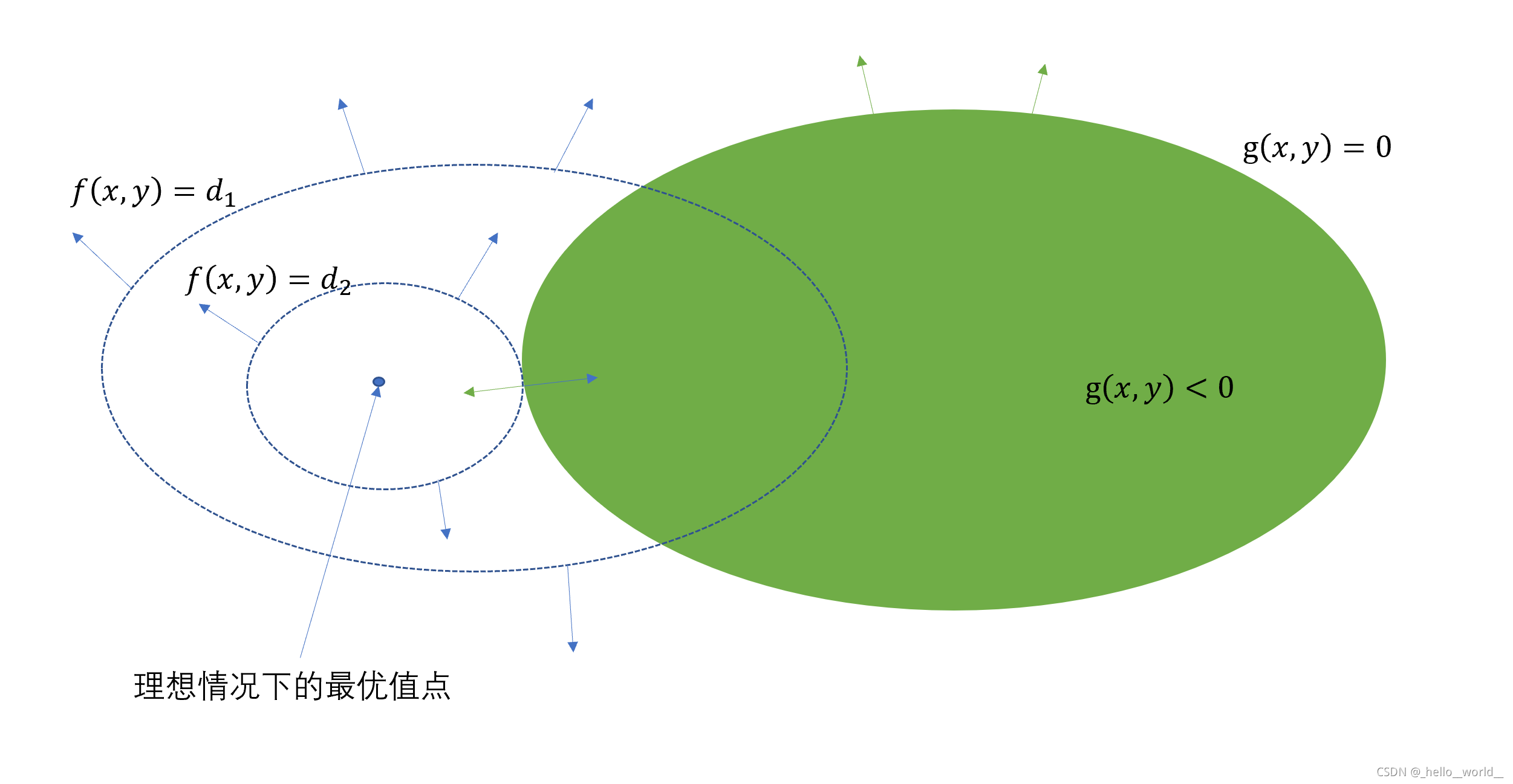
假设你在M点，需要先到河边（上图右侧曲线 ）再回到C点，如何规划路线最短？

 

假设：
河流曲线满足方程 g(x,y) = 0 （例如 如果它是一个圆：)

用P表示河边上的任意P(x,y)点，
用d(M,P)表示M,P之间距离，
那么问题可以描述为：,约束;

如何求解问题？

1. 从几何意义中获得灵感：

首先，f(P)是一个标量（只有大小没有方向），那么在上图的二维空间中必然存在了一个标量场f(P)，即对于每一个点P都对应着一个f(P)值，它代表经过该点的路径总和是多少。
如果我们画出它的等值线（场线)，就会发现它呈椭圆向外辐射：

显然，f(P)的等值线与河边曲线的交点P即为我们想求的点。

 

那么问题来了: 这样的点满足何种性质？ （如果没有性质也就无法列出关系式进行求解，但是这么特殊的点极有可能存在良好某种特性）

 

最直观的性质： 等值线（椭圆）在P点的法向量n与河边曲线的法向量m平行：

而在多元微积分中，一个函数h在某一点P的梯度是点P所在等值线（二维）或等值面（三维）的法向量，即,所以对于f,g

即：

即由相交点的性质我们得到了2个关系式（因为是二维平面，对于三维则可以得到三个关系式，以此类推），

再加上我们的约束条件：

一共3个关系式，由线性代数中知识可知 3个关系式，3个未知量()极有可能有唯一解，当然也不排除会出现多个解甚至无穷多解 （例如 下图 河边是一条直线，且M,C就在河边时）。

2. 从数学公式中获得灵感

仍人是问题：

3. 推广到高维空间
以上我们一直在讨论 二维的情形，下面让我们看看这个问题的高维情况： 以几何观点为例：

假设约束条件变成

学习总结：

若函数 f(x,y,z) 的变量受约束 g(x,y,z)=0限制, 函数的极值可以用下面Lagrange乘子法求出.

 

 

参考地址：https://www.zhihu.com/question/38586401

http://www.slimy.com/~steuard/teaching/tutorials/Lagrange.html