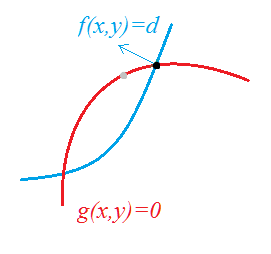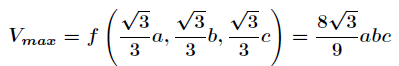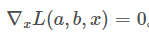昨天有位朋友让我看了一道题（见下图），方法是使用拉格朗日乘数法进行求解的，我刚开始算的时候感到非常困难，后来在答案的帮助下发现可以从x,y,z的对称性以及成比例暗示中着手，经此一题，我不由发问：向我这样计算能力薄弱的孩子考试遇到这种题该怎么办呢？因此，我便搜索了一些拉格朗日乘数法的一些技巧，希望有所帮助。


希望有经验的大佬们也可以指点一二🙂

参考：拉格朗日乘数法求解有什么技巧吗？

• 技巧一：硬核做差法
  这个方法可以去除 $\lambda$，进而转变为不含 $\lambda$ 的式子，再与 $\phi (x,y)=0$ 配合从而解出 $x,y$.
  
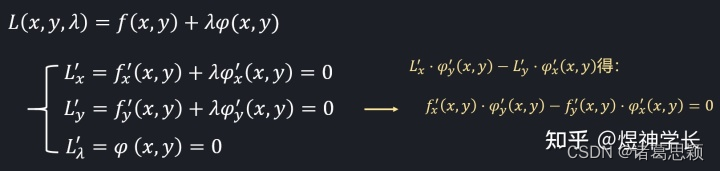
  对于三元函数类似，只不过这时候要作差两次
  

• 技巧二：单项连等法
  构造出相等的项，将其放在等号一边之后连等就可以了。该方法可以通过讨论消除 $\lambda$ ，进而变成不含 $\lambda$ 的连等式或直接得到 $\lambda =0$ 。
  

• 技巧三：对称作差法
  $f(x,y,z)$ 和 $\phi (x,y,z)$ 关于 $y=x$ 对称：我们需要做的是让 $L_x^{{}^{\prime }}=0$ 减去 $L_y^{{}^{\prime }}=0$，得到的式子可以变形成： $(y-x)(整式)=0$ ，从而简化计算。同时如果其中有 $y\ne x$ 的解，则将它的 $x$，$y$ 互换后则是另一个解。
  

• 技巧四：行列式求解法
  如果求出来的 $L_x^{{}^{\prime }}=0$, $L_y^{{}^{\prime }}=0$ , $L_z^{{}^{\prime }}=0$ 组成的为线性方程组，则可以根据线性代数知识解决
  
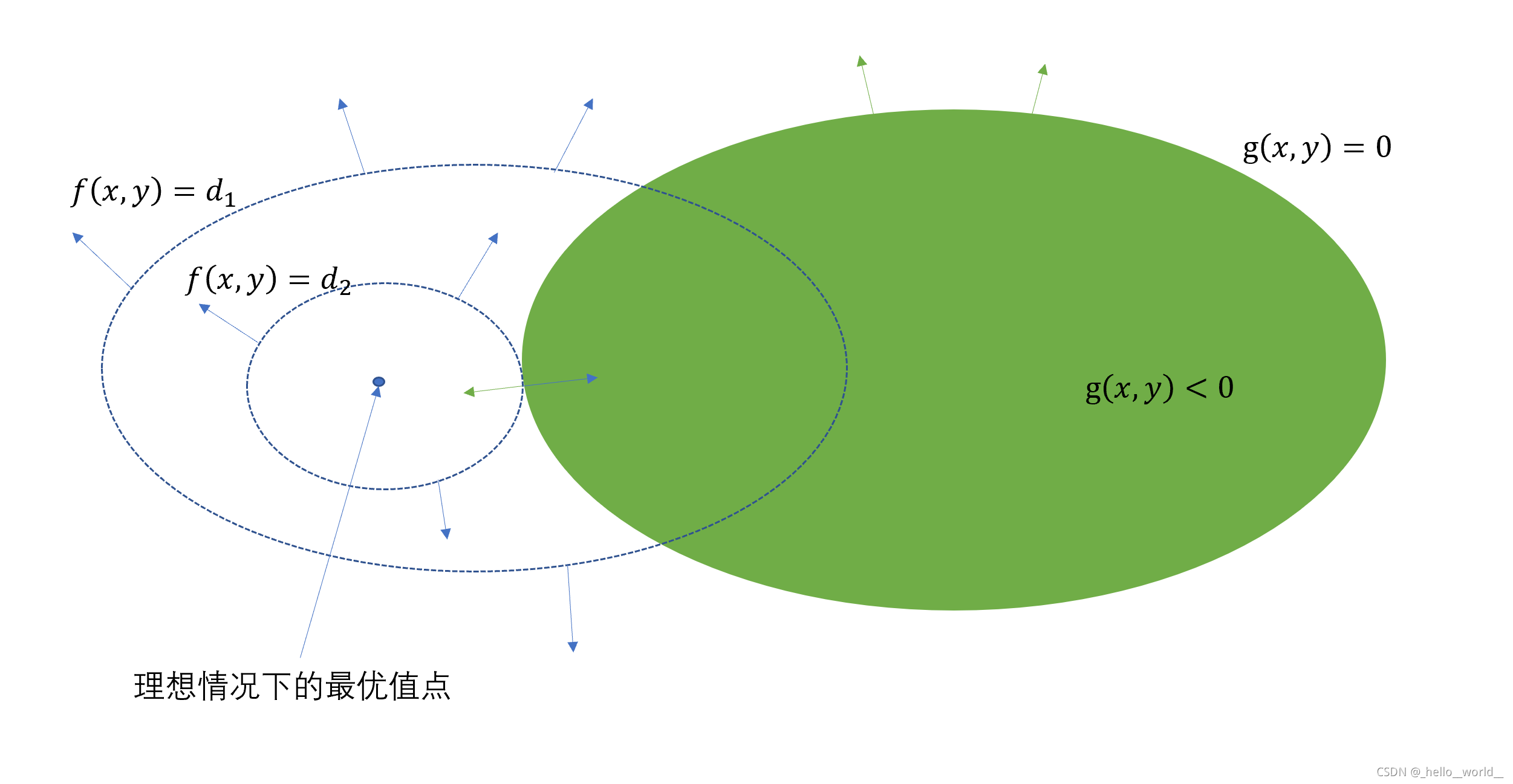
  这里由于 $x^2+y^2+z^2-10=0$的存在，将导致 $x,y,z$ 不可能同时为 0，因此 (1)~(3) 式所组成的线性方程组一定有非 0 解，因此就是系数行列式为 0，即可将 $\lambda$ 解出，减少未知数的个数，进而容易求解。

• 技巧五：齐次构造法
  这里我还不太明白，只知道将极值转化为 $\lambda$ 极值了，后期强化的时候再来看这个方法
  

• 技巧六：目标函数转换法
  这个我也不懂/(ㄒoㄒ)/~~
  
  注意：

• 技巧是死的，人是活的，在解题中要灵活的运用技巧。

• 解题时，有可能会出现增解的情况，平时解出极值点之后，建议再带点到每个方程中演算一下。这样也能检查自己的结果是否正确，是一个比较好的习惯。