我是一个有强迫症的人，什么文件都要归类，电脑桌面干干净净的放着几个必要的文件夹，所有的文件对应有不同的文件夹存放，如果看到某个文件（只要不是临时存放的）出现在桌面上，就感觉非常刺眼。
我就是这么管理电脑文件的，感觉…….没救了。

存储管理的功能
- 存储分配
- 存储共享
- 存储保护
- 存储扩充
- 地址映射
内存资源管理
- 内存分区
- 内存分配
  - 静态等长分区的分配
  - 动态异长分区的去配
- 紧凑
小结

存储管理的功能

存储管理可不仅是对外部存储资源（如磁盘文件）进行的管理，也包括了对内存的管理。内外存的资源管理技术可以相同，也可以不同，但一般情况下，都采用相同的管理技术。

存储管理主要是完成如下功能：存储分配，存储共享，存储保护，存储扩充，地址映射。

存储分配

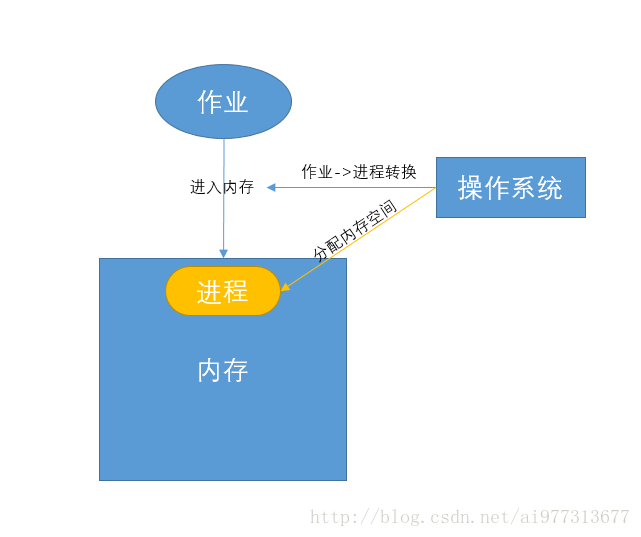
我们知道，当一个作业进入内存时，操作系统会将其转变为进程，同时为其分配存储空间以供运行，而进程运行结束时，操作系统将进程所占有的存储空间回收。

一般的存储分配

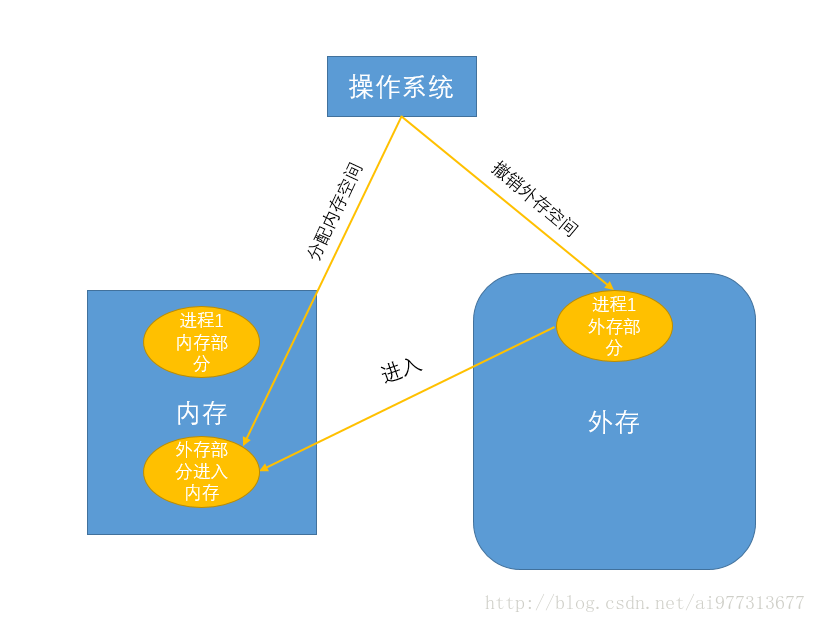
如果操作系统带有虚拟存储管理功能，那么进程运行过程中一部分存在于内存，另一部分存在于外存。如果外存部分进入内存，则撤销外存空间，分配内存空间，反之，操作相反。

带虚拟存储管理的内存分配

仅仅知道要这样分配还不够，操作系统得记录这些情况——内存与外存资源的使用情况，为此，操作系统设置了两个表用于记录这些信息：
1. 分配表：记录已经分配的区域。
2. 空闲表：记录未分配区域。

存储共享

多个进程共用内存中的相同区域。

经常去吃烧烤的小摊儿上就一个老板在忙活，不管谁的串都是老板烤的，但如果老板雇佣很多人，然后不同客人的串分给不同的人去烤，那老板多轻松啊（但这赚的估计还不够老板发工资）。
据说高档餐厅会为每个桌配一名侍者，不过我没去过就是了……

我们之所以要进行存储共享，其一便是为了节约内存空间，不然多个进程同时需要使用一个程序资源时，还要为每个进程创建一个程序资源的副本，那内存就算再大也不够用啊（就像那个烧烤摊儿老板，赚的还不够给工人发的工资）。
另一方面，使用存储共享也是为了方便进程通信，我们知道PV操作就需要公共的内存空间才能够实现。

一般情况下我们需要共享的是代码和数据，共享代码是为了节约内存空间，而数据则是对应的方便进程通信（也能节约内存空间）。

存储保护

存储共享中我们提到了PV操作，那PV操作是为了限制多个进程出现同时进入临界区的情况所提出来的，也算是一种对共享变量的一种保护，不过在存储保护中这种保护则更甚一筹，即对于多个进程共享的存储区域的保护。
存储保护主要包括以下两个方面：
1. 防止地址越界
这个比较容易理解，因为在我们写程序的时候也要注意的，一旦地址越界编译就会出错，无法通过，不过此时还能在编译失败时纠正。
而在操作系统中，每个进程具有相对独立的进程空间，一旦其中一个进程运行时产生的地址出现在其自身的进程空间之外，此时发生了地址越界，如果侵犯了其他进程空间，就会影响其他进程的正常执行，假如侵犯的进程空间属于操作系统，就可能导致系统崩溃。
2. 防止操作越权
对于多个进程共享的存储空间，每个进程有自己的访问权限，如读，写，执行。如果该进程访问共享区域时违反了权限规定，就说这个进程发生了操作越权。
一般我们选用硬件来提供存储保护，软件作为辅助。

我们用Windows的时候，如果在系统盘里删一些东西，会有提示说需要提供权限，这就是说当前登录用户权限不够，不能做这种操作。

存储扩充

我们知道，cache是高速缓冲，读写速度仅次于寄存器，但是耐不住人家尊贵，如果直接使用cache作为存储器的话，我只能说：“土豪，交个朋友吧！”。
当然了，这只是玩笑话，cache很贵，其次是内存很贵，再然后咱么所说的机械硬盘就是大街货了，便宜，容量都是以TB做单位的。
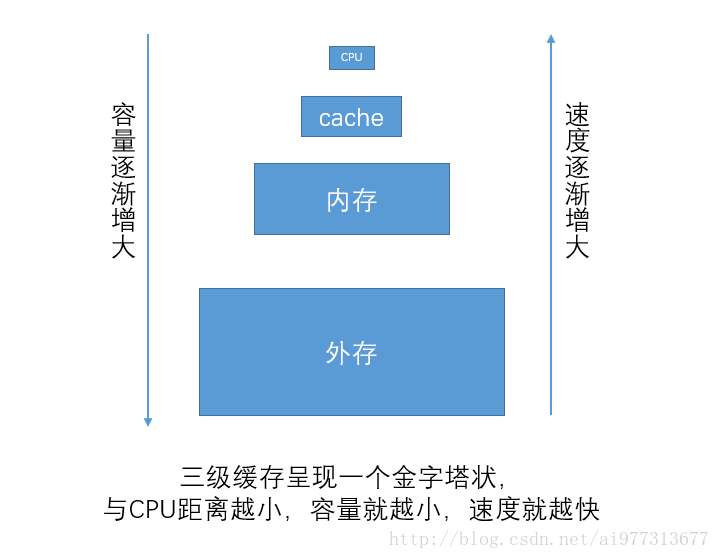
所以为了省钱，也为了性价比，我们就提出了三级缓存，将cache，内存，还有外存有机的结合，形成一个容量大速度快的虚拟存储系统。

三级缓存都是比较新的技术了，很多年前，还没有cache这个东西，只有内存和外存之说。

三级缓存

地址映射

逻辑地址转换成物理地址的过程。
完成地址映射的硬件机构称为存储管理部件（MMU）。

地址映射

逻辑地址是相对的，因此可以被映射到物理地址的不同的位置，物理地址则是绝对的，一旦产生，便固定了，这对于程序的结构化和分层设计带来不便。
之所以会使用逻辑地址，也是为了程序移植方便。

内存资源管理

内存分区

对内存分区，可以是静态，可以是动态的，分区的大小可以是等长，也可以是异常的。
所谓静态分区，则是在系统运行之前就将内存划分为若干区域，后期可以直接分配。

但是，由于分配时只能对已划分好的分区进行选择，故很难出现正好合适的区域。

动态分区与之对应，是在系统运行的过程中划分内存空间。

通常，按照进程所需存储空间的大小为其分配一个或多个区域。

等长和异长听名字就知道了，就不废话了。
一般情况下，我们都是使用静态等长和动态异长的组合方式。

内存分配

静态等长分区的分配

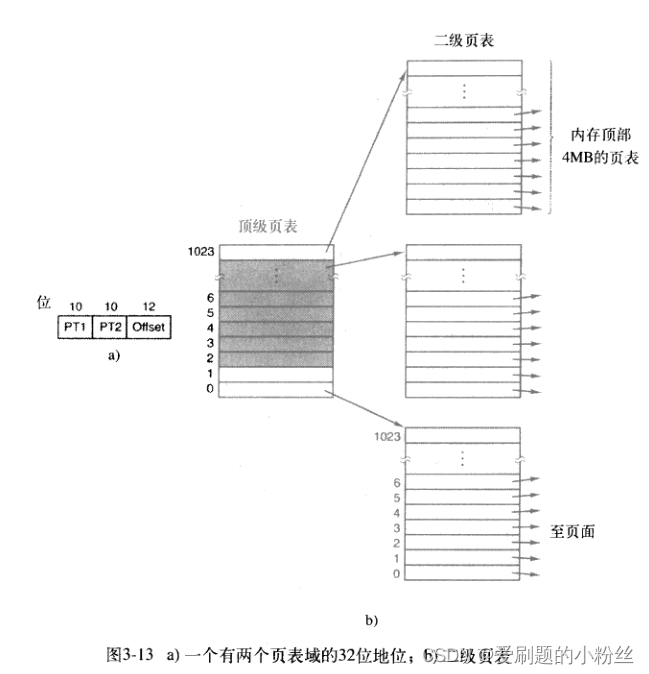
通常用于页式和段页式的存储管理方式，被静态的划分为等长区域，每个区域大小为2^iB，称之为页面。
分配与去配的表示方法：

位示图
用1位（1bit）来表示一个页面状态，1表示被占用，0表示空闲。假设某个存储空间内忧n个页面：
空闲页面表
若干个连续的空闲页面作为一组登记在空闲页面表中，该表包含首页面号与页面个数。这种分配方法能使一个进程的若干页面连续。

页面首号是指一块连续空闲区的第一块空闲页面号，页面个数则是这块连续空闲区的页面总数。
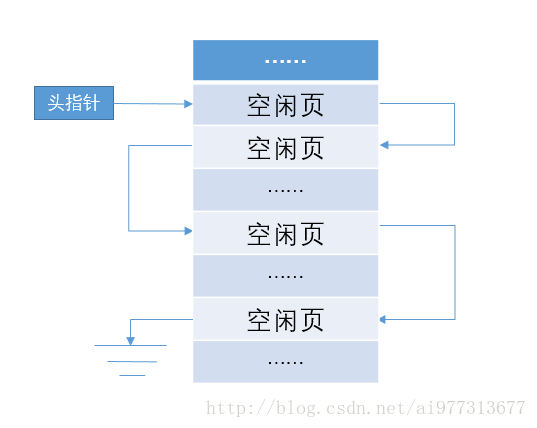
空闲页面链
所有的空闲页面连接成一个链表，分配时取链表头页面，去配（撤销）时将释放的页面连接到链表头。

这种方法适用于内存页面的分配，对于外存，由于需要数据的传输，故而速度慢，不采用。

动态异长分区的去配

此种分区常用语界地址和段式存储管理方式。
存储空间被划分为若干不等长区域，对此的管理采用空闲区域表，该表中记录所有当前未被进程占用的空闲区域。

与空闲区域表相关的算法：

最先适应算法（First Fit）
核心思想：对于存储申请命令，选取空闲区域表中满足申请长度，且起始地址最小的空闲区域。
实现：空闲区域表中的首址按从大到小的次序依次被记录了，当进程申请存储空间时，系统从该表的头部开始查找，取满足要求的第一个表目项，对比长度，若空闲区域大于进程申请空间，进行分割，然后将与申请空间大小相同的空闲区分配给进程，将剩余部分保留在空闲区域表中（需要改变首址）。

该算法尽可能的使用低地址，造成高地址空间形成较大空闲区，算是一个优点，但是对空闲区的分割又是一个缺点（假设某个空闲区本来刚好可以满足P1的空间申请，但是P2先提出了空间申请，致使空闲区被分割，如此P1的申请将无法被满足）。
下次适应算法（Next Fit）
核心思想：从上一次分配空闲区域的下一个位置开始，选取第一个可满足的空闲区域。
实现：用一个指针记录每次分配结束后的下一个位置。

此算法不需要像FF算法一样，每次分配都要进行一次查询，减小了时间开销，使空闲区域分布的较为均匀，但依旧没有解决FF算法的缺点。
最佳适应算法（Best Fit）
核心思想：分配时寻找满足空间申请并且长度是最小的空闲区域，这样就克服了FF算法的缺点。
实现：空闲区域按地址由小到大的记录，然后从表头开始查找，过程与FF算法类似，只是多出了一项长度的比较。

可以预见，BF算法克服了FF算法的缺点，不去分割大的空闲区，但是又可能会形成很小的无法使用的空闲区——碎片。
最坏适应算法（Worst Fit）
核心思想：分配时取满足空间申请，并且长度最大的空闲区域。
实现：按照空闲区域长度由大到小依次记录于空闲区域表中，进程申请空间时，取第一个满足要求的表目项。

克服了BF的缺点，却保留了FF算法的缺点。