存储管理
- 操作系统将外存的文件调入到内存中,以便CPU调用,如果调用的内容不在内存中,则会产生缺页中断;
- 产生缺页中断后,这事需要从外存调数据到内存中,然后CPU接着从断点继续调用内存中的数据;
- 在外存调入内存的过程中,是超大的文件,需要对超大文件的一些内容切割之后分散放置到内存中;
- 根据切割方式的不同,会有不同的存储和调用方式;
页式存储

- 分页存储管理就是页式存储的过程;
- 它会将文件和内存划分成相同大小的一些区域,这些区域称为:页或者块;
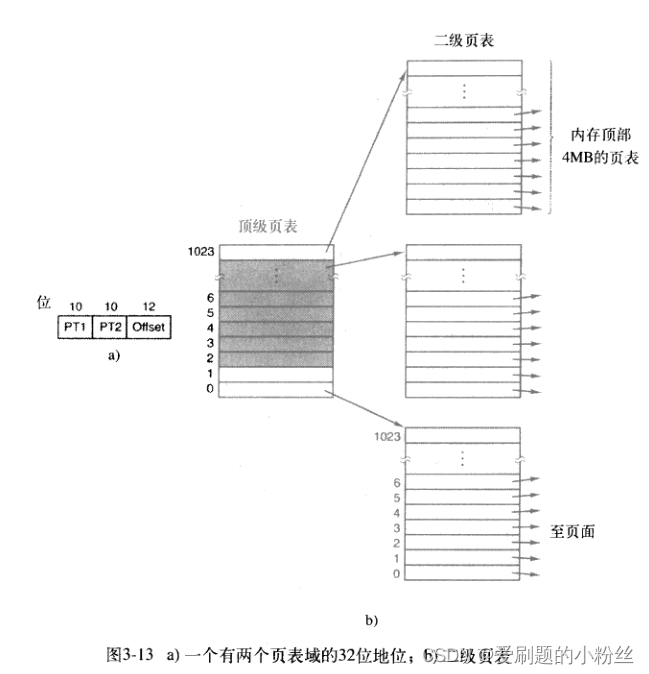
- 把用户程序和内存中文件之间的映射关系用一个表来记录,这个表就是页表;
- 页表中记录着用户程序中的页号,也叫做逻辑页号,用户程序的地址也叫做逻辑地址;
- 页表中记录着内存中文件切割后分散存放的块号,也叫做物理块号(页帧号),在内存中的地址也叫做物理地址;
- 根据用户程序中的逻辑地址查页表,从而得到内存中的物理地址;
- 逻辑地址和物理地址之间转换关系:
- 所有的地址划分成2个部分:页内的具体地址(页内地址,偏移量,相对位置),页外的页号编号(记录页内对应关系[记录在页表中](相对位置)的编号);
- 逻辑地址 = 页号 + 页内地址;
- 物理地址 = 百帧号(物理块号) + 页内地址;
- 页内地址保存不变,变化的只有页内的对应关系(逻辑地址中是页号、物理地址中是百帧号(物理块号));
- 完整的逻辑地址和物理地址可以用二进制、十六进制、十进制表示;
计算页内地址、页号、百帧号(物理块号)
- 涉及页面大小的定义;
- 页面大小转化为B,例如上图的4KB = 4096B = 2^12,那么页内地址的长度就是12位,上图中,二进制逻辑地址:10 1100 1101
1110,从低位到高位12位就是页内地址,此外就是页号10,10转换成十进制就是2,所以在页表中查询对应的百帧号就是6,十进制6转换为二进制110,页内地址保持不变,所以通过二进制逻辑地址:10
1100 1101 1110,和页内地址的长度12位,还有页表找到的物理地址就是:110 1100 1101 1110;
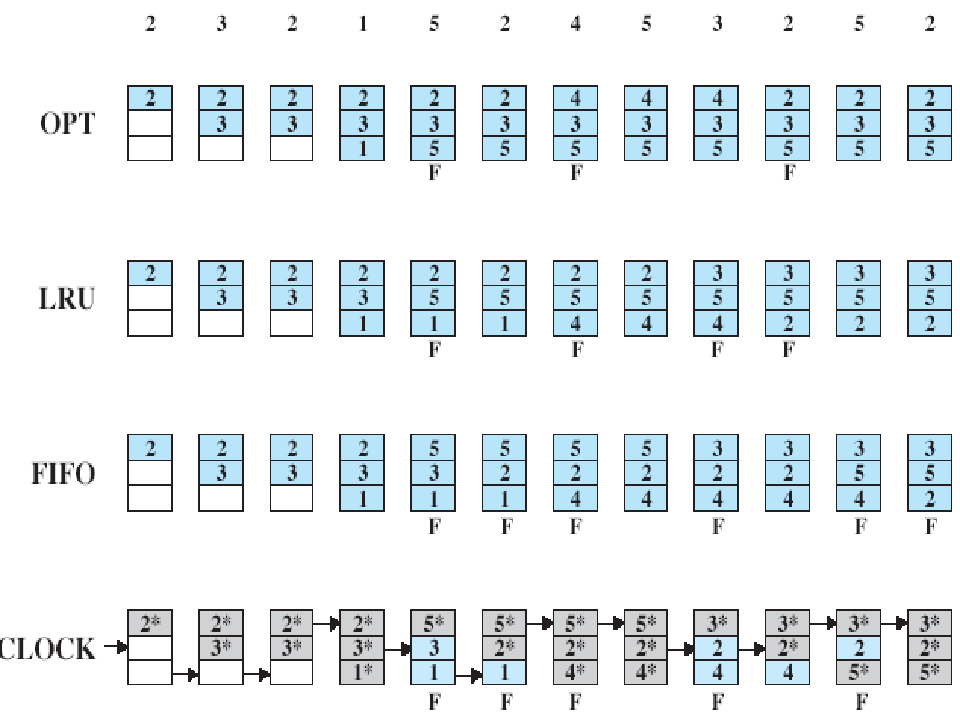
抖动现象
操作系统的抖动,又叫颠簸。颠簸是不作处理的计算机活动,通常是因为内存或其他资源耗尽或有限而无法完成所要执行的操作。当上述情况发生时,程序就会通过操作系统发出请求,操作系统就试图从其他程序中拿来所需的资源。

- 当内存不足时,需要淘汰其他在内存中进程的资源;
- 状态位记录进程是否在内存中,淘汰时无需考虑不在内存中的进程资源(不考虑状态位:0);
- 其次,访问位记录着是否最近被访问过,优先考虑最近访问过的,最近未访问的优先淘汰;
- 然后,修改位记录着内容最近是否被修改过,最近未修改过的先于修改过的被淘汰;
- 不考虑状态位:0 ----> 先淘汰访问位:0 ----> 再考虑淘汰修改位:0;
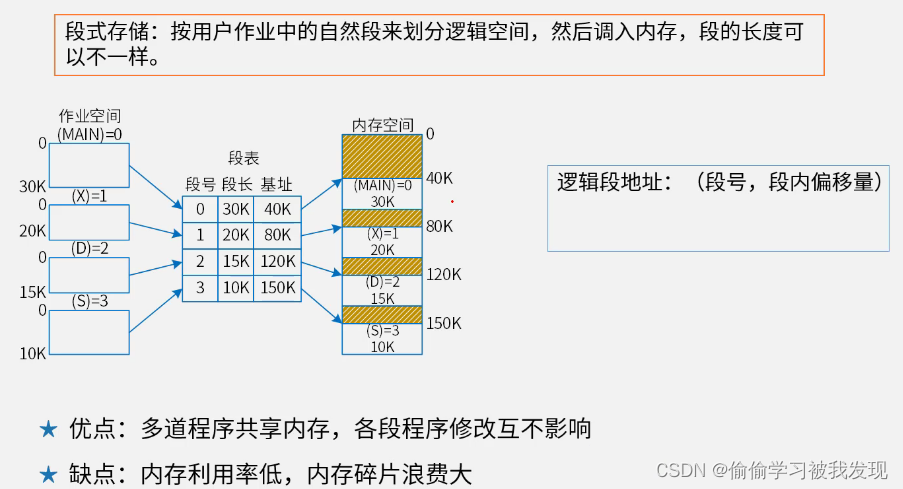
段式存储
- 页式存储从大小考虑文件在内存中,并没从需要切割的超大文件内容的逻辑连贯性去考虑划分;比如代码的连贯性;
- 从超大文件内容的逻辑连贯性去考虑划分,在内存中的存储,就有了段式存储;
- 按逻辑划分为不同大小的段,每段的起始位置就是段内偏移量;
- 段表中存有段号(每个自然段的开始位置),段长(每个自然段的大小不同,段的长度),基址(每段在内存中存储的开始位置);

- 逻辑地址:(段号,段内偏移量);
- 通过段号查段表得到基址,基址+偏移量就是在内存中的地址;
- 合法段地址就是要段号对应的内存地址中不溢出不能越界,该段的基址+偏移量没超过该段在内存存储的大小;
- 非法段地址:逻辑地址到物理地址转换时地址越界;
段页式存储
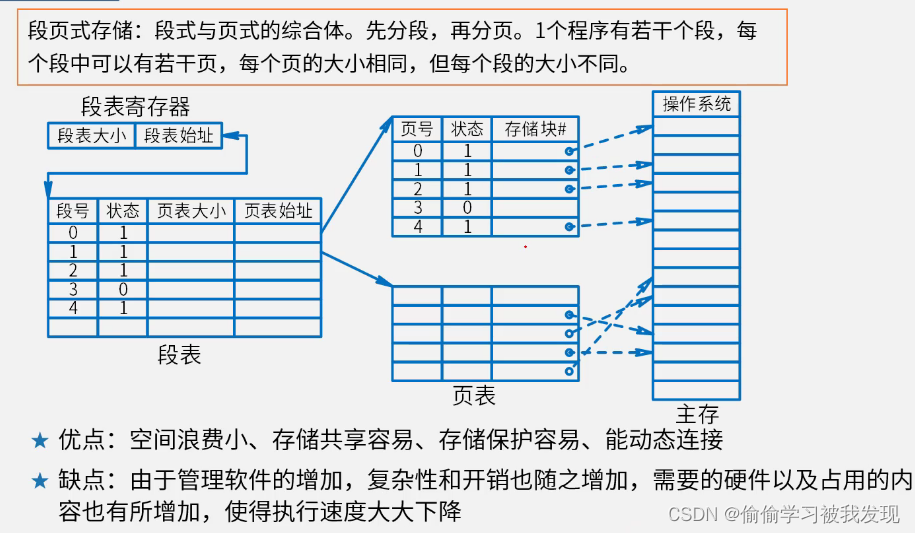
- 将段式存储管理和页式存储管理结合;

- 页内地址长度固定大小(上图有8-0+1的长度,所以有2^9个页内地址);
- 页号长度不固定(最多有:13-9+1的长度,所以有2^5个页号),大小不确定,大小不固定,可变长;
- 段号长度不固定(最多有:16-14+1的长度,所以有2^3个段号),大小不确定,大小不固定,可变长;