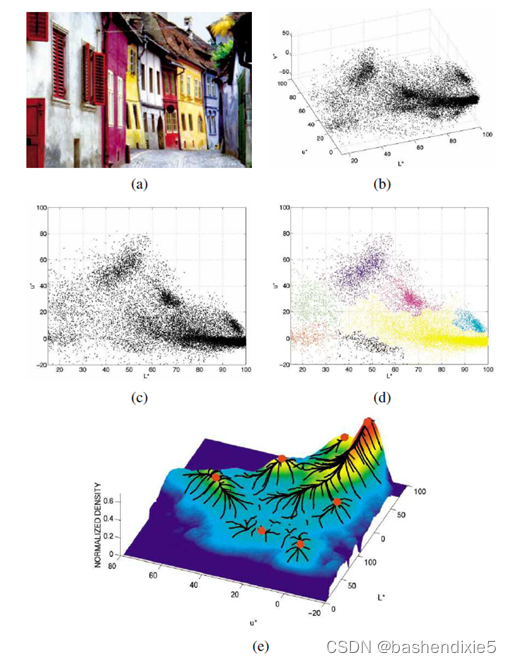
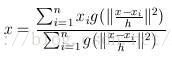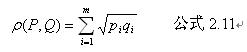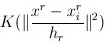Meanshift均值漂移聚类算法

article/2025/11/6 14:01:38

一、meanshift

均值漂移就是把指定的样本点沿着密度上升的方向移向高密度区域。这里可以用矢量加法的几何意义来理解。参考博文Mean Shift 聚类算法
meanshift为
M r ( x ) = 1 k ∑ x i ∈ S r ( x ) ( x i − x ) M_r(x)=\frac{1}{k}\sum\limits_{x_i\in S_r(x)}(x_i-x) Mr​(x)=k1​xi​∈Sr​(x)∑​(xi​−x)
其中 S r ( x ) = { y : ∥ y − x ∥ < = r } S_r(x)=\{y:\|y-x\|<=r\} Sr​(x)={y:∥y−x∥<=r}， k k k是 S r ( x ) S_r(x) Sr​(x)中点的个数。
更 新 x = x + M r ( x ) 更新x=x+M_r(x) 更新x=x+Mr​(x)
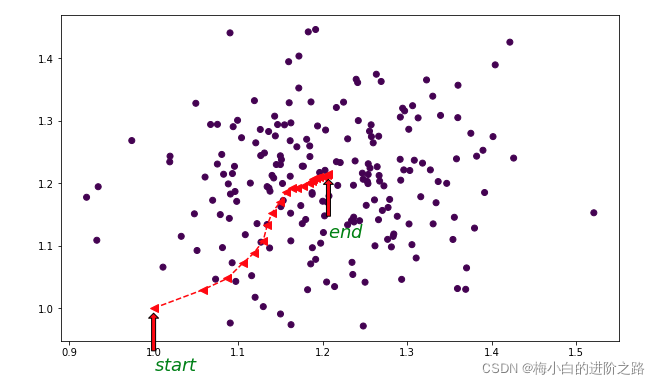
在这里插入图片描述
实现上图的python代码：

from sklearn.datasets import make_blobsX1,y1=make_blobs(n_samples=200, n_features=2, centers=[[1.2, 1.2]],cluster_std=[[.1]], random_state=9)
plt.scatter(X1[:,0],X1[:,1],c=y1)
def meanshift(point,X,r,eps):pointNeigh=X[np.linalg.norm(X-point,axis=1)<=r]shift=np.sum(pointNeigh-point,axis=0)/len(pointNeigh)points=[point]while np.linalg.norm(shift)>eps:point=point+shiftpointNeigh=X[np.linalg.norm(X-point,axis=1)<=r]shift=np.sum(pointNeigh-point,axis=0)/len(pointNeigh)points.append(point)return pointspoints=meanshift(np.array([1,1]),X1,0.1,0.000001)
points=np.array(points)
plt.figure(figsize=(10,6))
plt.scatter(X1[:,0],X1[:,1],c=y1)
plt.plot(points[:,0],points[:,1],'r<--',markersize=8)
plt.annotate(r'$start$', xy = (1, 1), xytext = (1, 0.9),arrowprops = {'headwidth': 10, # 箭头头部的宽度'headlength': 5, # 箭头头部的长度'width': 4, # 箭头尾部的宽度'facecolor': 'r', # 箭头的颜色'shrink': 0.1, # 从箭尾到标注文本内容开始两端空隙长度},family='Times New Roman',  # 标注文本字体为Times New Romanfontsize=18,  # 文本大小为18fontweight='bold',  # 文本为粗体color='green',  # 文本颜色为红色# ha = 'center' # 水平居中
)
plt.annotate(r'$end$', xy = (points[-1][0],points[-1][1] ), xytext = (points[-1][0], points[-1][1]-0.1),arrowprops = {'headwidth': 10, # 箭头头部的宽度'headlength': 5, # 箭头头部的长度'width': 4, # 箭头尾部的宽度'facecolor': 'r', # 箭头的颜色'shrink': 0.1, # 从箭尾到标注文本内容开始两端空隙长度},family='Times New Roman',  # 标注文本字体为Times New Romanfontsize=18,  # 文本大小为18fontweight='bold',  # 文本为粗体color='green',  # 文本颜色为红色# ha = 'center' # 水平居中)

二、meanshift聚类

1.算法流程

需要给定的参数
bandwidth----带宽
Mindist—漂移均值收敛的阈值
center_distance----合并簇的阈值

第一阶段—聚类

需要初始化的集合
创建一个空的中心点集centers，用于存放各个簇所对应的中心点
创建一个空的集合results,用于存放各个簇所包含的点
1.将数据集X的点都标记为未访问unvisited；
2.从数据集X中取出一个点，记为point，判断它是否属于unvisited，如果属于，将其从unvisited删除，并进行第3步，否则重新从X取点；
3.创建一个空的集合result_point，用来存放point对应的簇中所包含的点；
4.从X中找到位于以point为中心，带宽为bandwidth之内的点，用neighbor表示；
5.判断neighbor是否为空集，则返回第2步，否则将neighbor中全部点加入到result_point中，并将这些点从unvisited中删除；
6.计算point在neighbor上的漂移均值meanshift;
7.判断shift是否大于给定的阈值Min-dist，如果大于，更新点point=point+shift并返回第4步，否则将point加入到centers,result_point加入到results中，再返回第2步//

第二阶段–合并

由第一阶段得到centers和相应的results。由于centers中有一些中心点之间的距离可能很小，我们需要将其所对应的簇合并成一个簇，并更新中心点。

第三阶段–分组

由于X中的点可能位于多个簇（result_point）中，我们需要确定其到底属于哪一个簇。
统计每个点在各个簇中所出现点次数，次数最高的簇就是该点最终所属的簇。

2.python代码

import math
def euclidean_dist(self,pointA,pointB):""""""if pointA.shape==pointB.shape:##pointA和pointB是两个点return np.linalg.norm(pointA-pointB)else:##pointA和pointB中有一个是点集return np.linalg.norm(pointA-pointB,axis=1)def gaussian_kernel(dist,bandwidth):"""dist---欧式距离bandwidth---带宽"""weight=(1/(np.sqrt(2*math.pi)*bandwidth))*np.exp(-(dist**2)/(2*np.power(bandwidth,2)))return weight
def compute_shift(pointNeigh,point,bandwidth,kernel):if kernel==False:shift=np.sum(pointNeigh-point,axis=0)/len(pointNeigh)else:dists=np.linalg.norm(pointNeigh-point,axis=1)point_weight=gaussian_kernel(dists,bandwidth)point_weight=point_weight.reshape(len(point_weight),1)shift=np.sum((pointNeigh-point)*point_weight,axis=0)/np.sum(point_weight) return shiftdef Clustering(X,bandwidth,MinDist,kernel=False):"""init_result---各个簇所包含的点的索引,init_centers--中心点"""unvisited=list(np.arange(len(X))) #未访问点的索引init_result=[]  #用于存放结果init_centers=[]for i in range(len(X)):point=X[i]if i in unvisited:unvisited.remove(i) #删除以访问点c_i=[]indexs=np.where(np.linalg.norm(X-point,axis=1)<=bandwidth)[0]pointNeigh=X[indexs]   #点point点bandwidth内搭点c_i.extend(indexs)  #把这些点加入point为中心点簇中for j  in list(indexs):if j in unvisited:unvisited.remove(j)shift=compute_shift(pointNeigh,point,bandwidth,kernel)while np.linalg.norm(shift)>MinDist: #判断shift的大小point=point+shiftindexs=np.where(np.linalg.norm(X-point,axis=1)<=bandwidth)[0]if len(indexs)==0:breakpointNeigh=X[indexs]c_i.extend(indexs)for k  in list(indexs):if k in unvisited:unvisited.remove(k)shift=compute_shift(pointNeigh,point,bandwidth,kernel)init_centers.append(point)init_result.append(c_i)return init_result,init_centersdef merge(init_centers,init_result,center_distance):final_centers=[init_centers[0]]final_result=[init_result[0]]k=len(init_centers)i=1stats=Truewhile i<k:for j in range(len(final_centers)):if np.linalg.norm(init_centers[i]-final_centers[j])<=center_distance:final_centers[j]=(init_centers[i]+final_centers[j])/2final_result[j].extend(init_result[i])stats=Falsebreakif stats==True:final_centers.append(init_centers[i])final_result.append(init_result[i])i+=1stats=Truereturn final_result,final_centers   def groupPoint(X,final_result,final_centers):result_table=pd.DataFrame(np.zeros((len(X),len(final_centers))),index=range(len(X)),columns=range(len(final_centers)))for i in range(len(final_centers)):clusterI_index=final_result[i]for j in range(len(clusterI_index)):result_table.iloc[clusterI_index[j],i]+=1result_id=np.argmax(result_table.values,axis=1)   return result_id
def plot(X,result_id,final_centers):for i in range(len(final_centers)):plt.scatter(X[result_id==i][:,0],X[result_id==i][:,1])

三、测试

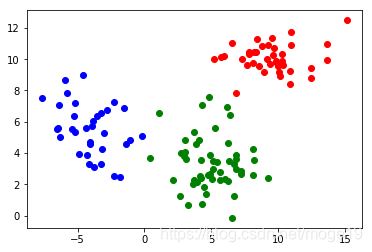
1.数据集一

from sklearn.datasets import make_blobs
X,y=make_blobs(n_samples=400, n_features=2, centers=[[1.2, 1.2],[-1,-1]],cluster_std=[0.2,0.3], random_state=9)
plt.scatter(X[:,0],X[:,1])

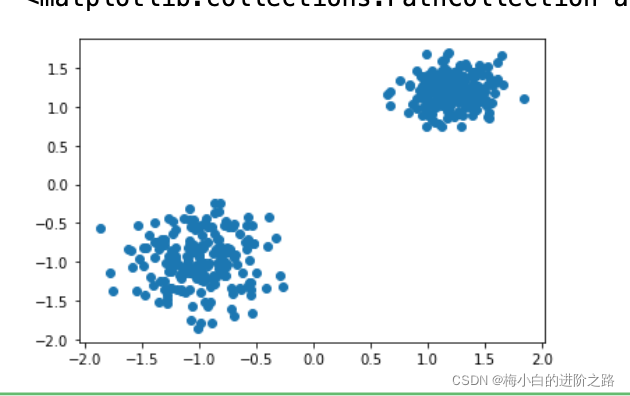
在这里插入图片描述

init_result,init_centers=Clustering(X,0.4,0.00001,kernel=True)
final_result,final_centers=merge(init_centers,init_result,1.2)
result_id=groupPoint(X,final_result,final_centers)
plot(X,result_id,final_centers)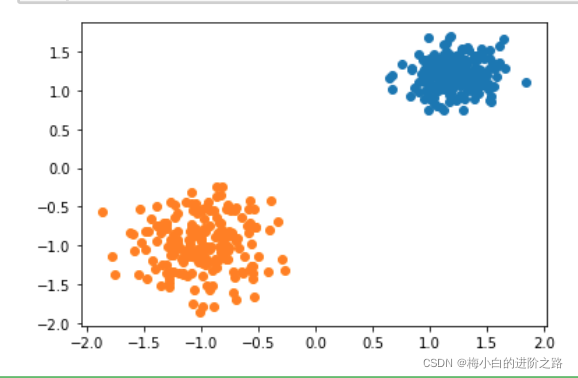

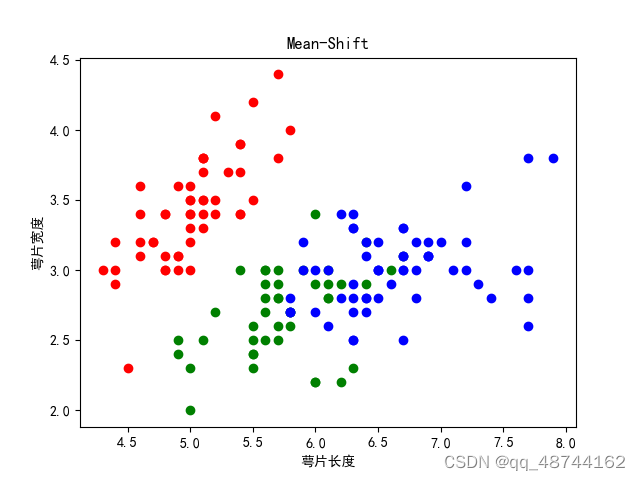
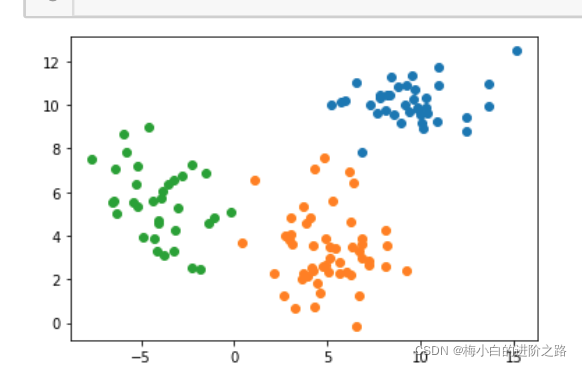
在这里插入图片描述

2.数据集二

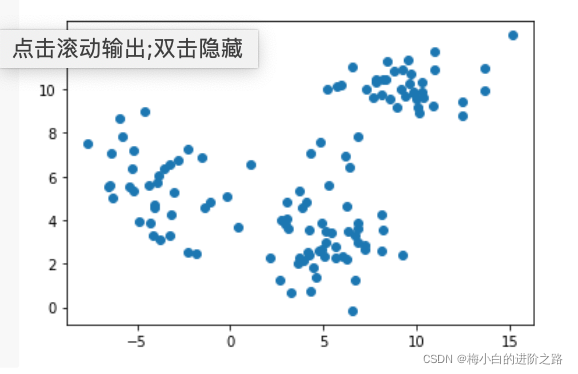
在这里插入图片描述

X_d=np.array(data)
init_result,init_centers=Clustering(X_d,4,0.00001,kernel=True)
final_result,final_centers=merge(init_centers,init_result,1.2)
result_id=groupPoint(X_d,final_result,final_centers)
plot(X_d,result_id,final_centers)

在这里插入图片描述

3. 数据集三


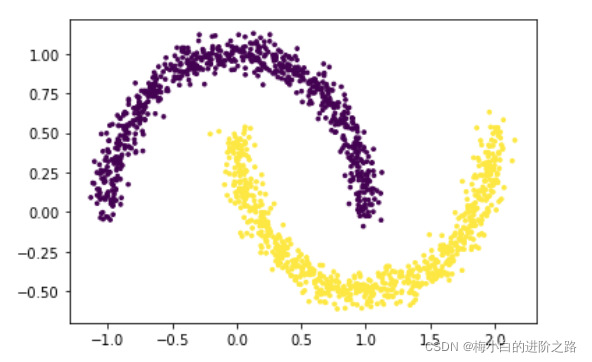
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons x,y = make_moons(n_samples=1500, shuffle=True,noise=0.06, random_state=None)
plt.scatter(x[:,0], x[:,1], c=y, s=7)
plt.show()

在这里插入图片描述

init_result,init_centers=Clustering(x,0.5,0.00001,kernel=True)
final_result,final_centers=merge(init_centers,init_result,1.)
result_id=groupPoint(x,final_result,final_centers)
plot(x,result_id,final_centers)

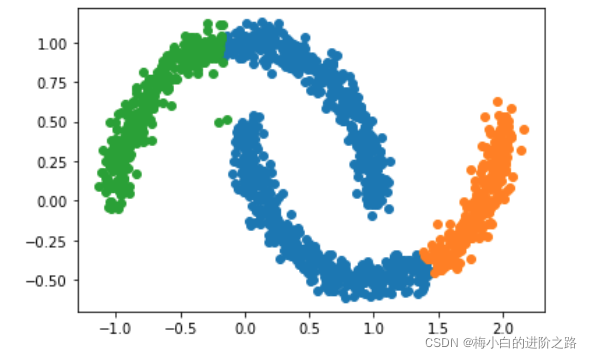
在这里插入图片描述
经过反复的调center_distance这个参数，都没有达到理想的聚类结果。

三、带有核函数的meanshift聚类

带有核函数的meanshift
m ( x ) = ∑ s ∈ S g ( ∥ s − x h ∥ 2 ) ( s − x ) ∑ s ∈ S g ( ∥ s − x h ∥ 2 ) m(x)=\frac{\sum\limits_{s\in S}g(\|\frac{s-x}{h}\|^2)(s-x)}{\sum\limits_{s\in S}g(\|\frac{s-x}{h}\|^2)} m(x)=s∈S∑​g(∥hs−x​∥2)s∈S∑​g(∥hs−x​∥2)(s−x)​
更新中心坐标：
x = m ( x ) + x x=m(x)+x x=m(x)+x

四、疑点

如何能把用于合并簇的阈值参数取消掉。


http://chatgpt.dhexx.cn/article/UWKbQggo.shtml

相关文章

MeanShift 目标跟踪

MeanShift 目标跟踪

MeanShift算法&#xff0c;又称为均值漂移算法&#xff0c;采用基于颜色特征的核密度估计&#xff0c;寻找局部最优&#xff0c;使得跟踪过程中对目标旋转&#xff0c;小范围遮挡不敏感。 文章目录 MeanShift 原理MeanShift 跟踪步骤meanShift 函数原型反向投影MeanShift 跟踪…
阅读更多...
MeanShift跟踪MATLAB实现

MeanShift跟踪MATLAB实现

一、简介 核跟踪方法是目标跟踪的主要方法, 应用非常广泛。例如Meashift、Camshift 算法, 它直接运用最速下降法的原理, 向梯度下降方向对目标模板逐步迭代, 直到迭代到最优位置。它的核心就是一步一步迭代寻找最优点, 在跟踪中, 就是为了寻找相似度值最大的候选区间。 本文主…
阅读更多...
OpenCV每日函数 对象追踪模块 Meanshift算法

OpenCV每日函数 对象追踪模块 Meanshift算法

1、meanshift的基本思想 meanshift 背后的直觉很简单。考虑你有一组点。（它可以是像直方图反投影这样的像素分布）。您有一个小窗口（可能是一个圆圈），您必须将该窗口移动到最大像素密度（或最大点数）的区域。如下图所示： 2、meanshift的原理简述 均值偏移和模式发现技术，…
阅读更多...
meanshift算法学习（二）：opencv中的meanshift

meanshift算法学习（二）：opencv中的meanshift

0.前言 接着上一篇文章点击打开链接说&#xff0c;opencv中提供的meanshift可以用来实现跟踪&#xff0c;其基本原理是迭代求解概率分布的“局部极值”。这一篇内容&#xff0c;我只讲opencv中的meanshift的用法和源代码分析。因为&#xff1a;&#xff08;1&#xff09;具体的…
阅读更多...
聚类算法之Mean Shift

聚类算法之Mean Shift

Mean Shift聚类算法 1. 基本原理 对于Mean Shift算法&#xff0c;是一个迭代得步骤&#xff0c;即每次迭代的时候&#xff0c;都是找到圆里面点的平均位置作为新的圆心位置。说的简单一点&#xff0c;使得圆心一直往数据密集度最大的方向移动。 2. 基本的Mean Shift向量形式…
阅读更多...
meanshift跟踪算法

meanshift跟踪算法

以下是用meanshift实现目标跟踪的实验报告&#xff08;包含源码&#xff09;&#xff0c;实验中详细介绍了meanshift跟踪算法的原理&#xff0c;结合OTB100跟踪数据集对meanshift跟踪效果进行了分析。 目 录 一.实验名称 二.实验目的 三.实验原理 3.1 前言 3.2 meanshift …
阅读更多...
传统目标跟踪——MeanShift算法

传统目标跟踪——MeanShift算法

目录 一、均值漂移&#xff08;MeanShift&#xff09; 二、流程 三、代码 3.1 meanshift&#xff0b;固定框的代码 3.2 优化&#xff1a;meanshift鼠标选择 3.3 meanshift自己实现函数 四、补充知识 4.1 直方图 4.2 归一化 4.3 直方图反投影 一、均值漂移&#xff08;…
阅读更多...
Mean Shift 聚类算法

Mean Shift 聚类算法

原文&#xff1a;https://blog.csdn.net/hjimce/article/details/45718593 一、mean shift 算法理论 Mean shift 算法是基于核密度估计的爬山算法&#xff0c;可用于聚类、图像分割、跟踪等&#xff0c;因为最近搞一个项目&#xff0c;涉及到这个算法的图像聚类实现&#xff…
阅读更多...
mean shift聚类matlab,机器学习：Mean Shift聚类算法

mean shift聚类matlab,机器学习：Mean Shift聚类算法

今天的文章介绍如何利用Mean Shift算法的基本形式对数据进行聚类操作。而有关Mean Shift算法加入核函数计算漂移向量部分的内容将不在本文讲述范围内。实际上除了聚类&#xff0c;Mean Shift算法还能用于计算机视觉等场合&#xff0c;有关该算法的理论知识请参考这篇文章。 Mea…
阅读更多...
Python 实现MeanShift算法

Python 实现MeanShift算法

原理 大家自行百度吧&#xff0c;我懒得码字了 推荐一下原理原理https://blog.csdn.net/jinshengtao/article/details/30258833 代码 直接上代码了&#xff0c;看不懂&#xff0c;就参照一下原理 # author: wdq # contact: 1920132572qq.com # datetime:2022/3/15 17:40 # …
阅读更多...
Sklearn聚类算法之meanshift

Sklearn聚类算法之meanshift

以二维来说明可能更容易理解&#xff0c;下图中的很多的红点就是我们的样本特征点&#xff0c;meanshift就是在这些点中的任意一个点为圆心&#xff0c;然后以半径R画一个圆&#xff08;在opencv中是一个矩形&#xff09;&#xff0c;然后落在这个圆中的所有点和圆心都会对应的…
阅读更多...
Python实现Mean Shift聚类算法

Python实现Mean Shift聚类算法

Mean Shift算法&#xff0c;又称均值聚类算法&#xff0c;聚类中心是通过在给定区域中的样本均值确定的&#xff0c;通过不断更新聚类中心&#xff0c;直到聚类中心不再改变为止&#xff0c;在聚类、图像平滑、分割和视频跟踪等方面有广泛的运用。 Mean Shift向量 对于给定的…
阅读更多...
mean shift 跟踪算法

mean shift 跟踪算法

说明一&#xff1a; Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其偏移均值,然后以此为新的起始点,继续移动,直到满足一定的条件结束. 1. Meanshift推导 给定d维空间Rd的n个样本点 ,i1,…,n,在空间中任选一点x&#xff0c;那么Mean Shift向量…
阅读更多...
Python实现Mean Shift算法

Python实现Mean Shift算法

声明&#xff1a;代码的运行环境为Python3。Python3与Python2在一些细节上会有所不同&#xff0c;希望广大读者注意。本博客以代码为主&#xff0c;代码中会有详细的注释。相关文章将会发布在我的个人博客专栏《Python从入门到深度学习》&#xff0c;欢迎大家关注~ 在K-Means算…
阅读更多...
meanshift算法 java_Meanshift，聚类算法

meanshift算法 java_Meanshift，聚类算法

记得刚读研究生的时候&#xff0c;学习的第一个算法就是meanshift算法&#xff0c;所以一直记忆犹新&#xff0c;今天和大家分享一下Meanshift算法&#xff0c;如有错误&#xff0c;请在线交流。 Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其…
阅读更多...
保边滤波之Mean shift filter

保边滤波之Mean shift filter

Mean shift filter 目录 Mean shift filter 一、算法原理 二、练手实现的算法代码如下&#xff1a; 三、实现结果 一、算法原理 在OpenCV中&#xff0c;meanshift filter函数为 pyrMeanShiftFiltering&#xff0c; 它的函数调用格式如下&#xff1a; C: void pyrMeanShif…
阅读更多...
mean shift

mean shift

参考&#xff1a; http://blog.csdn.net/google19890102/article/details/51030884 http://www.cvvision.cn/5778.html https://wenku.baidu.com/view/5862334827d3240c8447ef40.html http://blog.csdn.net/qq_23968185/article/details/51804574 https://www.cnblogs.com…
阅读更多...
机器学习算法原理与实践（二）、meanshift算法图解以及在图像聚类、目标跟踪中的应用

机器学习算法原理与实践（二）、meanshift算法图解以及在图像聚类、目标跟踪中的应用

【原创】Liu_LongPo 转载请注明出处 【CSDN】http://blog.csdn.net/llp1992 最近在关注跟踪这一块的算法&#xff0c;对于meanshift的了解也是来自论文和博客&#xff0c;本博客将对meanshift算法进行总结&#xff0c;包括meanshift算法原理以及公式推导&#xff0c;图解&…
阅读更多...
基于MeanShift的目标跟踪算法及实现

基于MeanShift的目标跟踪算法及实现

这次将介绍基于MeanShift的目标跟踪算法&#xff0c;首先谈谈简介&#xff0c;然后给出算法实现流程&#xff0c;最后实现了一个单目标跟踪的MeanShift算法【matlab/c两个版本】 csdn贴公式比较烦&#xff0c;原谅我直接截图了… 一、简介 首先扯扯无参密度估计理论&#xff0c…
阅读更多...
聚类算法：Mean Shift

聚类算法：Mean Shift

目录 简介 mean shift 算法理论 Mean Shift算法原理 算法步骤 算法实现 其他 聚类算法之Mean Shift Mean Shift算法理论 Mean Shift向量 核函数 引入核函数的Mean Shift向量 聚类动画演示 Mean Shift的代码实现 算法的Python实现 scikit-learn MeanShift演示 s…
阅读更多...
推荐文章

Copyright @ 2022~2023