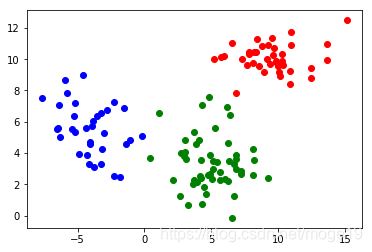
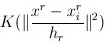Python实现Mean Shift聚类算法

article/2025/11/6 16:32:37

Mean Shift算法，又称均值聚类算法，聚类中心是通过在给定区域中的样本均值确定的，通过不断更新聚类中心，直到聚类中心不再改变为止，在聚类、图像平滑、分割和视频跟踪等方面有广泛的运用。

Mean Shift向量

对于给定的n维空间 R n R^n Rn中的m个样本点 X ( i ) , i = 1 , . . . , m X^{(i)},i=1,...,m X(i),i=1,...,m对于其中的一个样本X，其Mean Shift向量为：
M h ( X ) = 1 k ∑ X ( i ) ϵ S k ( X ( i ) − X ) M_h(X) = \frac{1}{k}\sum_{X^{(i)}\epsilon S_{k}} (X^{(i)}-X) Mh​(X)=k1​X(i)ϵSk​∑​(X(i)−X)
其中 S h S_h Sh​指的是一个半径为h的高维球区域，定义为：
S h ( x ) = ( y ∣ ( y − x ) ( y − x ) T ≤ h 2 S_h (x) = (y|(y-x)(y-x)^T \leq h^2 Sh​(x)=(y∣(y−x)(y−x)T≤h2

Mean Shift算法原理

步骤1：在指定区域内计算出每个样本点漂移均值；
步骤2：移动该点到漂移均值处；
步骤3：重复上述过程；
步骤4：当满足条件时，退出

Mean Shift算法流程

（1) 计算 m h ( X ) m_h(X) mh​(X);
（2）令 X = m h ( X ) X = m_h(X) X=mh​(X);
（3） 如果 ∣ ∣ m h ( X ) − X ∣ ∣ < ε ||m_h(X) -X||<\varepsilon ∣∣mh​(X)−X∣∣<ε，结束循环，否则重复上述步骤。
Mean Shift向量：
M h ( X ) = ∑ i = 1 n [ K ( X ( i ) − X h ) ∗ ( X ( i ) − X ) ] ∑ i = 1 n [ K ( X ( i ) − X h ) ] M_h(X)=\frac{\sum_{i=1} ^n[K(\frac{X^{(i)}-X}{h})*(X^{(i)}-X)]}{\sum_{i=1}^n[K(\frac{X^{(i)}-X}{h})]} Mh​(X)=∑i=1n​[K(hX(i)−X​)]∑i=1n​[K(hX(i)−X​)∗(X(i)−X)]​
= ∑ i = 1 n [ K ( X ( i ) − X h ) ∗ X ( i ) ] ∑ i = 1 n [ K ( X ( i ) − X h ) ] − X =\frac{\sum_{i=1} ^n[K(\frac{X^{(i)-X}}{h})*X^{(i)}]}{\sum_{i=1}^n[K(\frac{X^{(i)}-X}{h})]}- X =∑i=1n​[K(hX(i)−X​)]∑i=1n​[K(hX(i)−X​)∗X(i)]​−X
记 m h ( x ) = ∑ i = 1 n [ K ( X ( i ) − X h ) ∗ X ( i ) ] ∑ i = 1 n [ K ( X ( i ) − X h ) ] m_h(x)=\frac{\sum_{i=1} ^n[K(\frac{X^{(i)-X}}{h})*X^{(i)}]}{\sum_{i=1}^n[K(\frac{X^{(i)}-X}{h})]} mh​(x)=∑i=1n​[K(hX(i)−X​)]∑i=1n​[K(hX(i)−X​)∗X(i)]​则上式变成：
M h ( X ) = m h ( X ) − X M_h(X) = m_h(X) - X Mh​(X)=mh​(X)−X
且
K ( X ( i ) − X h ) = 1 2 π h e ( x 1 − x 2 ) 2 2 h 2 K(\frac{X^{(i)-X}}{h}) = \frac{1}{\sqrt{2\pi}h}e^{\frac{(x_1-x_2)^2}{2h^2}} K(hX(i)−X​)=2π ​h1​e2h2(x1​−x2​)2​
为高斯核函数。

Python实现

（1）计算两个点的欧式距离：

def euclidean_dist(pointA, pointB):'''计算欧式距离input:  pointA(mat):A点的坐标pointB(mat):B点的坐标output: math.sqrt(total):两点之间的欧式距离'''# 计算pointA和pointB之间的欧式距离total = (pointA - pointB) * (pointA - pointB).Treturn math.sqrt(total)  # 欧式距离

（2）计算高斯核函数：

def gaussian_kernel(distance, bandwidth):'''高斯核函数input:  distance(mat):欧式距离bandwidth(int):核函数的带宽output: gaussian_val(mat):高斯函数值'''m = np.shape(distance)[0]  # 样本个数right = np.mat(np.zeros((m, 1)))  # mX1的矩阵for i in range(m):right[i, 0] = (-0.5 * distance[i] * distance[i].T) / (bandwidth * bandwidth)right[i, 0] = np.exp(right[i, 0])left = 1 / (bandwidth * math.sqrt(2 * math.pi))gaussian_val = left * rightreturn gaussian_val

（3）计算均值漂移点

def shift_point(point, points, kernel_bandwidth):'''计算均值漂移点input:  point(mat)需要计算的点points(array)所有的样本点kernel_bandwidth(int)核函数的带宽output: point_shifted(mat)漂移后的点'''points = np.mat(points)m = np.shape(points)[0]  # 样本的个数# 计算距离point_distances = np.mat(np.zeros((m, 1)))for i in range(m):point_distances[i, 0] = euclidean_dist(point, points[i])# 计算高斯核        point_weights = gaussian_kernel(point_distances, kernel_bandwidth)  # mX1的矩阵# 计算分母all_sum = 0.0for i in range(m):all_sum += point_weights[i, 0]# 均值偏移point_shifted = point_weights.T * points / all_sumreturn point_shifted

（4）迭代更新漂移均值（训练过程）

def train_mean_shift(points, kenel_bandwidth=2):'''训练Mean shift模型input:  points(array):特征数据kenel_bandwidth(int):核函数的带宽output: points(mat):特征点mean_shift_points(mat):均值漂移点group(array):类别'''mean_shift_points = np.mat(points)max_min_dist = 1iteration = 0  # 训练的代数m = np.shape(mean_shift_points)[0]  # 样本的个数need_shift = [True] * m  # 标记是否需要漂移# 计算均值漂移向量while max_min_dist > MIN_DISTANCE:max_min_dist = 0iteration += 1print("\titeration : " + str(iteration))for i in range(0, m):# 判断每一个样本点是否需要计算偏移均值if not need_shift[i]:continuep_new = mean_shift_points[i]p_new_start = p_newp_new = shift_point(p_new, points, kenel_bandwidth)  # 对样本点进行漂移dist = euclidean_dist(p_new, p_new_start)  # 计算该点与漂移后的点之间的距离if dist > max_min_dist:max_min_dist = distif dist < MIN_DISTANCE:  # 不需要移动need_shift[i] = Falsemean_shift_points[i] = p_new# 计算最终的groupgroup = group_points(mean_shift_points)  # 计算所属的类别return np.mat(points), mean_shift_points, group

（5）数据源：

10.91079039	8.389412017
9.875001645	9.9092509
7.8481223	10.4317483
8.534122932	9.559085609
10.38316846	9.618790857
8.110615952	9.774717608
10.02119468	9.538779622
9.37705852	9.708539909
7.670170335	9.603152306
10.94308287	11.76207349
9.247308233	10.90210555
9.54739729	11.36170176
7.833343667	10.363034
10.87045922	9.213348128
8.228513384	10.46791102
12.48299028	9.421228147
6.557229658	11.05935349
7.264259221	9.984256737
4.801721592	7.557912927
6.861248648	7.837006973
13.62724419	10.94830031
13.6552565	9.924983717
9.606090699	10.29198795
12.43565716	8.813439258
10.0720656	9.160571589
8.306703028	10.4411646
8.772436599	10.84579091
9.841416158	9.848307202
15.11169184	12.48989787
10.2774241	9.85657011
10.1348076	8.892774944
8.426586093	11.30023345
9.191199877	9.989869949
5.933268578	10.21740004
9.666055456	10.68814946
5.762091216	10.12453436
5.224273746	9.98492559
10.26868537	10.31605475
10.92376708	10.93351512
8.935799678	9.181397458
2.978214427	3.835470435
4.91744201	2.674339991
3.024557256	4.807509213
3.019226157	4.041811881
4.131521545	2.520604653
0.411345842	3.655696597
5.266443567	5.594882041
4.62354099	1.375919061
5.67864342	2.757973123
3.905462712	2.141625079
8.085352646	2.58833713
6.852035583	3.610319053
4.230846663	3.563377115
6.042905325	2.358886853
4.20077289	2.382387946
4.284037893	7.051142553
3.820640884	4.607385052
5.417685111	3.436339164
8.21146303	3.570609885
6.543095544	-0.150071185
9.217248861	2.40193675
6.673038102	3.307612539
4.043040861	4.849836388
3.704103266	2.252629794
4.908162271	3.870390681
5.656217904	2.243552275
5.091797066	3.509500134
6.334045598	3.517609974
6.820587567	3.871837206
7.209440437	2.853110887
2.099723775	2.256027992
4.720205587	2.620700716
6.221986574	4.665191116
5.076992534	2.359039927
3.263027769	0.652069899
3.639219475	2.050486686
7.250113206	2.633190935
4.28693774	0.741841034
4.489176633	1.847389784
6.223476314	2.226009922
2.732684384	4.026711236
6.704126155	1.241378687
6.406730922	6.430816427
3.082162445	3.603531758
3.719431124	5.345215168
6.190401933	6.922594241
8.101883247	4.283883063
2.666738151	1.251248672
5.156253707	2.957825121
6.832208664	3.004741194
-1.523668483	6.870939176
-6.278045454	5.054520751
-4.130089867	3.308967776
-2.298773883	2.524337553
-0.186372986	5.059834391
-5.184077845	5.32761477
-5.260618656	6.373336994
-4.067910691	4.56450199
-4.856398444	3.94371169
-5.169024046	7.199650795
-2.818717016	6.775475264
-3.013197129	5.307372667
-1.840258223	2.473016216
-3.806016495	3.099383642
-1.353873198	4.60008787
-5.422829607	5.540632064
-3.571899549	6.390529804
-4.037978273	4.70568099
-1.110354346	4.809405537
-3.8378779	6.029098753
-6.55038578	5.511809253
-5.816344971	7.813937668
-4.626894927	8.979880178
-3.230779355	3.295580582
-4.333569224	5.593364339
-3.282896829	6.590185797
-7.646892109	7.527347421
-6.461822847	5.62944836
-6.368216425	7.083861849
-4.284758729	3.842576327
-2.29626659	7.288576999
1.101278199	6.548796127
-5.927942727	8.655087775
-3.954602311	5.733640188
-3.160876539	4.267409415

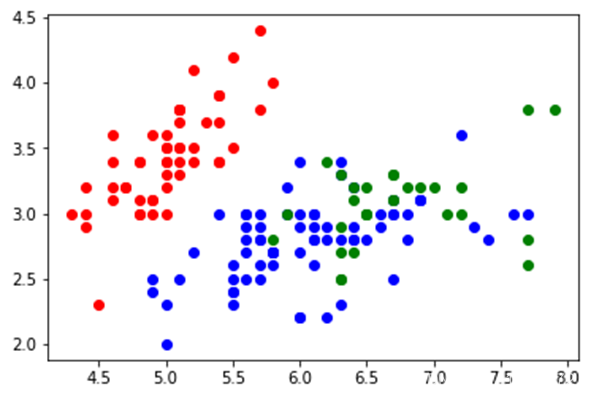
完整代码

# -*- coding: utf-8 -*-
"""
Created on Sun Oct 14 21:52:09 2018@author: ASUS
"""
import math
import numpy as np
import matplotlib.pyplot as plt
MIN_DISTANCE = 0.000001  # mini errordef load_data(path, feature_num=2):'''导入数据input:  path(string)文件的存储位置feature_num(int)特征的个数output: data(array)特征'''f = open(path)  # 打开文件data = []for line in f.readlines():lines = line.strip().split("\t")data_tmp = []if len(lines) != feature_num:  # 判断特征的个数是否正确continuefor i in range(feature_num):data_tmp.append(float(lines[i]))data.append(data_tmp)f.close()  # 关闭文件return datadef gaussian_kernel(distance, bandwidth):'''高斯核函数input:  distance(mat):欧式距离bandwidth(int):核函数的带宽output: gaussian_val(mat):高斯函数值'''m = np.shape(distance)[0]  # 样本个数right = np.mat(np.zeros((m, 1)))  # mX1的矩阵for i in range(m):right[i, 0] = (-0.5 * distance[i] * distance[i].T) / (bandwidth * bandwidth)right[i, 0] = np.exp(right[i, 0])left = 1 / (bandwidth * math.sqrt(2 * math.pi))gaussian_val = left * rightreturn gaussian_valdef shift_point(point, points, kernel_bandwidth):'''计算均值漂移点input:  point(mat)需要计算的点points(array)所有的样本点kernel_bandwidth(int)核函数的带宽output: point_shifted(mat)漂移后的点'''points = np.mat(points)m = np.shape(points)[0]  # 样本的个数# 计算距离point_distances = np.mat(np.zeros((m, 1)))for i in range(m):point_distances[i, 0] = euclidean_dist(point, points[i])# 计算高斯核        point_weights = gaussian_kernel(point_distances, kernel_bandwidth)  # mX1的矩阵# 计算分母all_sum = 0.0for i in range(m):all_sum += point_weights[i, 0]# 均值偏移point_shifted = point_weights.T * points / all_sumreturn point_shifteddef euclidean_dist(pointA, pointB):'''计算欧式距离input:  pointA(mat):A点的坐标pointB(mat):B点的坐标output: math.sqrt(total):两点之间的欧式距离'''# 计算pointA和pointB之间的欧式距离total = (pointA - pointB) * (pointA - pointB).Treturn math.sqrt(total)  # 欧式距离def group_points(mean_shift_points):'''计算所属的类别input:  mean_shift_points(mat):漂移向量output: group_assignment(array):所属类别'''group_assignment = []m, n = np.shape(mean_shift_points)index = 0index_dict = {}for i in range(m):item = []for j in range(n):item.append(str(("%5.2f" % mean_shift_points[i, j])))item_1 = "_".join(item)if item_1 not in index_dict:index_dict[item_1] = indexindex += 1for i in range(m):item = []for j in range(n):item.append(str(("%5.2f" % mean_shift_points[i, j])))item_1 = "_".join(item)group_assignment.append(index_dict[item_1])return group_assignmentdef train_mean_shift(points, kenel_bandwidth=2):'''训练Mean shift模型input:  points(array):特征数据kenel_bandwidth(int):核函数的带宽output: points(mat):特征点mean_shift_points(mat):均值漂移点group(array):类别'''mean_shift_points = np.mat(points)max_min_dist = 1iteration = 0  # 训练的代数m = np.shape(mean_shift_points)[0]  # 样本的个数need_shift = [True] * m  # 标记是否需要漂移# 计算均值漂移向量while max_min_dist > MIN_DISTANCE:max_min_dist = 0iteration += 1print("\titeration : " + str(iteration))for i in range(0, m):# 判断每一个样本点是否需要计算偏移均值if not need_shift[i]:continuep_new = mean_shift_points[i]p_new_start = p_newp_new = shift_point(p_new, points, kenel_bandwidth)  # 对样本点进行漂移dist = euclidean_dist(p_new, p_new_start)  # 计算该点与漂移后的点之间的距离if dist > max_min_dist:max_min_dist = distif dist < MIN_DISTANCE:  # 不需要移动need_shift[i] = Falsemean_shift_points[i] = p_new# 计算最终的groupgroup = group_points(mean_shift_points)  # 计算所属的类别return np.mat(points), mean_shift_points, groupdef save_result(file_name, data):'''保存最终的计算结果input:  file_name(string):存储的文件名data(mat):需要保存的文件'''f = open(file_name, "w")m, n = np.shape(data)for i in range(m):tmp = []for j in range(n):tmp.append(str(data[i, j]))f.write("\t".join(tmp) + "\n")f.close()if __name__ == "__main__":color=['.r','.g','.b','.y']#颜色种类# 导入数据集print ("----------1.load data ------------")data = load_data("data", 2)N = len(data)# 训练，h=2print ("----------2.training ------------")points, shift_points, cluster = train_mean_shift(data, 2)# 保存所属的类别文件# save_result("center_1", shift_points) data = np.array(data)for i in range(N):if cluster[i]==0:plt.plot(data[i, 0], data[i, 1],'ro')elif cluster[i]==1:plt.plot(data[i, 0], data[i, 1],'go')elif cluster[i]==2:plt.plot(data[i, 0], data[i, 1],'bo')plt.show()

运行结果

在这里插入图片描述


http://chatgpt.dhexx.cn/article/a1y41a2M.shtml

相关文章

mean shift 跟踪算法

mean shift 跟踪算法

说明一&#xff1a; Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其偏移均值,然后以此为新的起始点,继续移动,直到满足一定的条件结束. 1. Meanshift推导 给定d维空间Rd的n个样本点 ,i1,…,n,在空间中任选一点x&#xff0c;那么Mean Shift向量…
阅读更多...
Python实现Mean Shift算法

Python实现Mean Shift算法

声明&#xff1a;代码的运行环境为Python3。Python3与Python2在一些细节上会有所不同&#xff0c;希望广大读者注意。本博客以代码为主&#xff0c;代码中会有详细的注释。相关文章将会发布在我的个人博客专栏《Python从入门到深度学习》&#xff0c;欢迎大家关注~ 在K-Means算…
阅读更多...
meanshift算法 java_Meanshift，聚类算法

meanshift算法 java_Meanshift，聚类算法

记得刚读研究生的时候&#xff0c;学习的第一个算法就是meanshift算法&#xff0c;所以一直记忆犹新&#xff0c;今天和大家分享一下Meanshift算法&#xff0c;如有错误&#xff0c;请在线交流。 Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其…
阅读更多...
保边滤波之Mean shift filter

保边滤波之Mean shift filter

Mean shift filter 目录 Mean shift filter 一、算法原理 二、练手实现的算法代码如下&#xff1a; 三、实现结果 一、算法原理 在OpenCV中&#xff0c;meanshift filter函数为 pyrMeanShiftFiltering&#xff0c; 它的函数调用格式如下&#xff1a; C: void pyrMeanShif…
阅读更多...
mean shift

mean shift

参考&#xff1a; http://blog.csdn.net/google19890102/article/details/51030884 http://www.cvvision.cn/5778.html https://wenku.baidu.com/view/5862334827d3240c8447ef40.html http://blog.csdn.net/qq_23968185/article/details/51804574 https://www.cnblogs.com…
阅读更多...
机器学习算法原理与实践（二）、meanshift算法图解以及在图像聚类、目标跟踪中的应用

机器学习算法原理与实践（二）、meanshift算法图解以及在图像聚类、目标跟踪中的应用

【原创】Liu_LongPo 转载请注明出处 【CSDN】http://blog.csdn.net/llp1992 最近在关注跟踪这一块的算法&#xff0c;对于meanshift的了解也是来自论文和博客&#xff0c;本博客将对meanshift算法进行总结&#xff0c;包括meanshift算法原理以及公式推导&#xff0c;图解&…
阅读更多...
基于MeanShift的目标跟踪算法及实现

基于MeanShift的目标跟踪算法及实现

这次将介绍基于MeanShift的目标跟踪算法&#xff0c;首先谈谈简介&#xff0c;然后给出算法实现流程&#xff0c;最后实现了一个单目标跟踪的MeanShift算法【matlab/c两个版本】 csdn贴公式比较烦&#xff0c;原谅我直接截图了… 一、简介 首先扯扯无参密度估计理论&#xff0c…
阅读更多...
聚类算法：Mean Shift

聚类算法：Mean Shift

目录 简介 mean shift 算法理论 Mean Shift算法原理 算法步骤 算法实现 其他 聚类算法之Mean Shift Mean Shift算法理论 Mean Shift向量 核函数 引入核函数的Mean Shift向量 聚类动画演示 Mean Shift的代码实现 算法的Python实现 scikit-learn MeanShift演示 s…
阅读更多...
meanshift算法通俗讲解

meanshift算法通俗讲解

这几天学习《学习OpenCV》中的第十章运动跟踪&#xff0c;里面讲到了meanshift算法&#xff0c;根据书上所讲实在难以理解&#xff0c;meanshift在运动跟踪这个过程中到底起到什么作用&#xff0c;于是经过几天不断地看相关资料和别人的博客文章&#xff0c;慢慢思路清晰了&…
阅读更多...
机器学习实验 - MeanShift聚类

机器学习实验 - MeanShift聚类

目录 一、报告摘要1.1 实验要求1.2 实验思路1.3 实验结论 二、实验内容2.1 方法介绍2.2 实验细节2.2.1 实验环境2.2.2 实验过程2.2.3 实验与理论内容的不同点 2.3 实验数据介绍2.4 评价指标介绍2.5 实验结果分析 三、总结及问题说明四、参考文献附录&#xff1a;实验代码 报告内…
阅读更多...
聚类 之 MeanShift

聚类 之 MeanShift

文章目录 Meanshift 聚类基本原理Meanshift 聚类流程简述实例演示MeanShift聚类简易应用示例总结拓展阅读 上篇博客介绍了基于距离的K-Means聚类&#xff0c;这次给大家推荐一个基于密度的聚类算法&#xff1a;Meanshift&#xff08;均值漂移&#xff09;。 Meanshift 聚类基本…
阅读更多...
Muduo源码剖析

Muduo源码剖析

1、总体流程 1. acceptor 进行listen阶段后&#xff0c; 往channel中注册可读事件。 2. acceptor可读处理中生成TcpConnection指针&#xff0c;通过EventloopThreadPool 轮询出其中一个线程的eventloop, 并将此TcpConnection的可读、可写等事件注册到自己Channel&#xff08;ev…
阅读更多...
Muduo - Reactor模式

Muduo - Reactor模式

Muduo - Reactor模式 一、Reactor 是什么 wiki的中文定义&#xff1a;Reactor模式是事件驱动的&#xff0c;有一个或多个并发输入源&#xff0c;有一个Service Handler&#xff0c;有多个Request Handler&#xff0c;这个Service Handler会同步的将输入的请求&#xff08;Even…
阅读更多...
muduo网络库——ThreadPool

muduo网络库——ThreadPool

模型 源码分析 1&#xff09;接口 class ThreadPool : noncopyable {public:typedef std::function<void ()> Task;explicit ThreadPool(const string& nameArg string("ThreadPool"));~ThreadPool();void setMaxQueueSize(int maxSize) { maxQueueSize…
阅读更多...
muduo网络库——Channel

muduo网络库——Channel

模型 实现流程&#xff1a; 前面已经介绍了EPoller类&#xff0c;EPoller主要监听的是Channel对象&#xff0c;每一个Channel对象会绑定一个文件描述符&#xff08;fd_&#xff09;&#xff0c;fd_上绑定要监听的事件。当epoll监听到就绪事件时&#xff0c;会将就绪事件添加到…
阅读更多...
muduo源码分析之Buffer

muduo源码分析之Buffer

这一次我们来分析下muduo中Buffer的作用&#xff0c;我们知道&#xff0c;当我们客户端向服务器发送数据时候&#xff0c;服务器就会读取我们发送的数据&#xff0c;然后进行一系列处理&#xff0c;然后再发送到其他地方&#xff0c;在这里我们想象一下最简单的EchoServer服务器…
阅读更多...
从实例看muduo网络库各模块交互过程

从实例看muduo网络库各模块交互过程

文章目录 muduo网络库的核心代码模块各模块功能解释ChannelPollerEpollPoller EventLoopEventLoopThreadEventLoopThreadPoolTcpServerTcpConnection 从实际应用出发 muduo网络库的核心代码模块 1、channel 2、Poller 和它的子类 EpollPoller 3、EventLoop 4、Thread、EventLo…
阅读更多...
muduo总结

muduo总结

本文重点在muduo TcpServer的启动&#xff0c;I/O线程池的启动&#xff0c;以及各种回调 文章目录 baseAsyncLogging.{h,cc}Atomic.hBlockinQueue.hBoundedBlockinQueue.hCondition.hcopyable.hCountDownLatch.{h,cc}Date.{h,cc}Exception.{h,cc}Logging.{h,cc}Mutex.hProcess…
阅读更多...
muduo网络库——日志处理

muduo网络库——日志处理

测试程序 #include "muduo/base/AsyncLogging.h" #include "muduo/base/Logging.h" #include "muduo/base/Timestamp.h"#include <stdio.h> #include <sys/resource.h> #include <unistd.h>off_t kRollSize 500*1000*1000;m…
阅读更多...
Muduo日志模块详解

Muduo日志模块详解

Muduo日志模块解析 图片取自muduo网络库源码解析(1):多线程异步日志库(上)_李兆龙的技术博客_51CTO博客也是很好的日志讲解博客,这篇讲解流程基本上和它差不多,并且写的比我条理清楚很多 AppendFile::append() 这个函数是日志写入文件的最终函数,并且AppendFile这个类里面也是…
阅读更多...
推荐文章

Copyright @ 2022~2023