一、树的平衡性

•  为了能以较快的时间O(logN)来操作一棵树,我们需要保证树总是平衡的:
  • 至少大部分是平衡的,那么时间复杂度也是接近O(logN)的
  • 也就是说树中每个节点左边的子孙节点的个数应该尽可能的等于右边的子孙节点的个数.
  • 常见的平衡树有哪些呢?
• AVL树:
  • AVL树是最早的一种平衡树.它有些办法保持树的平衡(每个节点多存储了一个额外的数据)
  • 因为AVL树是平衡的,所以时间复杂度也是O(IogN).
  • 但是,每次插入/删除操作相对于红黑树效率都不高,所以整体效率不如红黑树
• 红黑树:
  • 红黑树也通过一些特性来保持树的平衡.
  • 因为是平衡树,所以时间复杂度也是在O(logN).
  • 另外插入/删除等操作,红黑树的性能要优于AVL树,所以现在平衡树的应用基本都是红黑树.

二、认识红黑树 

红黑树的规则 

•  红黑树,除了符合二叉搜索树的基本规则外，还添加了一下特性: 

1. 节点是红色或黑色。
2. .根节点是黑色。 
3. 每个叶子节点都是黑色的空节点(NIL节点)。
4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

 这些规则会让人一头雾水
        完成搞不懂规则叠加起来,怎么让一棵树平衡的.
        但是它们还是被一些聪明的人发明出来了. 

 

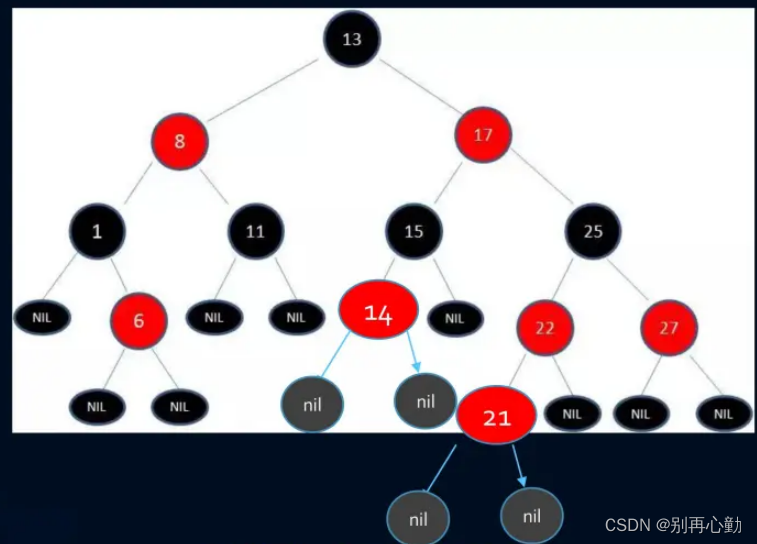
红黑树的相对平衡

 前面的约束，确保了红黑树的关键特性:

• 从根到叶子的最长可能路径，不会超过最短可能路径的两倍长.
• 结果就是这个树基本是平衡的.
• 虽然没有做到绝对的平衡，但是可以保证在最坏的情况下，依然是高效的.

为什么可以做到最长路径不超过最短路径的两倍呢? 

• 性质4决定了路径不能有两个相连的红色节点
• 最短的可能路径都是黑色节点.
• 最长的可能路径是红色和黑色交替.
• 性质5所有路径都有相同数目的黑色节点.
• 这就表明了没有路径能多余任何其他路径的两倍长 

三、红黑树的变换 

变色 

插入一个新节点时，有可能树不再平衡，可以通过三种方式的变换让树保持平衡。  

• 换色 - 左旋转 - 右旋转 

变色： 

• 为了重新符合红黑树的规则，尝试把红色节点变为黑色，或者把黑色节点变为红色。 

首先，需要知道插入的新节点通常都是红色节点。 

• 因为在插入节点为红色的时候，有可能插入一次是不违反红黑树任何规则的
• 而插入黑色节点，必然会导致有一条路径上多了黑色节点，这是很难调整的。
• 红色节点可能导致出现红红相连的情况，但是这种情况可以通过颜色调换和旋转来调整 

旋转

左旋转 

• 逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子。 

 

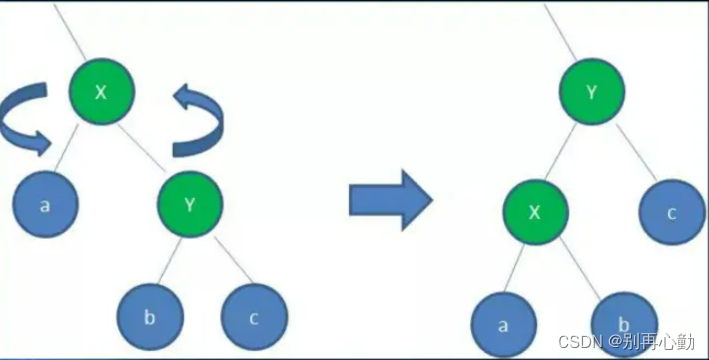
• 图中，身为右孩子的Y取代了X的位置，而X变成了Y的左孩子。此为左旋转。 

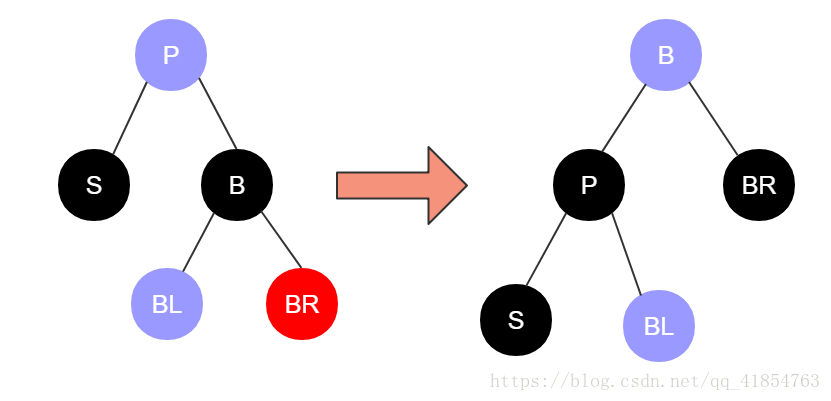
右旋转： 

• 顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子。 

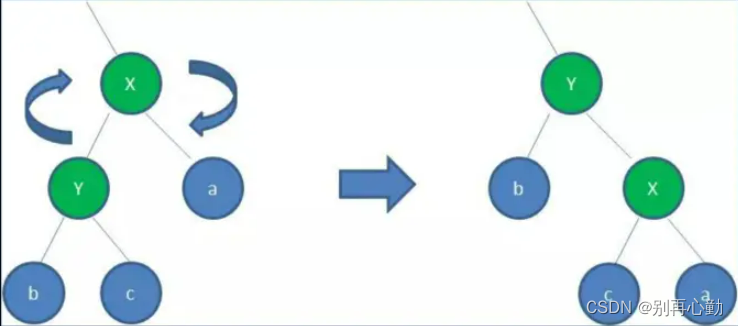
• 图中，身为 左孩子的Y取代了X的位置，而x变成了Y的右孩子。

四、插入操作的情况分析 

插入操作  

• 接下来，讨论一下插入的情况：
  • 设要插入的节点为N，其父节点为P
  • 其祖父节点为G，其父亲的兄弟节点为U(即P和U是一个同一个节点的子节点)。 
• 情况一： 
  • 新节点N位于树的根上，没有父节点。
  • 这种情况下，我们直接将红色变换为黑色即可，这样满足性质2.
• 情况二：
  • 新节点的父节点P是黑色
  • 性质4没有失效(新节点是红色的)，性质5也没有任何问题
  • 尽管新节点N有两个黑色的叶子节点nill，但是新节点N是红色的，所以通过它的路径中黑色节点的个数依然相同，满足性质5
• 情况三：
  • P为红色，U也是红色
  • 父红叔红祖黑 -> 父黑叔黑祖红
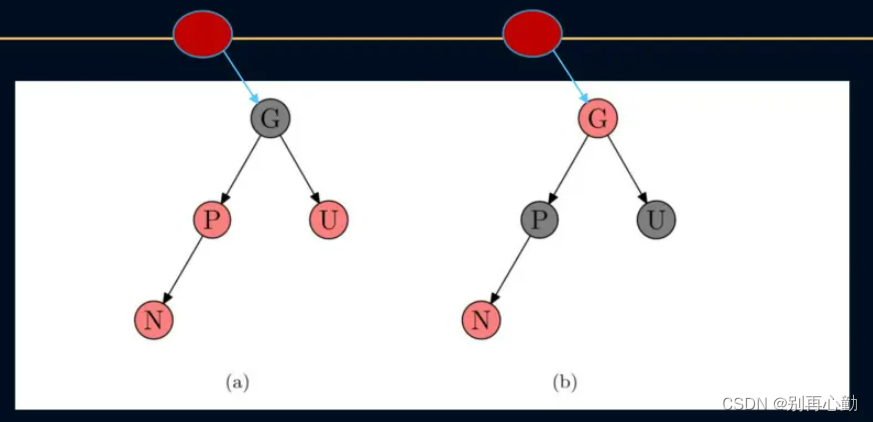
• 操作方案：
  • 将P和U变换为黑色,并且将G变换为红色.
  • 现在新节点N有了一个黑色的父节点P所以每条路径上黑色节点的数目没有改变.
  • 而从更高的路径上，必然都会经过G节点,所以那些路径的黑色节点数目也是不变的.符合性质5.
• 可能出现的问题:
  • 但是, N的祖父节点G的父节点也可能是红色,这就违反了性质3,可以递归的调整颜色.
  • 但是如果递归调整颜色到了根节点,就需要进行旋转了待会儿我们的例子中会遇到这个问题.

 

•  情况四：
  • N的数数U是黑节点，且N是做孩子.父红叔黑祖黑N是左儿子
    • 父黑
    • 祖红
    • 右旋转
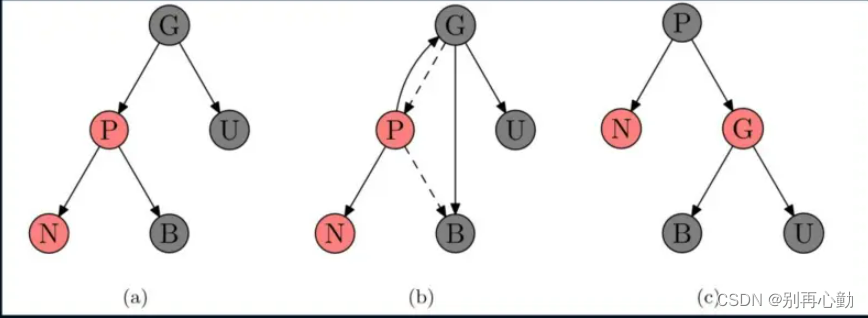
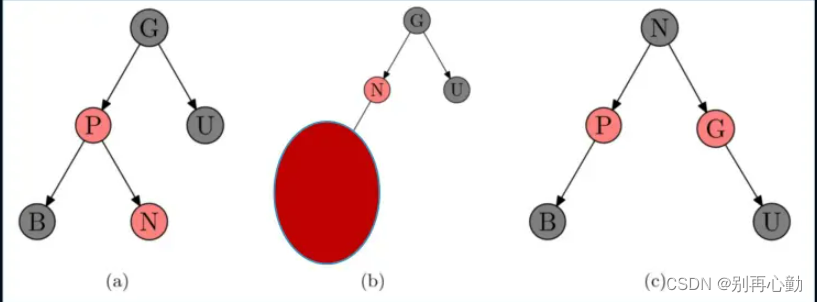
  • 操作方案：
    • 对祖父节点G进行依次右旋转
    • 在旋转查收的树中,以前的父节点P现在是新节点已经以前祖父节点G的父节点.
    • 交换以前的父节点P和祖父节点G的颜色.(P为黑色, G变成红色–G原来一定是黑色，为什么?)
    • B节点向右平移,称为G节点的左子节点.

 

• 情况五：
  • N的叔叔U是黑色节点,且N是有孩子.父红叔黑祖黑,N是右儿子
    • 以P为根,左旋转 
  • 将P作为新插入的红色节点考虑即可->自己变成黑色
    • 祖变成红色
    • 以祖为根,进行右旋转
• 操作方案：
  • 对P节点进行依次左旋转,形成情况四的结果.
  • 对祖父节点G进行一次右旋转，并且改变颜色即可

 

五、红黑树的案例 

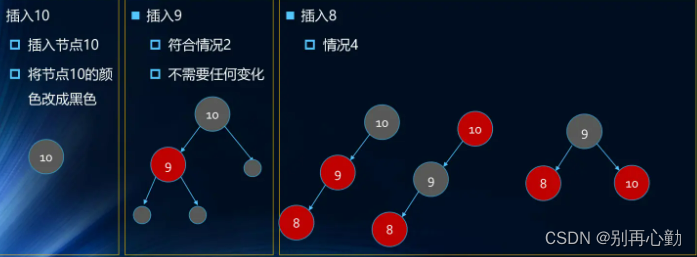
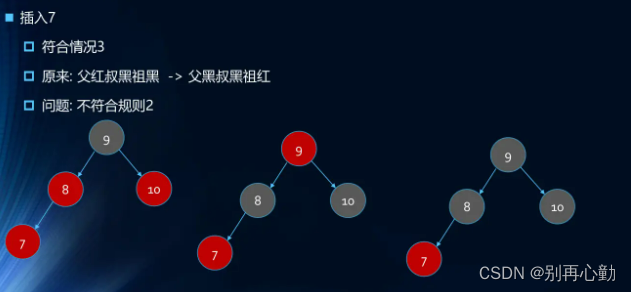
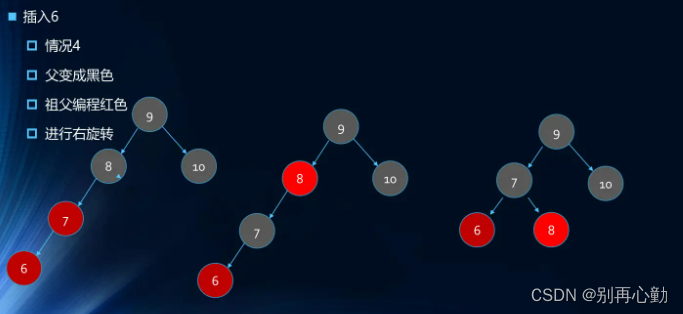
• 案例:1 2 3 4 5 6 7 8 9 10
• 案例:依次插入10 9 8 7 6 5 4 3 2 1

 

 

 

 

 

 

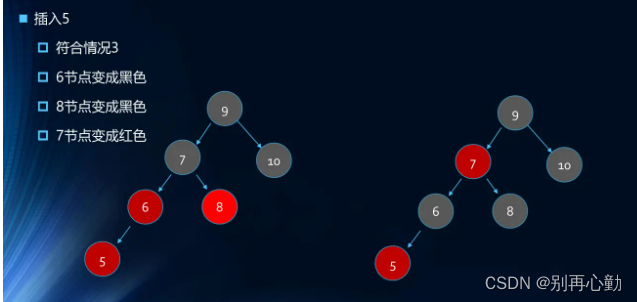
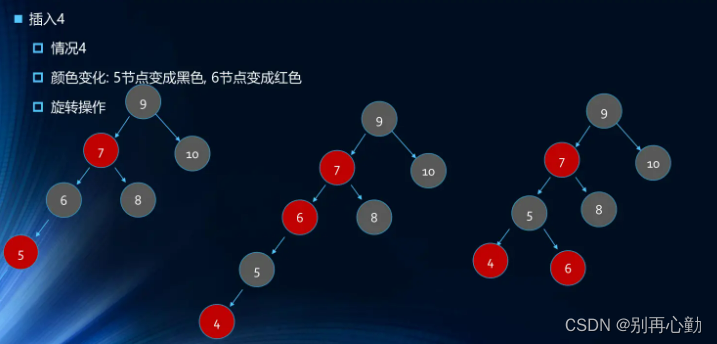
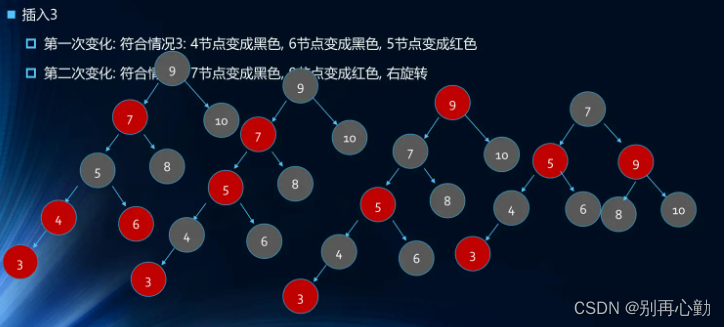
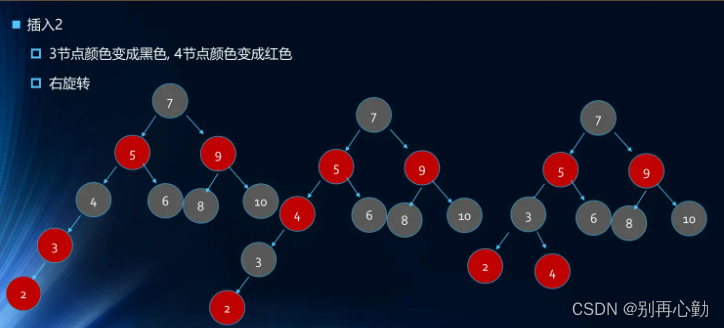
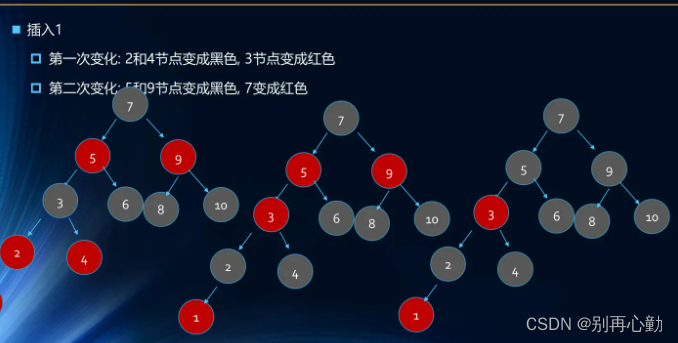
删除&代码 

• 红黑树的删除
  • 我们已经学习过了二叉搜索树的删除操作,比较复杂.
  • 我们已经学习过了红黑树的插入规则,比较复杂.
  • 红黑树的删除操作呢? 
  • 它就需要将两个复杂的操作结合起来考虑,所以难度非常大
• 插入和删除的代码实现:
  • 插入的步骤我们已经一步步的进行了分析.
  • 分析完成后，写出插入的代码并不是很难.
  • 删除也需要按照插入一样,分成很多种情况,然后写出最终的代码形式.