红黑树的性质:
在了解红黑树之前,建议先去了解一下什么是二叉搜索树。
因为红黑树属于二叉搜索树特殊的分支,所以建议先去了解一下二叉搜索树。
二叉搜索树:https://blog.csdn.net/Falling_stars_/article/details/115536511
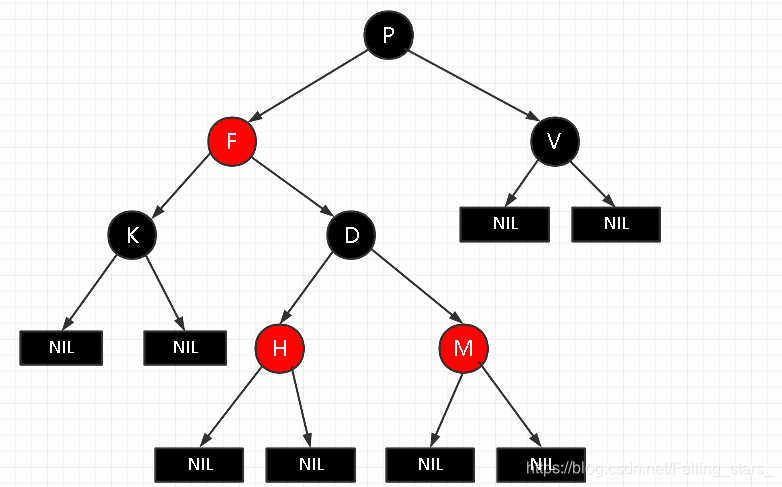
红黑树实例图
性质1:每个节点要么是黑色,要么是红色。
性质2:根节点只能是黑色。
性质3:每个叶子节点(NIL)是黑色。
性质4:每个红色节点的两个子节点一定都是黑色。不能有两个红色节点相连。
性质5:任意一节点到每个叶子节点的路径都包含数量相同的黑结点。俗称:黑高!
从性质5又可以得出:
性质5.1:如果一个节点存在黑子节点,那么该节点肯定有两个子节点
红黑树并不是一个完美平衡二叉搜索树,从图上可以看到,根节点P的左子树显然比右子树高,
但左子树和右子树的黑节点的层数是相等的,
即任意一个节点到每个叶子节点的路径都包含数量相同的黑节点(性质5)。
所以称红黑树这种平衡为黑色完美平衡。
之所以红黑树能自然平衡,就是靠它的三种操作:左旋、右旋和变色。
1.变色:节点的颜色由红变黑或由黑变红。
2.左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
3.右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
左旋动态图
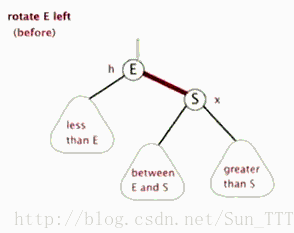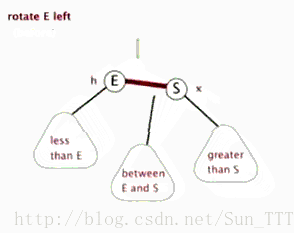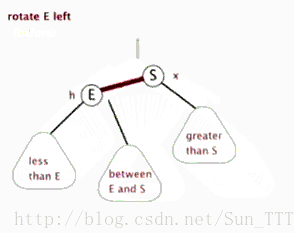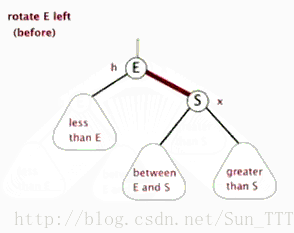
左旋图示

右旋动态图
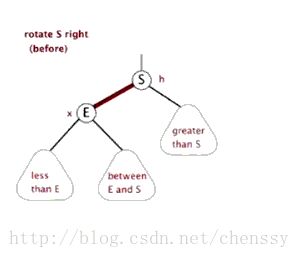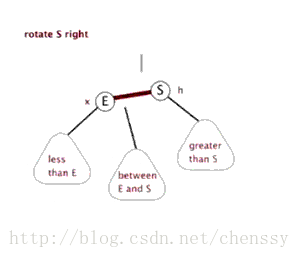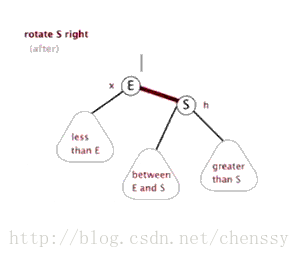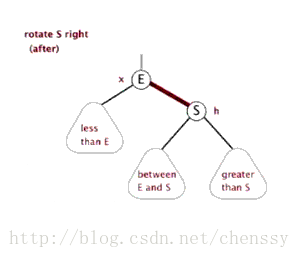
右旋图示

红黑树查找:
其实红黑树查找与二叉搜索树的查找无差别。

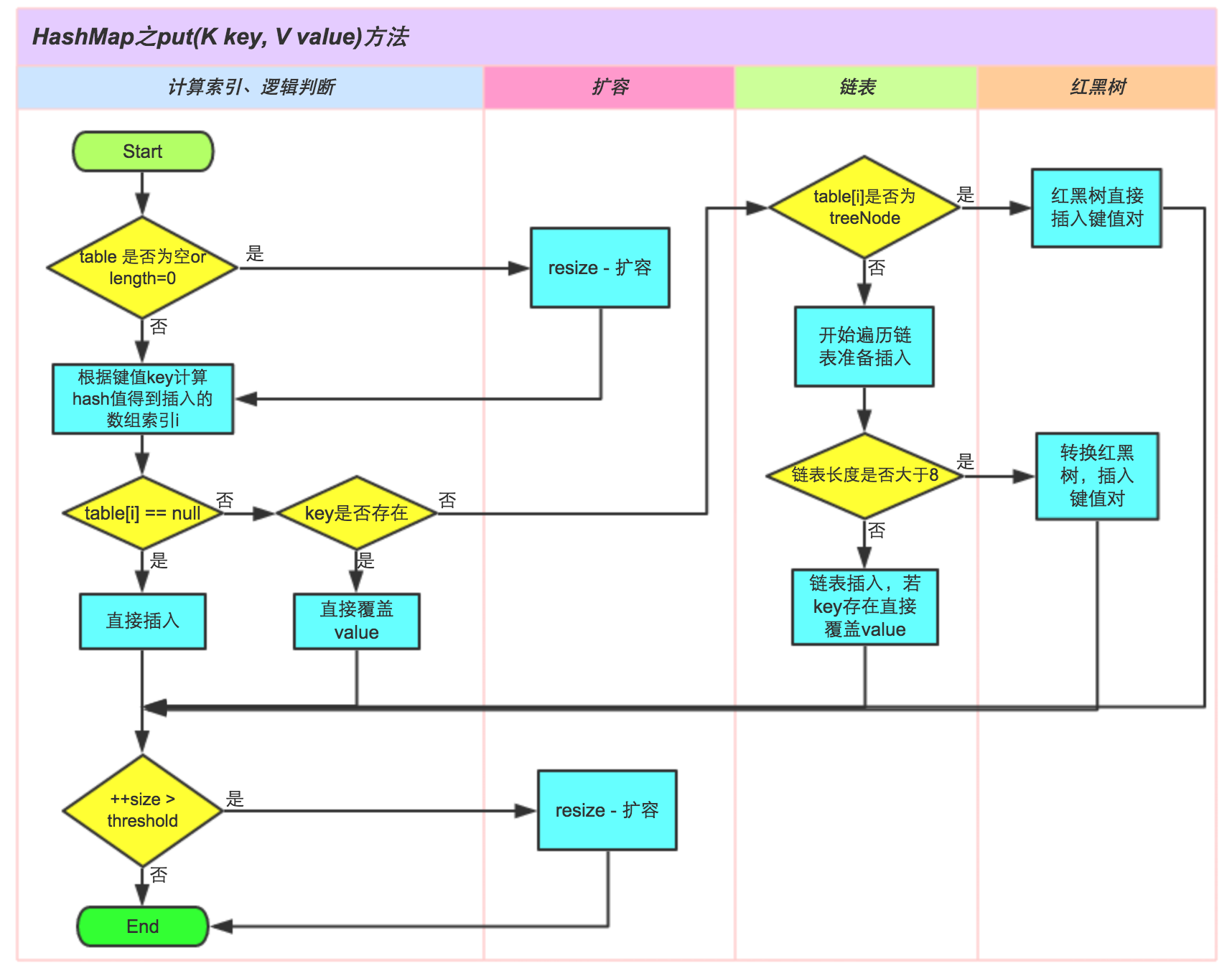
红黑树插入:
插入操作包括两部分:
1.查找插入的位置
2.插入后自平衡
注意:插入节点,必须为红色,因为红色的父节点(如果存在)为黑色节点时,红黑树的黑色平衡没有被破坏,不需要做自平衡操作。
但如果插入节点是黑色,那么插入位置所在的子树黑色节点总是多1,此时必须做自平衡。
如图:
红黑树插入节点情景分析
情景1:红黑树为空树
直接把插入结点作为根节点就可以了
注意:根据红黑树性质2:根节点是黑色的。还需要把插入节点设置为黑色。
情景2:插入节点的Key已经存在
更新当前节点的值,为插入节点的值。也就是覆盖

情景3:插入节点的父节点为黑节点
由于插入的节点是红色的,当插入节点的父节点是黑色时,不会影响红黑树的平衡,直接插入无需做自平衡。

情景4:插入节点的父节点为红色
根据红黑树的性质2:根节点是黑色。
如果插入节点的父节点为红色节点,那么该父节点不可能为根节点,所以插入节点总是存在祖父节点(三代关系)。
根据性质4:每个红色节点的两个子节点一定是黑色的。
不能有两个红色节点相连。
此时会出现两种状态,如图

情景4.1:叔叔节点存在并且为红色节点
根据红黑树性质4:红色节点不能相连 ==》祖父节点肯定为黑色节点:
因为不可能同时存在两个相连的红色节点,那么此时该插入子树的红黑树层数的情况是:黑红红。显然处理方式是把其改为:红黑红
处理:
1.将F和V节点改为黑色
2.将P改为红色
3.将P设置为当前节点,进行后续处理

可以看到,将P设置为红色了,如果P的父节点是黑色,那么无需做处理;
但如果P的父节点是红色,则违反红黑树性质了,所以需要将P设置为当前节点,继续插入操作作自平衡平衡处理,直道平衡为止。
插入情景4.2:叔叔节点不存在或为黑节点,并且节点的父亲节点是祖父节点的左子节点
注意:单纯从插入来看,叔叔节点非红即空(NIL节点),否则破坏了红黑树性质5,此时路径会比其他路径多一个黑色节点。

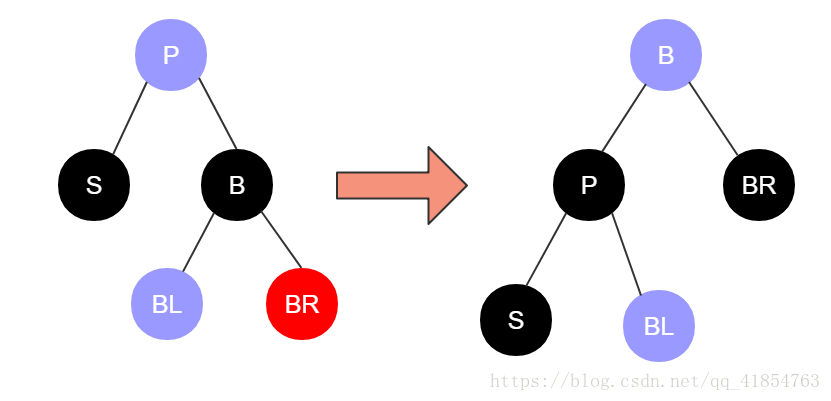
插入情景4.2.1新插入节点,为其父节点的左子节点(LL红色情况)
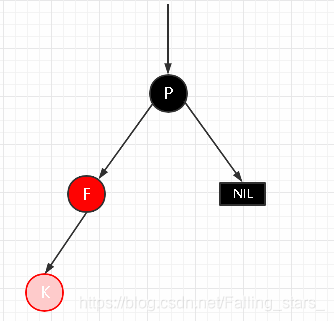
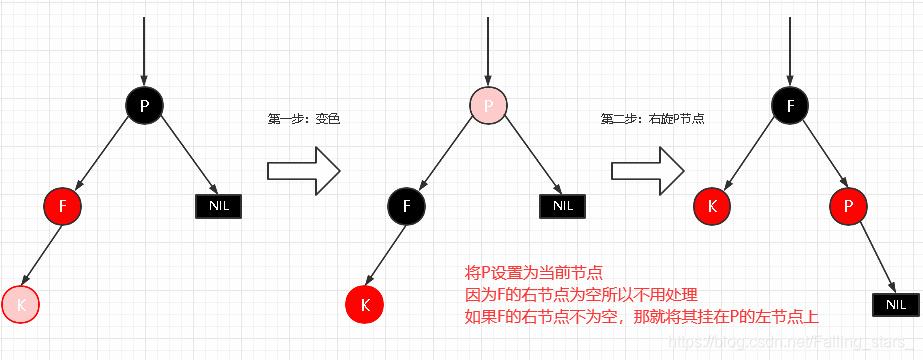
处理:
1.变颜色:将F设置为黑色,将P设置为红色
2.对F节点进行右旋
情景4.2.2:新插入节点,为其父节点的右节点(LR红色情况)

处理:
1.对F进行左旋
2.将F设置为当前节点,得到LL红色情况
3.按照LL红色情况处理(1.变色 2.右旋P节点)

情景4.3:叔叔节点不存在或者为黑节点,并且插入节点的父亲节点是祖父节点的右子节点
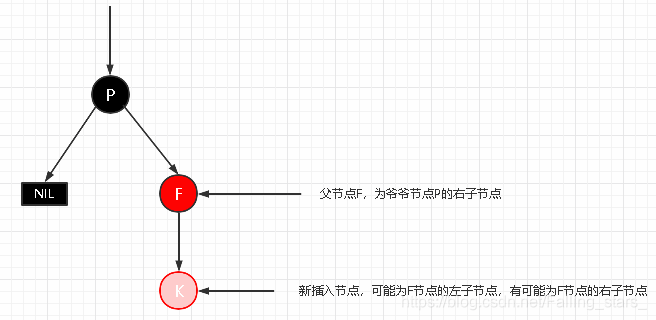
情景4.3.1:新插入节点,为其父节点的右子节点(RR红色情况)

处理:
1.变色:将F设置为黑色,将P设置为红色
2.对P节点进行左旋

情景4.3.2:新插入节点,为其父节点的左子节点(RL红色情况)

处理:
1.对F进行右旋
2.将F设置为当前节点,得到RR红色情况
3.按照RR红色情况处理(1.变色 2.左旋P节点)

红黑树插入案例分析
字有点小,请自行放大观看