解决Gin框架下浏览器(chrome)在setcookie()后不能成功携带cookie的问题

article/2025/9/29 3:42:41

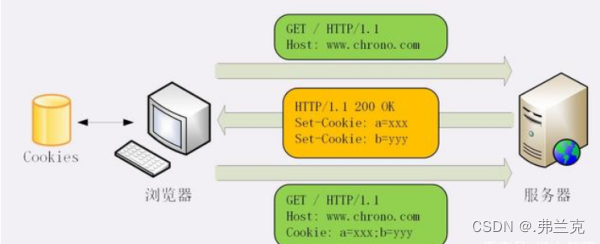
参考gin官网的文档给出的代码：地址在https://gin-gonic.com/zh-cn/docs/examples/cookie/

func CookieMiddleWare() gin.HandlerFunc {return func(c *gin.Context) {cookieValue, err := c.Cookie("cookie")if err != nil {//c.AbortWithStatusJSON(403, gin.H{"message": "get cookie failed..."})fmt.Printf("err happened :%v\n", err)code := utils.GenInviteCode("cookie", 8)c.SetCookie("cookie", code, 3600*24*30, "/", "localhost", false, false)}fmt.Println(cookieValue)c.Next()}
}

打怪历程：
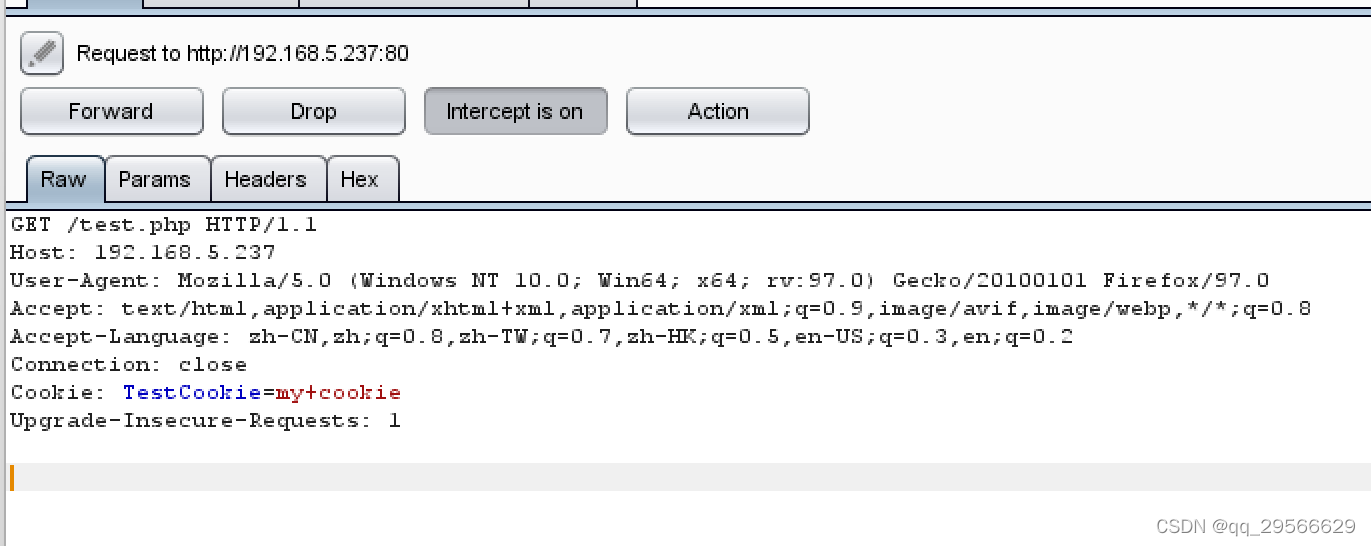
首先按以上代码跑服务然后在浏览器访问本地务:http://127.0.0.1:8090/api/auth/xxx

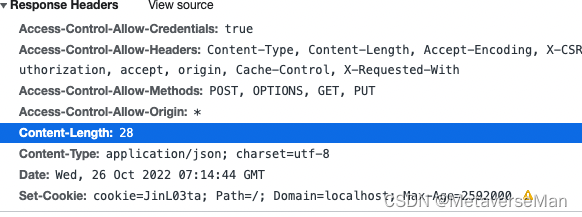
在这里插入图片描述

这个时候浏览器端是没有进行cookie存储的。

刷新，再次发请求，查看请求头的Requests Headers 里是没有cookie这一项的。失败！
回想到samesite相关知识，于是添加samesite设置：

func CookieMiddleWare() gin.HandlerFunc {return func(c *gin.Context) {cookieValue, err := c.Cookie("cookie")if err != nil {//c.AbortWithStatusJSON(403, gin.H{"message": "get cookie failed..."})fmt.Printf("err happened :%v\n", err)code := utils.GenInviteCode("cookie", 8)//setSameSite()要在setCookie()前边, 使用setSameSite()方法的条件是：要将 cookie的secure属性设置为true//c.SetSameSite(4)c.SetSameSite(http.SameSiteNoneMode)c.SetCookie("cookie", code, 3600*24*30, "/", "localhost", false, false}	}

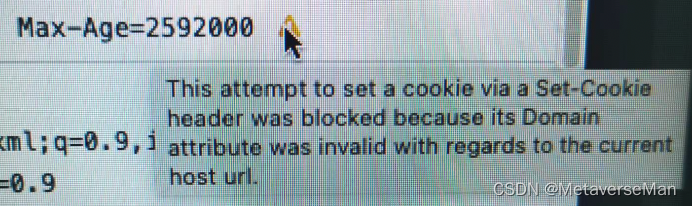
还是会有那个小三角提示符认真读了一下：是domain不对，于是在github上参考了一个三哥的代码：github.com，将domain改为带协议和端口的：“http://localhost:8090”
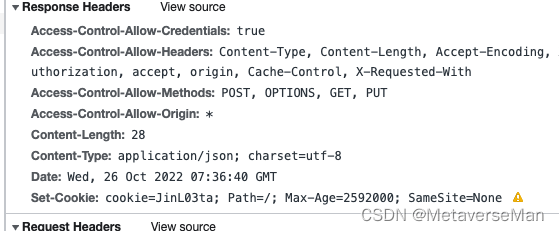
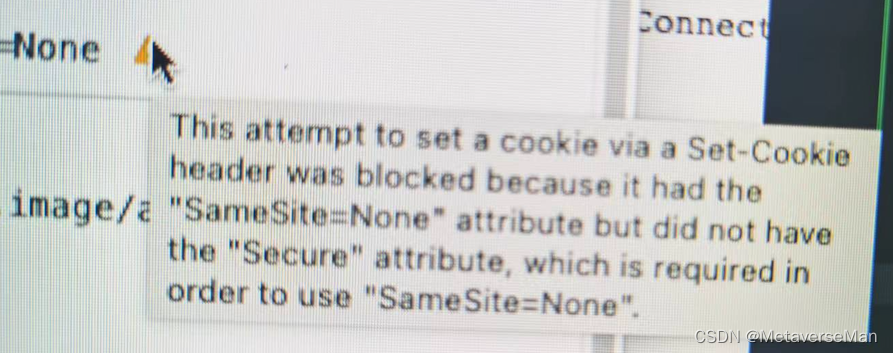
在这里插入图片描述

这次的 Set-Cookie: 里没有domain的相关的内容了，然后末尾的小黄三角符号又说如果启用SameSite就要将cookie的Secure选项选为true 。

c.SetSameSite(http.SameSiteNoneMode)
c.SetCookie("cookie", code, 3600*24*30, "/", "http://localhost:8090", true, false)

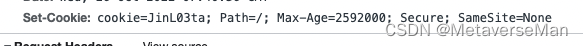
在这里插入图片描述
发现没有小黄三角符号了
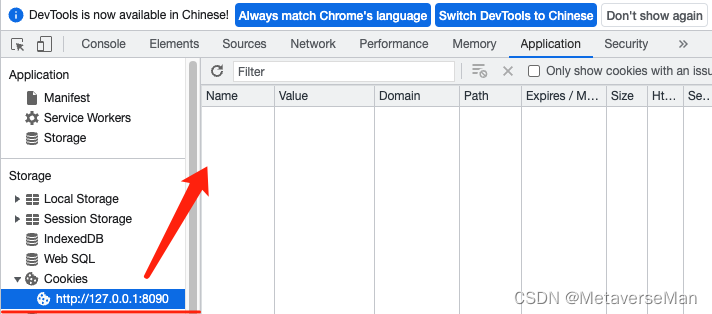
再次查看 application里的cookie

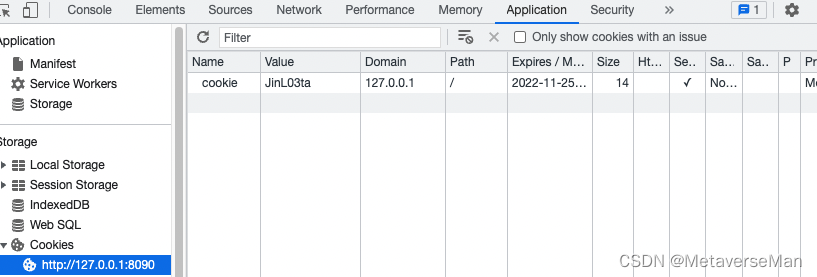
已经有值了。刷新，再次请求

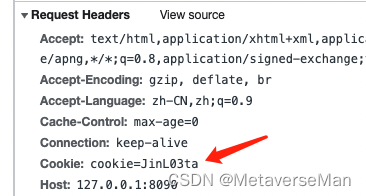
requests headers里已经携带cookie去访问了。问题解决！
同时思考一下这是使用了SameSite相关设置，如果不设置能否正常携带cookie访问呢？
答案是肯定的：
其实只要domain配置对，不启用Secure和samesite也是可以的。
我们在err条件外将cookie生存时间设置为-1,刷新浏览器，将上次的cookie杀死：

//生存时间设置为-1。杀死后记得注释掉
c.SetCookie("cookie", "code", -1, "/", "http://localhost:8090", false, false)

然后尝试不启用Secure和不配置samesite的访问：

func CookieMiddleWare() gin.HandlerFunc {return func(c *gin.Context) {cookieValue, err := c.Cookie("cookie")if err != nil {//c.AbortWithStatusJSON(403, gin.H{"message": "get cookie failed..."})fmt.Printf("err happened :%v\n", err)code := utils.GenInviteCode("cookie", 8)c.SetCookie("cookie", code, 3600*24*30, "/", "http://localhost:8090", false, false)}fmt.Println(cookieValue)c.Next()}
}

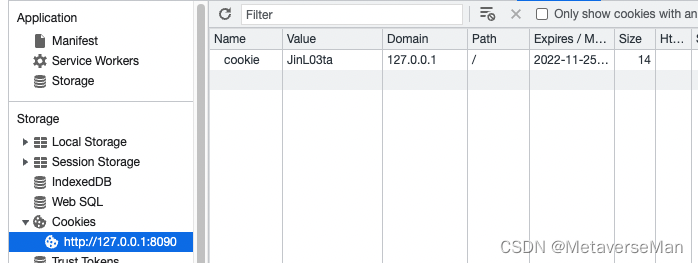
在这里插入图片描述

可以看到浏览器已经存下来了，再次刷新访问：

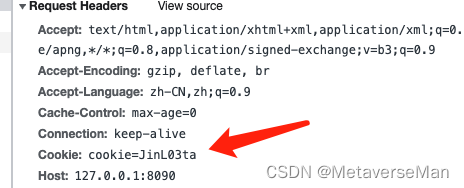
正常携带！
总结：
一：将domain设置正确，端口号一定要加上，协议可以不加。
二：（也是要在一的前提下）配置cookie Secure选项为ture，并配置samesite级别为：http.SameSiteNoneMode 或 4
三：（也是要在一的前提下）配置cookie Secure选项为ture，并没有配置samesite。我测试也是可以携带的

其实之前写java的时候 cookie session这些都研究过了。但是好久没复习，也没写记录。都已经还给时间了，所以解决问题的时候一定要记得做笔记📒 ！！！
ps:这次虽然没有手动在浏览器里进行任何设置，但是chrome cookie相关路径要知道：chrome://settings/cookies?search=cookie