1. 理论知识

我们需要关注那些按常理来说不太可能发生的事情。『信息量』就是用来度量事件的不确定性， 事件包含的信息量应与其发生的概率负相关 。假设$X$是一个离散型随机变量，它的取值集合为 { x 1 , x 2 , . . . , x n } \{x_{1},x_{2},...,x_{n}\} {x1​,x2​,...,xn​}，事件$X=x_i$的信息量为：
$$I(x_i)=-logP(X=x_i)$$

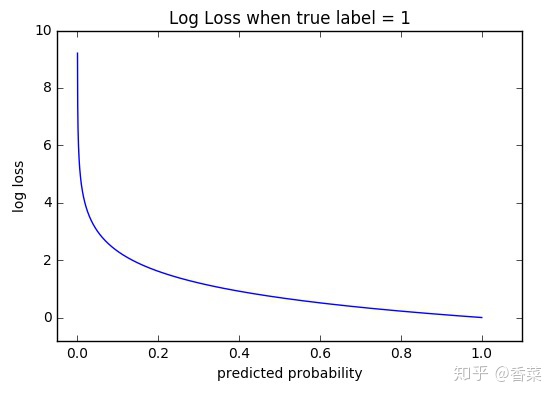
其中，$P$为变量$X$取值为$x_i$的概率，这个概率值应该落在0到1之间，则事件$X=x_i$的信息量的曲线图如下。当概率值$P$趋于0时，信息量趋于无穷大，概率值$P$等于1时，信息量为0。

---

进一步地，定义了『熵』来表示变量$X$整个概率分布的平均信息量 。随机变量$X$的熵的计算公式：

$$H(X)=-\sum _{i=1}^{n}P(X=x_i)logP(X=x_i)$$

《深度学习花书》中有一句结论：那些接近确定性的分布（输出几乎可以确定）具有较低的熵，那些接近均匀分布的概率分布具有较高的熵。即， 随机变量$X$的取值情况越随机，那么它的熵越高 。

---

用『相对熵（或叫KL散度）』来计算随机变量$X$的真实概率分布$P(X)$和与其近似的分布$Q(X)$两个的 差异 ：

$$D_{KL}(P||Q)=-\sum _{i=1}^{n}P(x_i)logQ(x_i)-(-\sum _{i=1}^{n}P(x_i)logP(x_i))=-\sum _{i=1}^{n}P(x_i)logQ(x_i)-H(P(X))$$

---

『交叉熵』$H(P,Q)$为：

$$H(P,Q)=H(P)+D_{KL}(P||Q)=-\sum _{i=1}^{n}P(x_i)logQ(x_i)$$

由于$P(X)$是真实概率分布，所以$H(P(X))$就是随机变量$X$的熵，那么 KL散度=交叉熵-熵 ，熵是已知的，求取 KL散度就等价于求交叉熵 ，所以交叉熵才会被用做神经网络训练中的损失函数。

2. 代码

Pytorch中使用交叉熵损失函数，直接调用nn.CrossEntropyLoss函数，使用一个例子来说明该函数的计算流程：

import torch.nn as nn
import torchloss = nn.CrossEntropyLoss()
input = torch.randn(2, 3, requires_grad=True)
target = torch.empty(2, dtype=torch.long).random_(3)
output = loss(input, target)# input
>>>tensor([[-0.0985,  1.6204, -0.5298],[-1.2966,  2.0098, -0.3128]])
# target
>>>tensor([1, 0])
# output
>>>tensor(1.8459)

用通俗点的方法来说明下计算流程

input为模型输出的概率分布，nn.CrossEntropyLoss函数内嵌了nn.softmax

• 第一步：input先进行softmax操作

softmax = nn.Softmax()
input_softmax = softmax(input)
# input_softmax
>>>tensor([[0.1383, 0.7718, 0.0899],[0.0323, 0.8813, 0.0864]])

• 第二步：以概率分布的形式表示target

# target
>>>tensor([[0, 1, 0],[1, 0, 0]])

该例子中minibatch=2，可以看作包含了两个随机变量$X_1$和$X_2$，那么input_softmax为这两个变量的预测分布[$Q_1$, $Q_2$]，target为两个变量的真实分布[$P_1$, $P_2$]

• 第三步：分别计算$X_1$和$X_2$的交叉熵

$$H(P_1,Q_1)=-\sum _{i=1}^3{P}_1(x_i)log{Q}_1(x_i)=-(0\ast log(0.1383)+1\ast log(0.7718)+0\ast log(0.0899))=0.2591$$
$$H(P_2,Q_2)=-\sum _{i=1}^3{P}_2(x_i)log{Q}_2(x_i)=-(1\ast log(0.0323)+0\ast log(0.8813)+0\ast log(0.0864))=3.4328$$

• 第四步：计算这一个批次的损失

CLASS torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None,   			 							reduction='mean', label_smoothing=0.0)

其中reduction参数有两个选项，'mean'和'sum'（默认'mean'），也就是一个批次的损失是输出所有样本的交叉熵的平均值还是总和值。上面的例子是用的默认值，所以最终的输出的
$$output=\frac{H(P_1,Q_1)+H(P_2,Q_2)}{2}=\frac{0.2591+3.4328}{2}=1.8459$$

---

【Tips】：torch从1.10.0版本开始支持两种target形式，除了上面Example of target with class indices，还有Example of target with class probabilities：

input = torch.randn(2, 3, requires_grad=True)
target = torch.randn(2, 3).softmax(dim=1)
output = loss(input, target)

---

参考：交叉熵损失函数（Cross Entropy Loss）