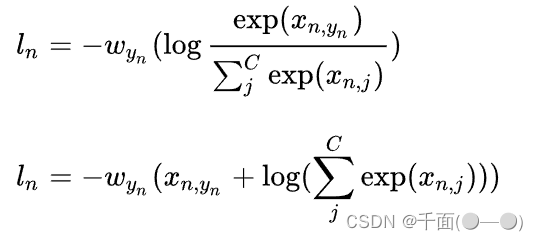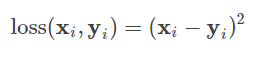0、前景介绍
对于线性回归模型适用于输出为连续值的情景,但是在模型输出是一个像图像类别这样的离散值时。对于这样离散值的预测问题,通常使用一些例如sigmoid/softmax的分类模型。
1. 图像分类任务
假设下面两个模型都是通过softmax的方式得到对于每个预测结果的概率值:
模型1:
| 预测 | 真实 | 是否正确 |
|---|---|---|
| 0.3 0.3 0.4 | 0 0 1 (猪) | 正确 |
| 0.3 0.4 0.3 | 0 1 0 (狗) | 正确 |
| 0.1 0.2 0.7 | 1 0 0 (猫) | 错误 |
模型1对于样本1和样本2以非常微弱的优势判断正确,对于样本3的判断则彻底错误。
模型2:
| 预测 | 真实 | 是否正确 |
|---|---|---|
| 0.1 0.2 0.7 | 0 0 1 (猪) | 正确 |
| 0.1 0.7 0.2 | 0 1 0 (狗) | 正确 |
| 0.3 0.4 0.3 | 1 0 0 (猫) | 错误 |
模型2对于样本1和样本2判断非常准确,对于样本3判断错误,但是相对来说没有错得太离谱。
1.1 分类错误率
最为直接的损失函数定义为:
ErrorNumm:预测错误数 AllNum:总预测数
模型1:
模型2:
可以看出,模型1和模型2的分类预测结果一样,但是通过模型2可以看出,其预测错误项的误差相对较小,所以分类错误率对于这类情况表现得不是很好。
1.2 平方误差损失
平方误差损失其定义为:
为真实概率,
为期望概率,通常为0或1
求得模型1为:
同理可求得模型2为:
我们发现,MSE能够判断出来模型2优于模型1,那为什么不采样这种损失函数呢?主要原因是在分类问题中,使用sigmoid/softmx得到概率,配合MSE损失函数时,采用梯度下降法进行学习时,会出现模型一开始训练时,学习速率非常慢的情况(MSE损失函数)。
有了上面的直观分析,我们可以清楚的看到,对于分类问题的损失函数来说,分类错误率和均方误差损失都不是很好的损失函数,下面我们来看一下交叉熵损失函数的表现情况。
1.3 交叉熵损失函数
:标签,如果每个样本只有一个标签,则为0或1
:实际计算概率
其中带下标的是
中的非0即1的元素,在上式中,我们知道只有一个
为1,其余的都为0,所以上式可以写为:
假设训练数据集的样本数为n,交叉熵损失函数为:
同样的,如果每个样本只有一个标签,那么交叉熵损失函数可以简写为:
从另一个角度分析,我们可以知道最化等价于最大化
即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
现在我们利用这个表达式计算上面例子中的损失函数值:
模型1:
对所有样本的loss求平均:
模型2:
对所有样本的loss求平均:
2. 函数性质
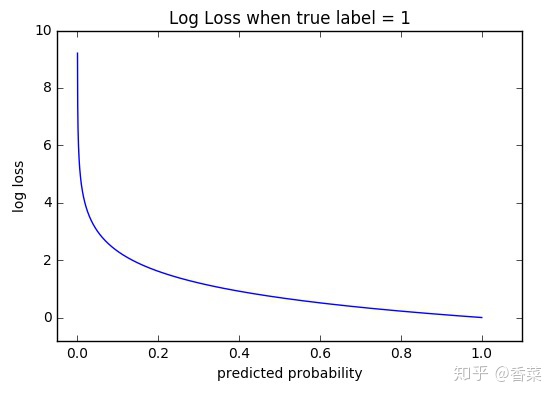
可以看出,该函数是凸函数,求导时能够得到全局最优值。
3. 学习过程
交叉熵损失函数经常用于分类问题中,特别是在神经网络做分类问题时,也经常使用交叉熵作为损失函数,此外,由于交叉熵涉及到计算每个类别的概率,所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。
我们用神经网络最后一层输出的情况,来看一眼整个模型预测、获得损失和学习的流程:
- 神经网络最后一层得到每个类别的得分scores(也叫logits);
- 该得分经过sigmoid(或softmax)函数获得概率输出;
- 模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。