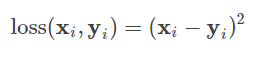我们知道，在二分类问题模型：例如逻辑回归「Logistic Regression」、神经网络「Neural Network」等，真实样本的标签为 [0，1]，分别表示负类和正类。模型的最后通常会经过一个 Sigmoid 函数，输出一个概率值，这个概率值反映了预测为正类的可能性：概率越大，可能性越大。

Sigmoid 函数的表达式和图形如下所示：

$g(s)=\frac{1}{1+e^{-s}}$

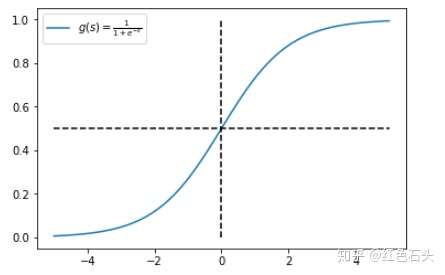
其中 s 是模型上一层的输出，Sigmoid 函数有这样的特点：s = 0 时，g(s) = 0.5；s >> 0 时， g ≈ 1，s << 0 时，g ≈ 0。显然，g(s) 将前一级的线性输出映射到 [0，1] 之间的数值概率上。这里的 g(s) 就是交叉熵公式中的模型预测输出。

我们说了，预测输出即 Sigmoid 函数的输出表征了当前样本标签为 1 的概率：

$\hat y=P(y=1|x)$

很明显，当前样本标签为 0 的概率就可以表达成：

$1-\hat y=P(y=0|x)$

重点来了，如果我们从极大似然性的角度出发，把上面两种情况整合到一起：

$P(y|x)=\hat y^y\cdot (1-\hat y)^{1-y}$

不懂极大似然估计也没关系。我们可以这么来看：

当真实样本标签 y = 0 时，上面式子第一项就为 1，概率等式转化为：

$P(y=0|x)=1-\hat y$

当真实样本标签 y = 1 时，上面式子第二项就为 1，概率等式转化为：

$P(y=1|x)=\hat y$

两种情况下概率表达式跟之前的完全一致，只不过我们把两种情况整合在一起了。

重点看一下整合之后的概率表达式，我们希望的是概率 P(y|x) 越大越好。首先，我们对 P(y|x) 引入 log 函数，因为 log 运算并不会影响函数本身的单调性。则有：

$log\ P(y|x)=log(\hat y^y\cdot (1-\hat y)^{1-y})=ylog\ \hat y+(1-y)log(1-\hat y)$

我们希望 log P(y|x) 越大越好，反过来，只要 log P(y|x) 的负值 -log P(y|x) 越小就行了。那我们就可以引入损失函数，且令 Loss = -log P(y|x)即可。则得到损失函数为：

$L=-[ylog\ \hat y+(1-y)log\ (1-\hat y)]$

非常简单，我们已经推导出了单个样本的损失函数，是如果是计算 N 个样本的总的损失函数，只要将 N 个 Loss 叠加起来就可以了：

$L=-\sum_{i=1}^Ny^{(i)}log\ \hat y^{(i)}+(1-y^{(i)})log\ (1-\hat y^{(i)})$

这样，我们已经完整地实现了交叉熵损失函数的推导过程。

2. 交叉熵损失函数的直观理解

可能会有读者说，我已经知道了交叉熵损失函数的推导过程。但是能不能从更直观的角度去理解这个表达式呢？而不是仅仅记住这个公式。好问题！接下来，我们从图形的角度，分析交叉熵函数，加深大家的理解。

首先，还是写出单个样本的交叉熵损失函数：

$L=-[ylog\ \hat y+(1-y)log\ (1-\hat y)]$

我们知道，当 y = 1 时：

$L=-log\ \hat y$

这时候，L 与预测输出的关系如下图所示：

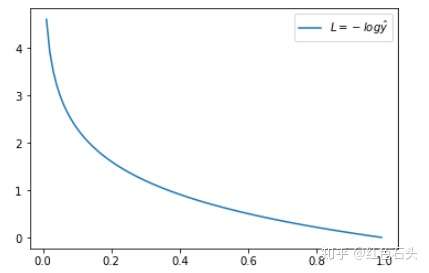
看了 L 的图形，简单明了！横坐标是预测输出，纵坐标是交叉熵损失函数 L。显然，预测输出越接近真实样本标签 1，损失函数 L 越小；预测输出越接近 0，L 越大。因此，函数的变化趋势完全符合实际需要的情况。

当 y = 0 时：

$L=-log\ (1-\hat y)$

这时候，L 与预测输出的关系如下图所示：

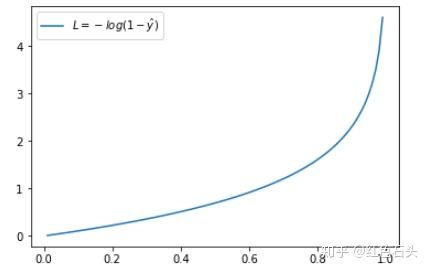
同样，预测输出越接近真实样本标签 0，损失函数 L 越小；预测函数越接近 1，L 越大。函数的变化趋势也完全符合实际需要的情况。

从上面两种图，可以帮助我们对交叉熵损失函数有更直观的理解。无论真实样本标签 y 是 0 还是 1，L 都表征了预测输出与 y 的差距。

另外，重点提一点的是，从图形中我们可以发现：预测输出与 y 差得越多，L 的值越大，也就是说对当前模型的 “ 惩罚 ” 越大，而且是非线性增大，是一种类似指数增长的级别。这是由 log 函数本身的特性所决定的。这样的好处是模型会倾向于让预测输出更接近真实样本标签 y。

3. 交叉熵损失函数的其它形式

什么？交叉熵损失函数还有其它形式？没错！我刚才介绍的是一个典型的形式。接下来我将从另一个角度推导新的交叉熵损失函数。

这种形式下假设真实样本的标签为 +1 和 -1，分别表示正类和负类。有个已知的知识点是Sigmoid 函数具有如下性质：

$1-g(s)=g(-s)$

这个性质我们先放在这，待会有用。

好了，我们之前说了 y = +1 时，下列等式成立：

$P(y=+1|x)=g(s)$

如果 y = -1 时，并引入 Sigmoid 函数的性质，下列等式成立：

$P(y=-1|x)=1-g(s)=g(-s)$

重点来了，因为 y 取值为 +1 或 -1，可以把 y 值带入，将上面两个式子整合到一起：

$P(y|x)=g(ys)$

这个比较好理解，分别令 y = +1 和 y = -1 就能得到上面两个式子。

接下来，同样引入 log 函数，得到：

$log\ P(y|x)=log\ g(ys)$

要让概率最大，反过来，只要其负数最小即可。那么就可以定义相应的损失函数为：

$L=-log g(ys)$

还记得 Sigmoid 函数的表达式吧？将 g(ys) 带入：

$L=-log\frac{1}{1+e^{-ys}}=log\ (1+e^{-ys})$

好咯，L 就是我要推导的交叉熵损失函数。如果是 N 个样本，其交叉熵损失函数为：

$L=\sum_{i=1}^Nlog\ (1+e^{-ys})$

接下来，我们从图形化直观角度来看。当 y = +1 时：

$L=log\ (1+e^{-s})$

这时候，L 与上一层得分函数 s 的关系如下图所示：

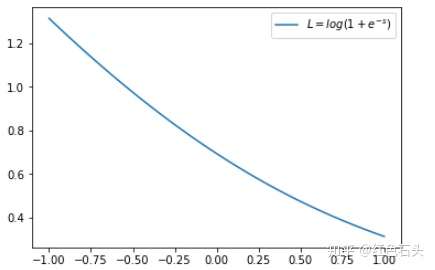
横坐标是 s，纵坐标是 L。显然，s 越接近真实样本标签 1，损失函数 L 越小；s 越接近 -1，L 越大。

另一方面，当 y = -1 时：

$L=log(1+e^s)$

这时候，L 与上一层得分函数 s 的关系如下图所示：

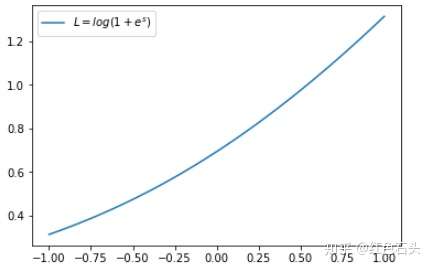
同样，s 越接近真实样本标签 -1，损失函数 L 越小；s 越接近 +1，L 越大。

4. 总结

本文主要介绍了交叉熵损失函数的数学原理和推导过程，也从不同角度介绍了交叉熵损失函数的两种形式。第一种形式在实际应用中更加常见，例如神经网络等复杂模型；第二种多用于简单的逻辑回归模型。

5.多分类交叉熵

交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。

交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。

单次观测下的多项式分布

$f_{multinomial}(x ; p) = \prod \limits _{i=1}^C p_i^{xi}$

其中，C代表类别数。p代表向量形式的模型参数，即各个类别的发生概率，如p=[0.1, 0.1, 0.7, 0.1]，则p1=0.1, p3=0.7等。即，多项式分布的模型参数就是各个类别的发生概率！x代表one-hot形式的观测值，如x=类别3，则x=[0, 0, 1, 0]。xi代表x的第i个元素，比如x=类别3时，x1=0，x2=0，x3=1，x4=0。

机器学习model对某个样本的输出，就代表各个类别发生的概率。但是，对于当前这一个样本而言，它肯定只能有一个类别，所以这一个样本就可以看成是一次实验（观察），而这次实验（观察）的结果要服从上述各个类别发生的概率，那不就是服从多项式分布嘛！而且是单次观察！各个类别发生的概率predict当然就是这个多项式分布的参数阿。

对于多类分类问题，似然函数就是衡量当前这个以predict为参数的单次观测下的多项式分布模型与样本值label之间的似然度。

所以，根据似然函数的定义，单个样本的似然函数即：

$L=f_{multinomial}(label ; predict)$