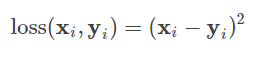交叉熵损失函数原理详解

之前在代码中经常看见交叉熵损失函数(CrossEntropy Loss)，只知道它是分类问题中经常使用的一种损失函数，对于其内部的原理总是模模糊糊，而且一般使用交叉熵作为损失函数时，在模型的输出层总会接一个softmax函数，至于为什么要怎么做也是不懂，所以专门花了一些时间打算从原理入手，搞懂它，故在此写一篇博客进行总结，以便以后翻阅。

交叉熵简介

交叉熵是信息论中的一个重要概念，主要用于度量两个概率分布间的差异性，要理解交叉熵，需要先了解下面几个概念。

信息量

信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。

“太阳从东边升起”，这条信息并没有减少不确定性，因为太阳肯定是从东边升起的，这是一句废话，信息量为0。

”2018年中国队成功进入世界杯“，从直觉上来看，这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大，而这句话消除了进入世界杯的不确定性，所以按照定义，这句话的信息量很大。

根据上述可总结如下：信息量的大小与信息发生的概率成反比。概率越大，信息量越小。概率越小，信息量越大。

设某一事件发生的概率为P(x)，其信息量表示为：
$$I\left(x\right)=-\log \left(P\left(x\right)\right)$$
其中$I\left(x\right)$表示信息量，这里$\log$表示以e为底的自然对数。

信息熵

信息熵也被称为熵，用来表示所有信息量的期望。

期望是试验中每次可能结果的概率乘以其结果的总和。

所以信息量的熵可表示为：（这里的$X$是一个离散型随机变量）
$$H\left(\mathbf{X}\right)=-\sum _{i=1}^{n}P(x_i)\log \left(P\left(x_i\right)))(\mathbf{X}=x_1,x_2,x_3...,x_n\right)$$
使用明天的天气概率来计算其信息熵：

序号	事件	概率P	信息量
1	明天是晴天	0.5	$-\log \left(0.5\right)$
2	明天出雨天	0.2	$-\log \left(0.2\right)$
3	多云	0.3	$-\log \left(0.3\right)$

$$H\left(\mathbf{X}\right)=-\left(0.5\ast \log \left(0.5\right)+0.2\ast \log \left(0.2\right)+0.3\ast \log \left(0.3\right)\right)$$

对于0-1分布的问题，由于其结果只用两种情况，是或不是，设某一件事情发生的概率为$P\left(x\right)$，则另一件事情发生的概率为$1-P\left(x\right)$，所以对于0-1分布的问题，计算熵的公式可以简化如下：
$$\begin{gathered} H\left(\mathbf{X}\right)=-\sum _{n=1}^{n}P(x_i\log \left(P\left(x_i\right))\right) \\ =-\left[P\left(x\right)\log \left(P\left(x\right)\right)+\left(1-P\left(x\right)\right)\log \left(1-P\left(x\right)\right)\right] \\ =-P\left(x\right)\log \left(P\left(x\right)\right)-\left(1-P\left(x\right)\right)\log \left(1-P\left(x\right)\right) \end{gathered}$$

相对熵（KL散度）

如果对于同一个随机变量$X$有两个单独的概率分布$P\left(x\right)$和$Q\left(x\right)$，则我们可以使用KL散度来衡量这两个概率分布之间的差异。

下面直接列出公式，再举例子加以说明。
$$D_{KL}\left(p||q\right)=\sum _{i=1}^{n}p\left(x_i\right)\log \left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right)$$
在机器学习中，常常使用$P\left(x\right)$来表示样本的真实分布，$Q\left(x\right)$来表示模型所预测的分布，比如在一个三分类任务中（例如，猫狗马分类器），$x_1,x_2,x_3$分别代表猫，狗，马，例如一张猫的图片真实分布$P\left(X\right)=[1,0,0]$, 预测分布$Q\left(X\right)=[0.7,0.2,0.1]$，计算KL散度：
$$\begin{gathered} D_{KL}\left(p||q\right)=\sum _{i=1}^{n}p\left(x_i\right)\log \left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right) \\ =p\left(x_1\right)\log \left(\frac{p\left(x_1\right)}{q\left(x_1\right)}\right)+p\left(x_2\right)\log \left(\frac{p\left(x_2\right)}{q\left(x_2\right)}\right)+p\left(x_3\right)\log \left(\frac{p\left(x_3\right)}{q\left(x_3\right)}\right) \\ =1\ast \log \left(\frac{1}{0.7}\right)=0.36 \end{gathered}$$
KL散度越小，表示$P\left(x\right)$与$Q\left(x\right)$的分布更加接近，可以通过反复训练$Q\left(x\right)$来使$Q\left(x\right)$的分布逼近$P\left(x\right)$。

交叉熵

首先将KL散度公式拆开：
$$\begin{gathered} D_{KL}\left(p||q\right)=\sum _{i=1}^{n}p\left(x_i\right)\log \left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right) \\ =\sum _{i=1}^{n}p\left(x_i\right)log\left(p\left(x_i\right)\right)-\sum _{i=1}^{n}p\left(x_i\right)log\left(q\left(x_i\right)\right) \\ =-H\left(p\left(x\right)\right)+\left[-\sum _{i=1}^{n}p\left(x_i\right)log\left(q\left(x_i\right)\right)\right] \end{gathered}$$
前者$H\left(p\left(x\right)\right)$表示信息熵，后者即为交叉熵，KL散度 = 交叉熵 - 信息熵

交叉熵公式表示为：
$$H\left(p,q\right)=-\sum _{i=1}^{n}p\left(x_i\right)log\left(q\left(x_i\right)\right)$$
在机器学习训练网络时，输入数据与标签常常已经确定，那么真实概率分布$P\left(x\right)$也就确定下来了，所以信息熵在这里就是一个常量。由于KL散度的值表示真实概率分布$P\left(x\right)$与预测概率分布$Q\left(x\right)$之间的差异，值越小表示预测的结果越好，所以需要最小化KL散度，而交叉熵等于KL散度加上一个常量（信息熵），且公式相比KL散度更加容易计算，所以在机器学习中常常使用交叉熵损失函数来计算loss就行了。

交叉熵在单分类问题中的应用

在线性回归问题中，常常使用MSE(Mean Squared Error)作为loss函数，而在分类问题中常常使用交叉熵作为loss函数。

下面通过一个例子来说明如何计算交叉熵损失值。

假设我们输入一张狗的图片，标签与预测值如下：

*	猫	狗	马
Label	0	1	0
Pred	0.2	0.7	0.1

那么loss
$$loss=-\left(0\ast \log \left(0.2\right)+1\ast \log \left(0.7\right)+0\ast \log \left(0.1\right)\right)=0.36$$
一个batch的loss为
$$loss=-\frac{1}{m}\sum _{i=1}^m\sum _{j=1}^{n}p\left(x_{ij}\right)log\left(q\left(x_{ij}\right)\right)$$
其中m表示样本个数。

总结：

• 交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小，模型预测效果就越好。

• 交叉熵在分类问题中常常与softmax是标配，softmax将输出的结果进行处理，使其多个分类的预测值和为1，再通过交叉熵来计算损失。

参考：

https://blog.csdn.net/tsyccnh/article/details/79163834

THE END