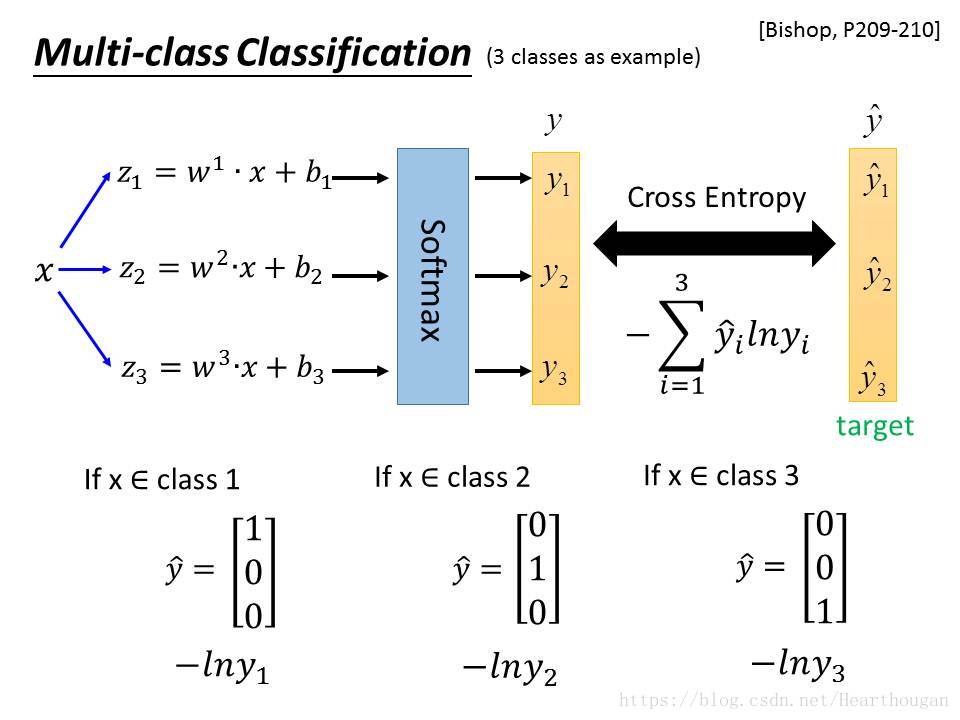
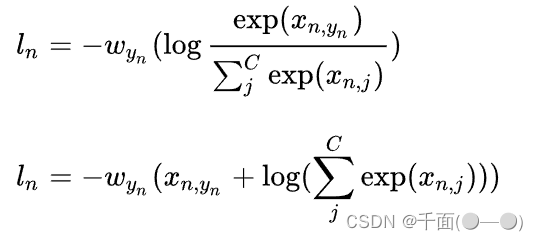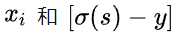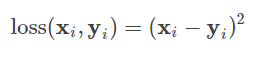图示Softmax及交叉熵损失函数

article/2025/9/10 3:49:38

Softmax函数

Softmax是将神经网络得到的多个值，进行归一化处理，使得到的值在 $[0,1]$ 之间，让结果变得可解释。即可以将结果看作是概率，某个类别概率越大，将样本归为该类别的可能性也就越高。Softmax就如下图（借鉴李宏毅老师的课件）

为了更加清晰的看清整个过程，我将其制作成gif，如下图所示：

交叉熵：

假设 $p$ 和 $q$ 是关于样本集的两个分布，其中 $p$ 是样本集的真实分布， $q$ 是样本集的估计分布，那么按照真是分布 $p$ 来衡量识别一个样本所需要编码长度的期望（即，平均编码长度）：

$H(p)=\sum_{i}^{n} p_{i}log\frac{1}{p_{i}}=\sum_{i}^{n}- p_{i}logp_{i}$

如果用估计分布 $q$ 来表示真实分布 $p$ 的平均编码长度，应为：

$H(p,q)=\sum_{i=1}^{n}p_{i}log\frac{1}{q_{i}}=\sum_{i=1}^{n}-p_{i}logq_{i}$

这是因为用 $q$ 来编码的样本来自于真是分布 $p$ ，所以期望值 $H(p,q)$ 中的概率是 $p_{i}$ 。而 $H(p,q)$ 就是交叉熵。

注:不了解什么是编码的请看这里：如何理解用信息熵来表示最短的平均编码长度。

在神经网络后面添加Softmax，真实的标签（或者是类别）就相当于真实的分布，经过Softmax得出的值就是预测的结果，因此可以使用交叉熵函数来作为损失函数。有了交叉熵的概念，我们就可以得出，Softmax的损失函数：

$L=\sum- \hat{y}_{i}lny_{i}$

其中 $y_{i}$ 是神经元的输出也可以作为预测结果， $\hat{y}_{i}$ 是第i个类别的真实值， $\hat{y}_{i}$ 只能取值 $0\: \: or\: \: 1$ 。在Softmax中我们取以 $e$ 为底的对数，因为都是 $e$ 的指数形式，可以方便计算。在反向传播的过程中，如何对交叉熵损失函数求导呢？可以先看下图的示例，显示了如何得到损失函数：

由上图可以看到，损失函数具体形式是什么。为了计算反向传播，我们从最后一层开始，也就是首先要对Softmax的输入 $z_{i}$ 求导，得：

$\frac{\partial L}{\partial z_{i}}=\frac{\partial L}{\partial y_{j}}\frac{\partial y_{j}}{\partial z_{i}}$ ，其中 $\left\{\begin{matrix} \begin{matrix} y_{j}=\frac{e^{z_{j}}}{\sum_{k}e^{z_{k}}}\\ \\ \, \, \, \, \, \, \, \, \, L=-\sum_{j}\hat{y_{j}}lny_{j}\\ \end{matrix} \end{matrix}\right.$

由于每个 $y_{j}$ 的分母中都有 $z_{i}$ 的贡献，故我们要考虑每一个输出值。则：

$\frac{\partial L}{\partial y_{j}}=\frac{\partial[ -\sum_{j}\hat{y_{j}}logy_{j}]}{\partial y_{j}}=-\sum_{j}\frac{\hat{y_{j}}}{y_{j}}$

对于 $\frac{\partial y_{j}}{\partial z_{i}}$ ，需要分开讨论因为 $j=i$ 和 $j\neq i$ 时的求导结果不同，故需分开讨论。则

$\frac{\partial L}{\partial z_{i}}=\sum_{j}\frac{\partial (-\hat{y}_{j}lny_{j})}{\partial z_{i}} =\sum_{j}\frac{\partial (-\hat{y}_{j}lny_{j})}{\partial y_{j}} \frac{\partial (y_{j})}{\partial z_{i}}=\left\{\begin{matrix} \frac{\partial (-\hat{y}_{i}lny_{i})}{\partial y_{i}} \frac{ \partial (\frac{e^{z_{i}}}{\sum_{k}e^{z_{k}}})}{\partial z_{i}}&j=i \\ & \\ \sum_{j\neq i}\frac{\partial (-\hat{y}_{j}lny_{j})}{\partial y_{j}} \frac{ \partial (\frac{e^{z_{j}}}{\sum_{k}e^{z_{k}}})}{\partial z_{i}}&j\neq i \end{matrix}\right.$

当 $j=i$ 时，有：

$\large {\color{Magenta} \begin{matrix} {\color{Golden} \frac{\partial y_{j}}{\partial z_{i}}}=\frac{\partial y_{i}}{\partial z_{i}}=\frac{\partial [\frac{e^{z_{i}} }{\sum_{k}e^{z_{k}}}]}{\partial z_{i}}=\frac{e^{z_{i}}\sum_{k}e^{z_{k}}-(e^{z_{i}})^{2} }{ (\sum_{k}e^{z_{k}})^{2} }\\ \\ \: \: \: \: =\frac{e^{z_{i}} }{\sum_{k}e^{z_{k}} }(1-\frac{e^{z_{i}} }{\sum_{k}e^{z_{k}} })=y_{i}(1-y_{i}) \end{matrix}}$

当 $j\neq i$ 时

${\color{Magenta} {\color{Golden} \frac{\partial y_{j}}{\partial z_{i}}}=\frac{\partial [\frac{e^{z_{j}} }{\sum_{k}e^{z_{k}}}]}{\partial z_{i}}=\frac{0-e^{z_{j}}e^{z_{i}} }{ (\sum_{k}e^{z_{k}})^{2} }=-y_{i}y_{j}}$

故，

$\large \begin{matrix} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,\, {\color{Red} \frac{\partial L}{\partial z_{i}}}=-\sum_{j}\frac{\hat{y_{j}}}{y_{j}}\frac{\partial y_{j}}{\partial z_{i}}\\ \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: =-\frac{\hat{y_{i}}}{y_{i}}y_{i}(1-y_{i})+\sum_{j\neq i}\frac{\hat{y_{j}}}{y_{j}}y_{i}y_{j}\\ \\ \: \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \: \: \: \: \: \: \: \: \: \: \: =y_{i}\hat{y}_{i}-\hat{y}_{i}+\sum_{j\neq i}y_{i}\hat{y}_{j}\\ \\ \: \: \: \: \: \: \: \: \:\: \: \: \: \: \: \: \: \: \: \: \: =-\hat{y}_{i}+\sum_{j}y_{i}\hat{y}_{j}\\ \\ \; \; \; \; \; \; \;\: \: \: \: \: \: \: \: \: \: \: \: \: =-\hat{y}_{i}+y_{i}\sum_{j}\hat{y}_{j}\\ \\ \: \: \: \: \: \: ={\color{Magenta} y_{i}-\hat{y_{i}}} \end{matrix}$

注：因为如果给定一个样本 $\large x$ 那么他对应的真实标签只有一个值为 $\large 1$ ，其余为0，故，

$\sum_{j}\hat{y}_{j}=1$

Sotfmax的交叉熵损失函数，还有另外的形式：

$L_{i} = - \sum_{j=1}^{k} 1\left\{y_{(i)} = j\right\} \log \frac{e^{z_{j}}}{\sum_{l=1}^k e^{z_{k} }}=-\hat{y}_{i}lny_{i}$
$\begin{matrix} L = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y_{(i)} = j\right\} \log \frac{e^{z_{j}}}{\sum_{l=1}^k e^{z_{k} }}\right]\\ \\ \; \; \; \; \; \; \; \; \; \; \; \; =- \frac{1}{m} \left[ \sum_{i=1}^{m} \hat{y}_{i} \log \frac{e^{z_{i}}}{\sum_{l=1}^k e^{z_{k} }}\right] {\color{Magenta} =- \frac{1}{m} \left[ \sum_{i=1}^{m} \hat{y}_{i} \log y_{i}\right]} \end{matrix}$