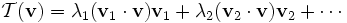这次给大家带来PHP实现多元线性回归模拟曲线算法步骤详解,PHP实现多元线性回归模拟曲线算法的注意事项有哪些,下面就是实战案例,一起来看一下。
多元线性回归模型: y = b1x1 + b2x2 + b3x3 +...... +bnxn;
我们根据一组数据: 类似 arr_x = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]]; arr_y = [5, 10, 15]; 我们最后要求出的是一个数组,包含了从b1 到bn;
方法:利用最小二乘法
公式:
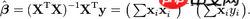 我们只用公式的前半部分,也就是用矩阵来计算
我们只用公式的前半部分,也就是用矩阵来计算
式中的X就是arr_x,二维数组我们可以把它看成是一个矩阵,式中的y就是arr_y,也把它看成一个矩阵(5, 10, 15) ,不过应该是竖着写的。
然后可以根据公式我们会发现要用到矩阵的相乘,转置,求逆;所以下面的代码一一给出:public function get_complement($data, $i, $j) {
/* x和y为矩阵data的行数和列数 */
$x = count($data);
$y = count($data[0]);
/* data2为所求剩余矩阵 */
$data2 =[];
for ($k = 0; $k < $x -1; $k++) {
if ($k < $i) {
for ($kk = 0; $kk < $y -1; $kk++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k][$kk];
} else {
$data2[$k][$kk] = $data[$k][$kk +1];
}
}
} else {
for ($kk = 0; $kk < $y -1; $kk++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k +1][$kk];
} else {
$data2[$k][$kk] = $data[$k +1][$kk +1];
}
}
}
}
return $data2;
}
/* 计算矩阵行列式 */
public function cal_det($data) {
$ans = 0;
if (count($data[0]) === 2) {
$ans = $data[0][0] * $data[1][1] - $data[0][1] * $data[1][0];
} else {
for ($i = 0; $i < count($data[0]); $i++) {
$data_temp = $this->get_complement($data, 0, $i);
if ($i % 2 === 0) {
$ans = $ans + $data[0][$i] * ($this->cal_det($data_temp));
} else {
$ans = $ans - $data[0][$i] * ($this->cal_det($data_temp));
}
}
}
return $ans;
}
/*计算矩阵的伴随矩阵*/
public function ajoint($data) {
$m = count($data);
$n = count($data[0]);
$data2 =[];
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
if (($i + $j) % 2 === 0) {
$data2[$i][$j] = $this->cal_det($this->get_complement($data, $i, $j));
} else {
$data2[$i][$j] = - $this->cal_det($this->get_complement($data, $i, $j));
}
}
}
return $this->trans($data2);
}
/*转置矩阵*/
public function trans($data) {
$i = count($data);
$j = count($data[0]);
$data2 =[];
for ($k2 = 0; $k2 < $j; $k2++) {
for ($k1 = 0; $k1 < $i; $k1++) {
$data2[$k2][$k1] = $data[$k1][$k2];
}
}
/*将矩阵转置便可得到伴随矩阵*/
return $data2;
}
/*求矩阵的逆,输入参数为原矩阵*/
public function inv($data) {
$m = count($data);
$n = count($data[0]);
$data2 =[];
$det_val = $this->cal_det($data);
$data2 = $this->ajoint($data);
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
$data2[$i][$j] = $data2[$i][$j] / $det_val;
}
}
return $data2;
}
/*求两矩阵的乘积*/
public function getProduct($data1, $data2) {
/*$data1 为左乘矩阵*/
$m1 = count($data1);
$n1 = count($data1[0]);
$m2 = count($data2);
$n2 = count($data2[0]);
$data_new =[];
if ($n1 !== $m2) {
return false;
} else {
for ($i = 0; $i <= $m1 -1; $i++) {
for ($k = 0; $k <= $n2 -1; $k++) {
$data_new[$i][$k] = 0;
for ($j = 0; $j <= $n1 -1; $j++) {
$data_new[$i][$k] += $data1[$i][$j] * $data2[$j][$k];
}
}
}
}
return $data_new;
}
/*多元线性方程*/
public function getParams($arr_x, $arr_y) {
$final =[];
$arr_x_t = $this->trans($arr_x);
$result = $this->getProduct($this->getProduct($this->inv($this->getProduct($arr_x_t, $arr_x)), $arr_x_t), $arr_y);
foreach ($result as $key => $val) {
foreach ($val as $_k => $_v) {
$final[] = $_v;
}
}
return $final;
}
最后的getParams()方法就是最后求b参数数组的方法,传入一个二维数组arr_x, 和一个一维数组arr_y就可以了。
相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!
推荐阅读: