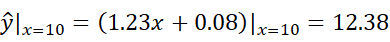🌠 『精品学习专栏导航帖』
- 🐳最适合入门的100个深度学习实战项目🐳
- 🐙【PyTorch深度学习项目实战100例目录】项目详解 + 数据集 + 完整源码🐙
- 🐶【机器学习入门项目10例目录】项目详解 + 数据集 + 完整源码🐶
- 🦜【机器学习项目实战10例目录】项目详解 + 数据集 + 完整源码🦜
- 🐌Java经典编程100例🐌
- 🦋Python经典编程100例🦋
- 🦄蓝桥杯历届真题题目+解析+代码+答案🦄
- 🐯【2023王道数据结构目录】课后算法设计题C、C++代码实现完整版大全🐯
文章目录
- 一、概述
- 二、最小二乘估计
2021人工智能领域新星创作者,带你从入门到精通,该博客每天更新,逐渐完善机器学习各个知识体系的文章,帮助大家更高效学习。

一、概述
在生活实际中经常遇到一些情况,比如根据公司内部一些人的工资待遇去预测一个将从事相同工作人的工资,我们需要根据已有数据来对未来的数据进行推测。
在高中时候我们学过最小二乘法就是求 a ∗ 和 b ∗ a^*和b^* a∗和b∗ 去拟合一条直线,来最大程度的是我们的样本点落在该直线上。
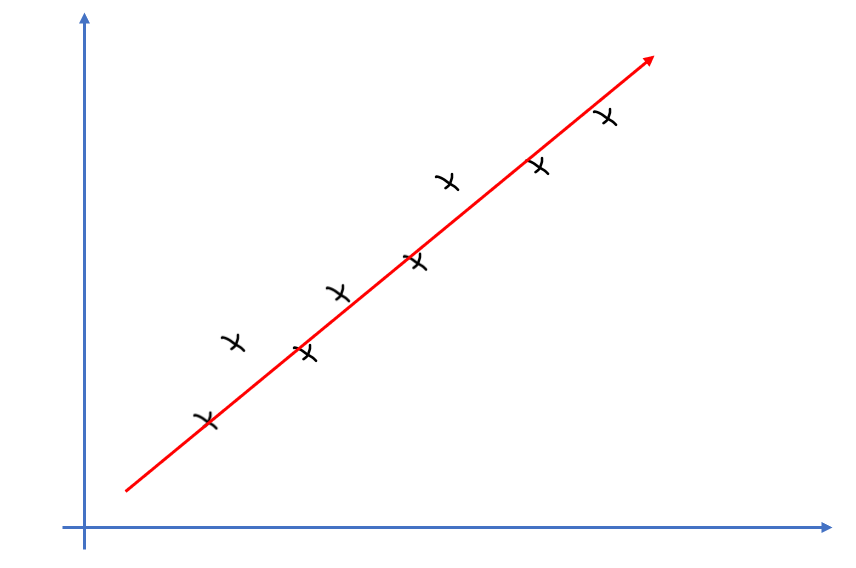
由上图,显然我们希望的是找到一条直线使所以的样本点尽可能靠近该直线,即每个样本点到直线的距离最短,其实这么说还不太对,它不是到直线的距离最短,而是到与该样本点相同x点的y值的距离最短,如果是到直线的距离最短没有几何意义,如果是竖直距离,它可以表示我们预测值和真实值之间的一种离散程度,显然这个差值越小越好。
二、最小二乘估计
根据上面的理解这就引出了我们的损失函数,也就是最小二乘估计:
在给出公式之前,我们先给出一些约定,为了下面叙述方便:
- x i x_i xi:每个样本为列向量,形状为(n,1)
- X:样本矩阵,为(m,n)
注意:
X = [ x 1 T x 2 T . . . x m T ] = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋱ ⋮ x m 1 x m 2 ⋯ x m n ] X=\begin{bmatrix}x_1^T\\x_2^T\\...\\x_m^T\end{bmatrix}\\=\begin{bmatrix}{x_{11}}&{x_{12}}&{\cdots}&{x_{1n}}\\{x_{21}}&{x_{22}}&{\cdots}&{x_{2n}}\\{\vdots}&{\vdots}&{\ddots}&{\vdots}\\{x_{m1}}&{x_{m2}}&{\cdots}&{x_{mn}}\\\end{bmatrix} X=⎣⎢⎢⎡x1Tx2T...xmT⎦⎥⎥⎤=⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1nx2n⋮xmn⎦⎥⎥⎥⎤
- w:为列向量,形状为(n,1)
我们下面公式推导的时候没有b,只是用了 y = X W y=XW y=XW ,这只是为了方便,其实可以把b放在X中和W向量中一起计算也可以,这样就变成了:
X = [ x 11 x 12 ⋯ x 1 n 1 x 21 x 22 ⋯ x 2 n 1 ⋮ ⋮ ⋱ ⋮ x m 1 x m 2 ⋯ x m n 1 ] X=\begin{bmatrix}{x_{11}}&{x_{12}}&{\cdots}&{x_{1n}}&1\\{x_{21}}&{x_{22}}&{\cdots}&{x_{2n}}&1\\{\vdots}&{\vdots}&{\ddots}&{\vdots}\\{x_{m1}}&{x_{m2}}&{\cdots}&{x_{mn}}&1\\\end{bmatrix} X=⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1nx2n⋮xmn111⎦⎥⎥⎥⎤
W = [ w 1 w 2 ⋮ w n w 0 ] W=\begin{bmatrix}w_1\\w_2\\\vdots\\w_n\\w0\end{bmatrix} W=⎣⎢⎢⎢⎢⎢⎡w1w2⋮wnw0⎦⎥⎥⎥⎥⎥⎤
如果把两个矩阵这样写,其实是和 X W + b = Y XW+b=Y XW+b=Y 是等价的。
L ( w ) = ∑ i = 1 m ∣ ∣ w T x i − y i ∣ ∣ 2 = ∑ i = 1 m ( w T x i − y i ) 2 = [ w T x 1 − y 1 w T x 2 − y 2 . . . w T x m − y m ] [ w T x 1 − y 1 w T x 2 − y 2 . . . w T x m − y m ] = [ W T X T − Y T ] [ X W − Y ] = W T X T X W − Y T X W − W T X T Y + Y T Y = W T X T X W − 2 W T X T Y + Y T Y L(w)=\sum_{i=1}^m||w^Tx_i-y_i||^2\\=\sum_{i=1}^m(w^Tx_i-y_i)^2\\=\begin{bmatrix}w^Tx_1-y_1&&w^Tx_2-y_2&&...&&w^Tx_m-y_m\end{bmatrix}\begin{bmatrix}w^Tx_1-y_1\\w^Tx_2-y_2\\...\\w^Tx_m-y_m\end{bmatrix}\\=[W^TX^T-Y^T][XW-Y]\\=W^TX^TXW-Y^TXW-W^TX^TY+Y^TY\\=W^TX^TXW-2W^TX^TY+Y^TY L(w)=i=1∑m∣∣wTxi−yi∣∣2=i=1∑m(wTxi−yi)2=[wTx1−y1wTx2−y2...wTxm−ym]⎣⎢⎢⎡wTx1−y1wTx2−y2...wTxm−ym⎦⎥⎥⎤=[WTXT−YT][XW−Y]=WTXTXW−YTXW−WTXTY+YTY=WTXTXW−2WTXTY+YTY
因为我们采用的是最小二乘估计,所以我们希望我们的损失函数最小,所以我们求取函数导数为0的点,就是我们的最优解,有人可能有疑问,导数为0的点不一定是最值点,这里说明一下,因为我们的损失函数为凸函数,有因为凸函数是可优化的,所以该函数导数为0的点一定是最值点。
你可以想象二次函数 y = x 2 y=x^2 y=x2 ,他就是一个凸函数,显然它的导数为0的点一定是我们的最小值点,这里的损失函数为什么是最小值不予证明。
所以我们的最优解就为:
w ∗ = a r g m i n w L ( w ) w^*=argmin_wL(w) w∗=argminwL(w)
此时就需要对函数进行求导,令其导数为0
∂ L ( w ) ∂ w = 2 X T X W − 2 X T Y = 0 \frac{\partial L(w)}{\partial w}=2X^TXW-2X^TY=0 ∂w∂L(w)=2XTXW−2XTY=0
这里可能有人不会进行矩阵求导,我来讲两种方式,第一种就是损失函数不采用矩阵方式进行表达,用求和符号将其变成每个样本的损失然后求和,针对于每个样本对其求导,然后讲每个样本的导数相加,这样就避免了矩阵的求导。
我采用的是第二种方式:
我们讲原矩阵写成微分的形式:
d L ( w ) = t r ( ∂ L ∂ w T d ( w ) ) = d ( W T X T X W − Y T X W − W T X T Y + Y T Y = W T X T X W − 2 W T X T Y + Y T Y ) = d ( W T ) X T X W + W T X T X d ( W ) − 2 d ( W T ) X T Y = X T X W d ( W T ) + W T X T X d ( W ) − 2 X T Y d ( W T ) dL(w)=tr(\frac{\partial L}{\partial w}^Td(w))=d(W^TX^TXW-Y^TXW-W^TX^TY+Y^TY\\=W^TX^TXW-2W^TX^TY+Y^TY)\\=d(W^T)X^TXW+W^TX^TXd(W)-2d(W^T)X^TY\\=X^TXWd(W^T)+W^TX^TXd(W)-2X^TYd(W^T) dL(w)=tr(∂w∂LTd(w))=d(WTXTXW−YTXW−WTXTY+YTY=WTXTXW−2WTXTY+YTY)=d(WT)XTXW+WTXTXd(W)−2d(WT)XTY=XTXWd(WT)+WTXTXd(W)−2XTYd(WT)
所以
∂ L ( w ) ∂ w = 2 X T X W − 2 X T Y = 0 \frac{\partial L(w)}{\partial w}=2X^TXW-2X^TY=0 ∂w∂L(w)=2XTXW−2XTY=0
这样我们就求出了最优解w:
w ∗ = ( X T X ) − 1 X T Y w^*=(X^TX)^{-1}X^TY w∗=(XTX)−1XTY
然后我们就可以构造决策函数:
f ( x ) = ( w ∗ ) T x f(x)=(w^*)^Tx f(x)=(w∗)Tx
使用该函数就可以拟合我们的每一个样本点。
写在最后
大家好,我是阿光,觉得文章还不错的话,记得“一键三连”哦!!!