堆排序介绍
堆排序(Heap Sort)就来利用堆(假设利用大顶堆)进行排序的方法。它的基本思想是,将待排序的序列构成一个大顶堆。此时,整个序列的最大值就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次小值。如何反复执行,便能得到一个有序序列了。
定义看懂没有?没看懂没关系,下面看图解。
堆排序图解
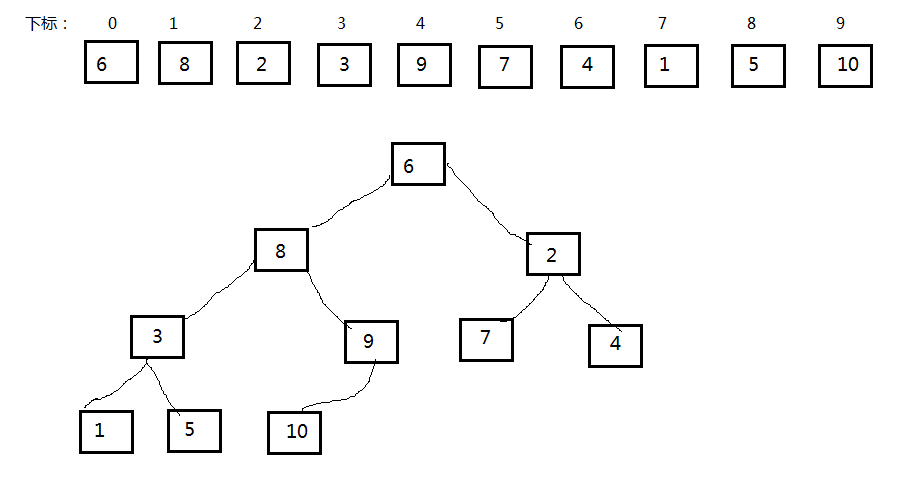
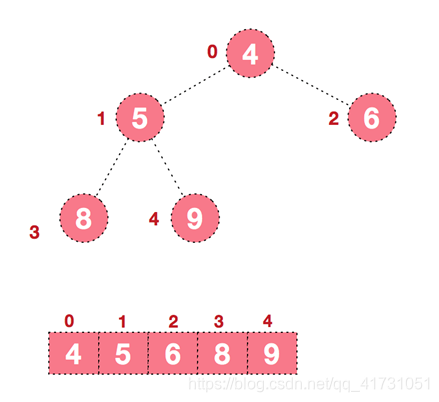
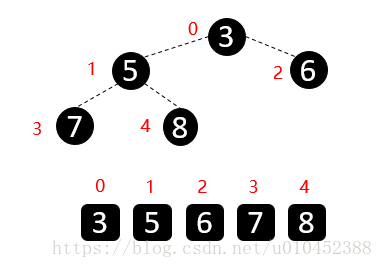
我们先来说说堆,我们这来看大顶堆,说大顶堆前,我先看 一个数组如何模拟成树的。请看下图,将数组元素从下标0开始,看做完全二叉树结点,请以层序遍历的角度看待它。
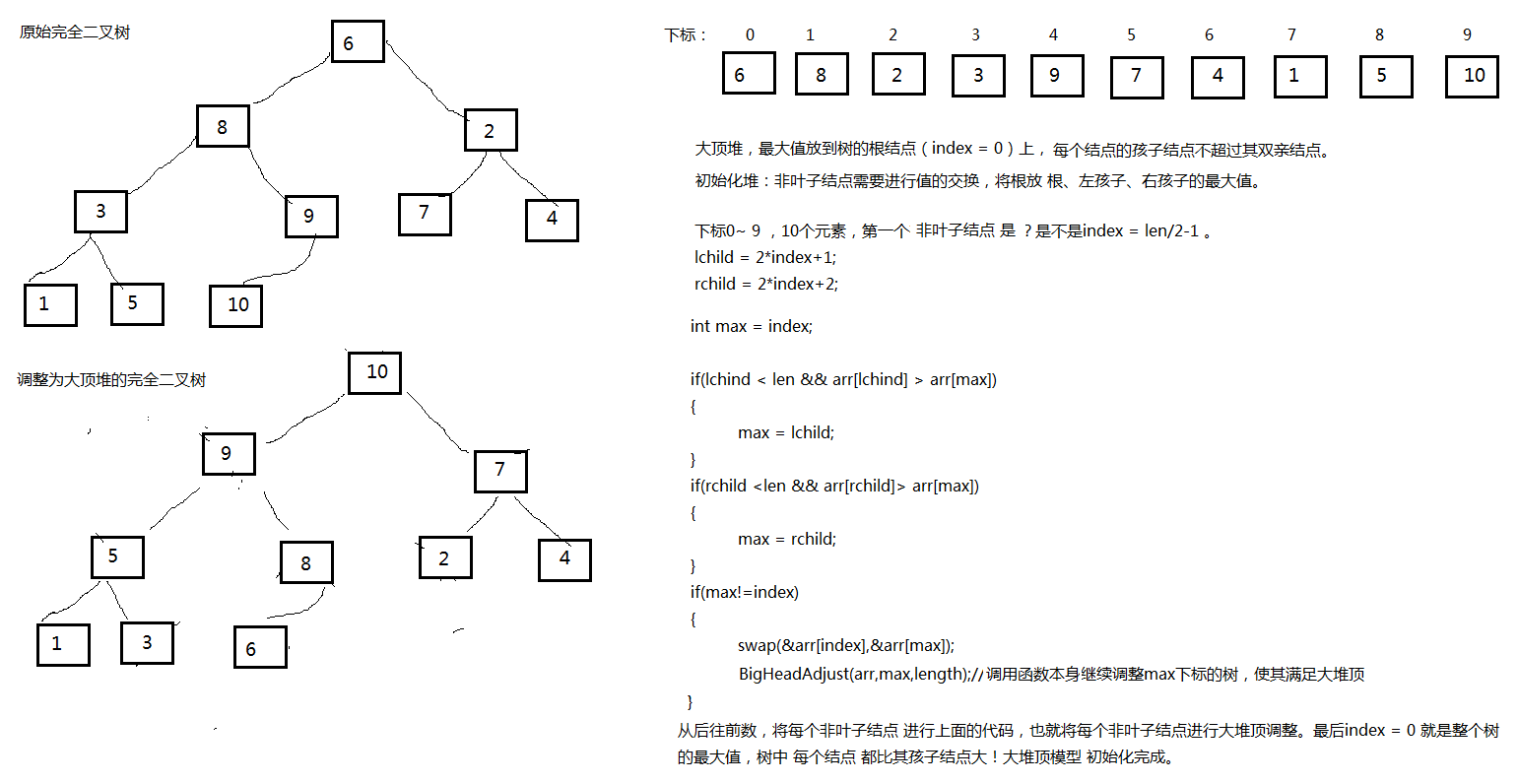
我先来构造大顶堆,在构造堆之前,我们先看下堆的定义,堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。我们从后往前将每个结点构成一个大顶堆不就得了?想想不是呢?因为最下层的结点已经满足堆条件,然后调整上层结点,使其满足大顶堆条件,那么整个完全二叉树不就成了大顶堆了么。我们应该从后面的那个结点开始呢?当然是从非叶子结点 9 开始呀,因为叶子结点没有孩子结点呗。将结点9看做一棵树将其调整问堆,然后将3位根结点的树调整为堆,然后将2为根结点的树调整为堆........,整棵完全二叉树就调整好了,成为了一个大顶堆。请看下图的代码和说明。
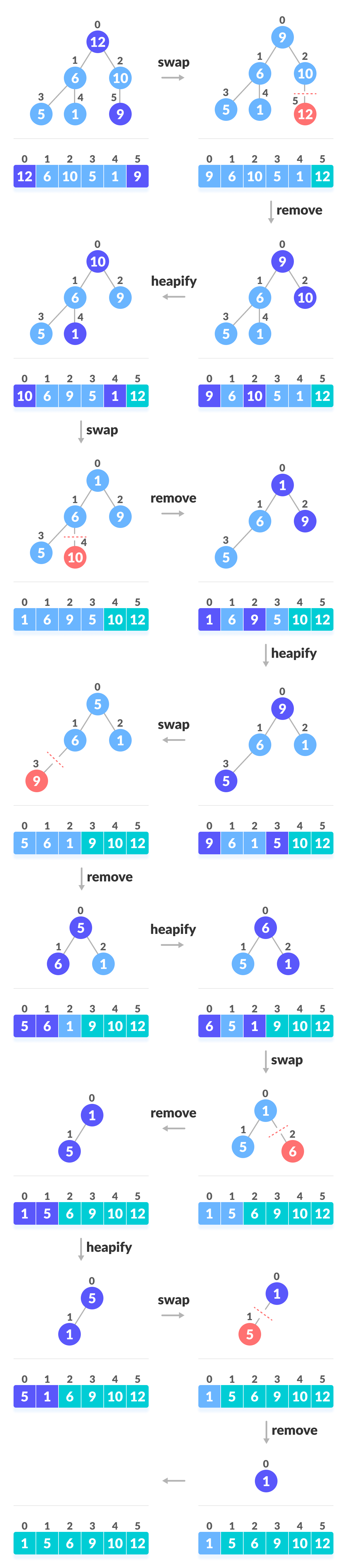
将堆的初始化看懂了,就已经成功了一大半了。还有一小部分就是 将最值(下标为0)放到序列的尾部,然后将剩下的元素继续进行堆调整,堆顶(下标为0)的元素 又是次最值,将其放到尾部,这样一直循环 直到将每个元素放到堆顶,则堆排序完毕。
堆排序代码
下面请堆排序代码,然后再进行解说。
//堆调整 大堆顶,将最大值放在根结点
void BigHeadAdjust(int *arr,int index,int length)
{int lchild = 2 * index + 1;int rchild = 2 * index + 2;int max = index;if (lchild<length&&arr[lchild]>arr[max]){max = lchild;}if (rchild<length&&arr[rchild]>arr[max]){max = rchild;}if (max != index){Swap(&arr[max], &arr[index]);BigHeadAdjust(arr, max, length);}return;
}//堆排序,采用大顶堆 升序
void HeapSort_Up(int *arr, int length)
{//初始化堆,将每个非叶子结点倒叙进行大顶堆调整。//循环完毕 初始大顶堆(每个根结点都比它孩子结点值大)形成for (int i = length / 2 - 1; i >= 0; i--){BigHeadAdjust(arr, i, length);}printf("大堆顶初始化顺序:");PrintArr(arr, length);//将堆顶值放到数组尾部,然后又进行大堆顶调整,一次堆调整最值就到堆顶了。 for (int i = length - 1; i >= 0; i--){Swap(&arr[0], &arr[i]);BigHeadAdjust(arr, 0, i);}return;
}
细心的朋友,会发现初始化化堆 是从非叶子结点从后往前进行调整为堆,而后序的堆调整 都是从下标为0处开始调整为堆。因为起初的完全二叉树是完全无效的,所有只能从后往前调整。在初始化完堆之后,尽管将最值移动到尾部,打乱了堆,因为原来的堆结构已经基本形成,只需要递归调用BigHeadAdjust即可。
堆排序复杂度分析
堆排序,它的运行时间主要是消耗在构建堆和在重建堆时的反复筛选上。在构建堆的过程,因为我们是从完全二叉树最下层的非叶子结点开始构建的,将它与其孩子结点进行比较和有必要的互换,对于每个非叶子结点来说,其实最多2次比较和互换,故初始化堆的时间复杂度为O(n)。在正式排序的时候,第i次取堆顶记录和重建堆需要O(logi)的时间(完全二叉树的某个结点到根结点的距离为log2i+1),并且需要取n-1次堆顶记录,因此重建堆的时间复杂度为O(nlogn)。所以总的来说,堆排序的时间复杂度为O(nlogn)。由于堆排序对元素记录的排序状态不敏感,因此它无论最好,最坏,和平均时间复杂度均为O(nlogn)。
完整代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <sys/timeb.h>
#define MAXSIZE 1000000
//交换值
void Swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}
//打印数组元素
void PrintArr(int* arr, int length)
{for (int i = 0; i < length; i++){printf("%d ", arr[i]);}printf("\n");return;
}
long GetSysTime()
{struct timeb tb;ftime(&tb);return tb.time * 1000 + tb.millitm;
}//堆调整 大堆顶,将最大值放在根结点
void BigHeadAdjust(int *arr,int index,int length)
{int lchild = 2 * index + 1;int rchild = 2 * index + 2;int max = index;if (lchild<length&&arr[lchild]>arr[max]){max = lchild;}if (rchild<length&&arr[rchild]>arr[max]){max = rchild;}if (max != index){Swap(&arr[max], &arr[index]);BigHeadAdjust(arr, max, length);}return;
}//堆排序,采用大顶堆 升序
void HeapSort_Up(int *arr, int length)
{//初始化堆,将每个非叶子结点倒叙进行大顶堆调整。//循环完毕 初始大顶堆(每个根结点都比它孩子结点值大)形成for (int i = length / 2 - 1; i >= 0; i--){BigHeadAdjust(arr, i, length);}//printf("大堆顶初始化顺序:");//PrintArr(arr, length);//将堆顶值放到数组尾部,然后又进行大堆顶调整,一次堆调整最值就到堆顶了。 for (int i = length - 1; i >= 0; i--){Swap(&arr[0], &arr[i]);BigHeadAdjust(arr, 0, i);}return;
}//堆调整 小堆顶,将最小值放在根结点
void SmallHeadAdjust(int *arr, int index, int length)
{int lchild = 2 * index + 1;int rchild = 2 * index + 2;int min = index;if (lchild<length&&arr[lchild]<arr[min]){min = lchild;}if (rchild<length&&arr[rchild]<arr[min]){min = rchild;}if (min != index){Swap(&arr[min], &arr[index]);SmallHeadAdjust(arr, min, length);}return;
}//堆排序,采用小顶堆 降序
void HeapSort_Down(int *arr, int length)
{for (int i = length / 2 - 1; i >= 0; i--){SmallHeadAdjust(arr, i, length);}for (int i = length - 1; i >= 0; i--){Swap(&arr[0], &arr[i]);SmallHeadAdjust(arr, 0, i);}return;
}
//希尔排序 升序
//根据插入排序的原理,将原来的一个大组,采用间隔的形式分成很多小组,分别进行插入排序
//每一轮结束后 继续分成更小的组进行 插入排序,直到分成的小组长度为1,说明插入排序完毕
void ShellSort_Up(int* arr, int length)
{int increase = length;int i, j, k, temp;do{increase = increase / 3 + 1;//每个小组的长度//每个小组的第0个元素for (i = 0; i < increase; i++){//对每个小组进行插入排序,因为是间隔的形式分组,每个小组下一个元素为 j+=incresefor (j = i + increase; j < length; j += increase){temp = arr[j];//待插入元素for (k = j - increase; k >= 0 && temp < arr[k]; k -= increase){arr[k + increase] = arr[k];}arr[k + increase] = temp;}}} while (increase>1);
}int main(int argc, char *argv[])
{srand((size_t)time(NULL));//设置随机种子int arr[10] = { 6,8,2,3,9,7,4,1,5,10 };int *arr2 = (int*)malloc(sizeof(int)*MAXSIZE);int *arr3 = (int*)malloc(sizeof(int)*MAXSIZE);//给每个元素设置一个随机值for (int i = 0; i < MAXSIZE; i++){int num = rand() % MAXSIZE;arr2[i] = num;arr3[i] = num;}//printf("排序前:\n");//PrintArr(arr, 10);//printf("堆排序升序:\n");//HeapSort_Up(arr, 10);//PrintArr(arr, 10);//printf("堆排序降序:\n");//HeapSort_Down(arr, 10);//PrintArr(arr, 10);long start1 = GetSysTime();ShellSort_Up(arr2, MAXSIZE);long end1 = GetSysTime();printf("%d个元素 希尔排序耗费%d毫秒\n",MAXSIZE,end1-start1);long start2 = GetSysTime();HeapSort_Up(arr3, MAXSIZE);long end2 = GetSysTime();printf("%d个元素 堆排序耗费%d毫秒\n", MAXSIZE, end2 - start2);return 0;
}
运行结果检测
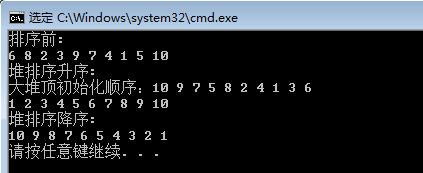
正确性验证
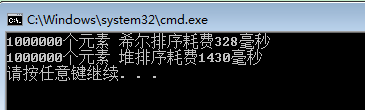
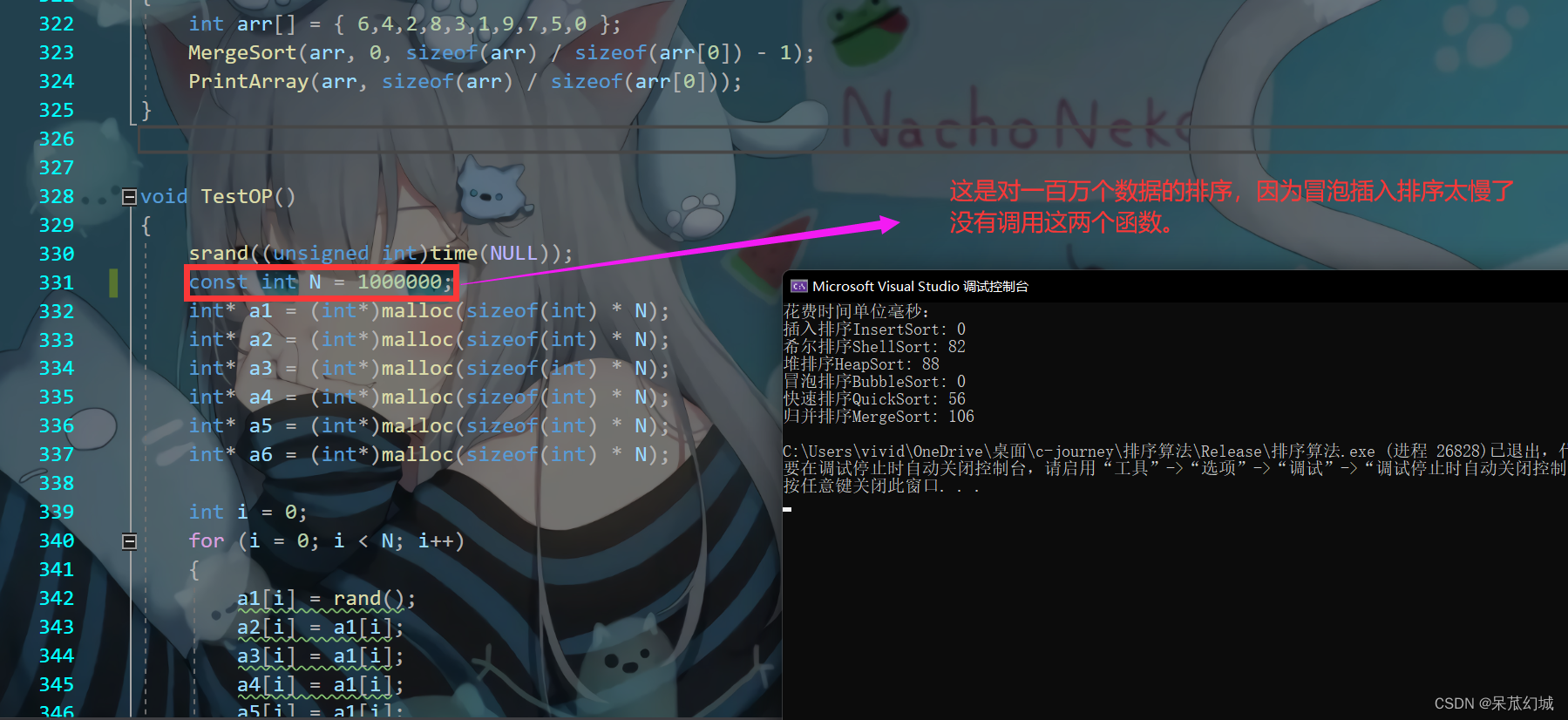
和希尔排序比较
排序100万个数据,比较下他们的效率。希尔排序居然比堆排序高,运行了好几遍都是这个结果。。。