堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

 基本思想

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

将待排序的序列构造成一个最大堆，此时序列的最大值为根节点 ，依次将根节点与待排序序列的最后一个元素交换，再维护从根节点到该元素的前一个节点为最大堆，如此往复，最终得到一个递增序列

假设给定一个组无序数列

创建最大堆

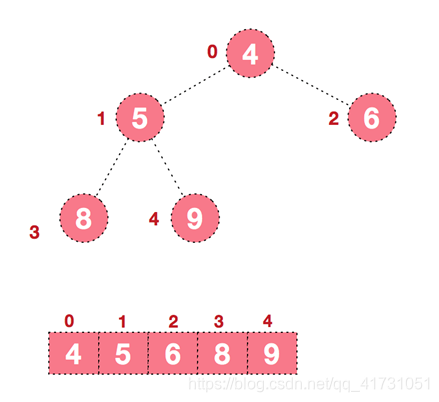
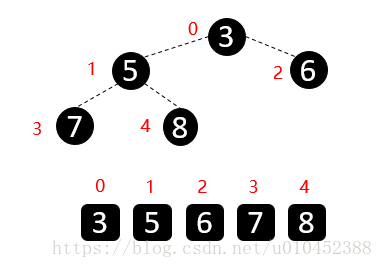
首先我们将数组我们将数组从上至下按顺序排列，转换成二叉树：一个无序堆。

 

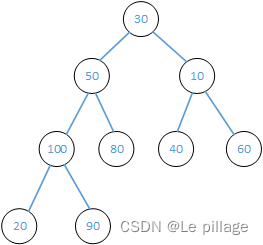
 从最后一个堆开始，即90那个堆开始；首先对比左右孩子，如果右孩子比左孩子的值大，交换左右孩子的值，然后比较左孩子与父节点的值，如果左孩子的值小于父节点的值，不用交换，如果发生交换，要检测子节点是否为其他堆的父节点，如果是，递归进行同样的操作。

然后的到最大堆

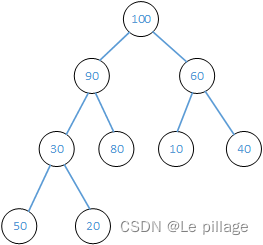
 堆排序（最大堆调整） 

将100与最底部的20交换位置，100变为有序区，之后将不再进入比较。

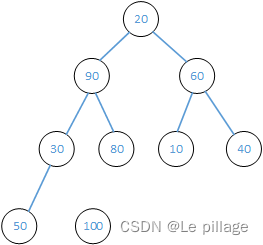
然后重新进行最大堆排序，20与下面的子节点比较，子节点最大的与20交换，然后进行递归操作。

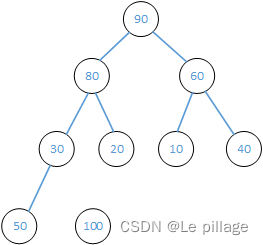
然后不断进行上述步骤，建立最大堆，并且扩大有序区，最终全部有序。

 

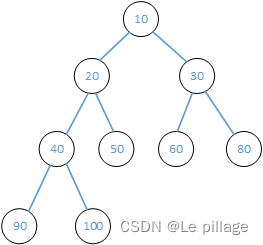
 代码实现

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
void swap(int* a, int* b) {int temp = *b;*b = *a;*a = temp;
}
void max_heapify(int arr[], int start, int end) {//建立父节点指标和子节点指标int dad = start;int son = dad * 2 + 1;while (son <= end) { //若子节点指标在范围内才做比较if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小，选择最大的son++;if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕，直接跳出函数return;else { //否则交换父子内容再继续子节点和孙节点比较swap(&arr[dad], &arr[son]);dad = son;son = dad * 2 + 1;}}
}
void heap_sort(int arr[], int len) {int i;//初始化，i从最后一个父节点开始调整for (i = len / 2 - 1; i >= 0; i--)max_heapify(arr, i, len - 1);//先将第一个元素和已排好元素前一位做交换，再从新调整，直到排序完毕for (i = len - 1; i > 0; i--) {swap(&arr[0], &arr[i]);max_heapify(arr, 0, i - 1);}
}
int main() 
{srand(time(NULL));int arr[9]={0};for(int j=0;j<9;j++){arr[j]=rand()%100;}int len = (int) sizeof(arr) / sizeof(*arr);heap_sort(arr, len);int i;for (i = 0; i < len; i++)printf("%4d ", arr[i]);printf("\n");return 0;
}

运行结果