一、堆排序算法原理和动态图解

       将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根节点。将它移走(其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次最大值。如此反复执行，就能得到一个有序序列了。这个过程其实就是先构建一个最大/最小二叉堆，然后不停的取出最大/最小元素（头结点），插入到新的队列中，以此达到排序的目的。如下图所示：

二、二叉树定义

        要了解堆首先得了解一下二叉树，在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。二叉树的每个结点至多只有二棵子树（不存在度大于 2 的结点），二叉树的子树有左右之分，次序不能颠倒。二叉树的第 i 层至多有 2i - 1 个结点；深度为 k 的二叉树至多有 2k - 1 个结点；对任何一棵二叉树 T，如果其终端结点数为 n0，度为 2 的结点数为 n2，则n0 = n2 + 1。二叉树又分为完全二叉树（complete binary tree）和满二叉树（full binary tree）。树和二叉树的三个主要差别：

• 树的结点个数至少为 1，而二叉树的结点个数可以为 0
• 树中结点的最大度数没有限制，而二叉树结点的最大度数为 2
• 树的结点无左、右之分，而二叉树的结点有左、右之分

1. 满二叉树：一棵深度为 k，且有 2k - 1 个节点称之为满二叉树，即每一层上的节点数都是最大节点数。如下图b所示：深度为3的满二叉树。
2. 完全二叉树：而在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树（Complete Binary Tree）。如下图a所示：是一个深度为4的完全二叉树。

三、堆的定义

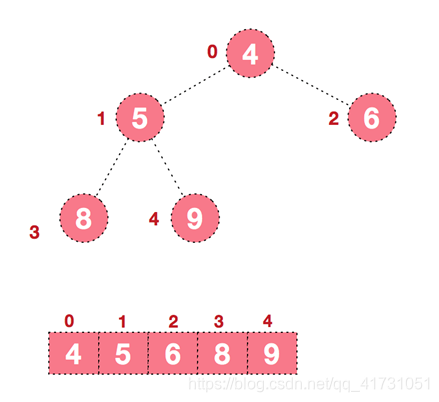
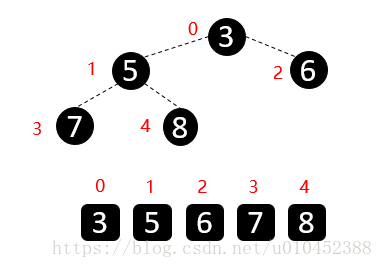
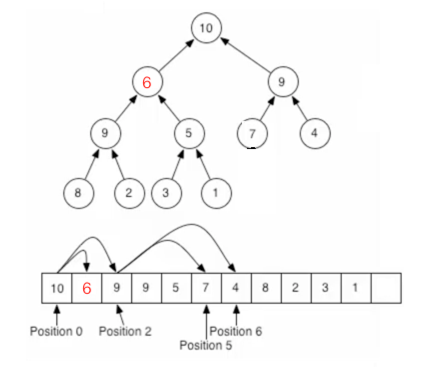
       堆（二叉堆）可以视为一棵完全的二叉树，完全二叉树的一个“优秀”的性质是，除了最底层之外，每一层都是满的，这使得堆可以利用数组来表示（普通的一般的二叉树通常用链表作为基本容器表示），每一个结点对应数组中的一个元素。

       对于7在数组存放的position=2，而它的子元素6的position=5=2*2[也就是父元素存放的位置]+1、子元素4的position=6=2*2[也就是父元素存放的位置]+2;同样对于11在在数组存放的position=0，而它的子元素10的position=1=2*0[也就是父元素存放的位置]+1、子元素7的position=2=2*0[也就是父元素存放的位置]+2;所以对于i个元素，它的左右子节点在下标以0开始的数组中的位置分别为：2*i+1、2*i+2。那脑补一下，对于不完全二叉树，如果用数组来存放会有什么问题呢？当然是中间有很多空的元素啦，所以说对于不完全二叉树最好是用链表来存储~。

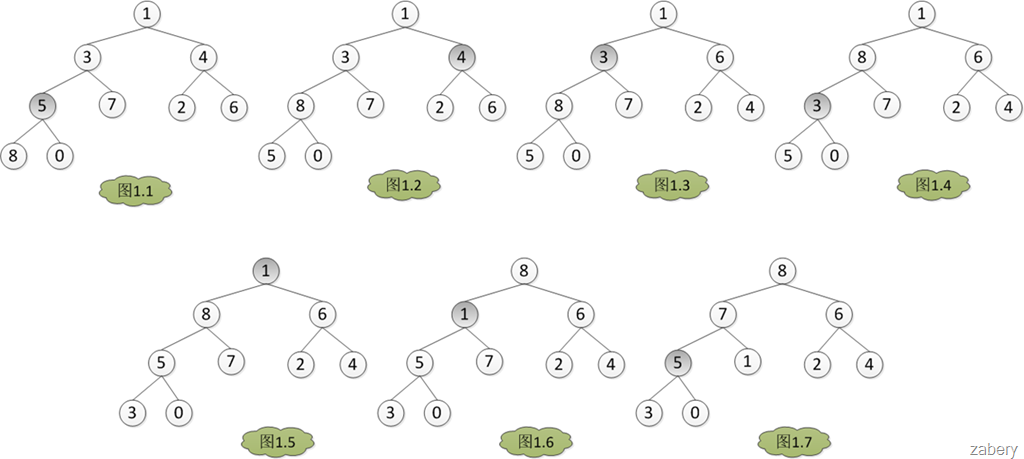
       堆的构建过程示例：建堆的核心内容是调整堆，使二叉树满足堆的定义（每个节点的值都不大于其父节点的值）。调堆的过程应该从最后一个非叶子节点开始，假设有数组A = {1, 3, 4, 5, 7, 2, 6, 8, 0}。那么调堆的过程如下图，数组下标从0开始，A[3] = 5开始。分别与左孩子和右孩子比较大小，如果A[3]最大，则不用调整，否则和孩子中的值最大的一个交换位置，在图1中是A[7] > A[3] > A[8]，所以A[3]与A[7]对换，从图1.1转到图1.2。

        二叉堆（英语：binary heap）是一种特殊的堆，二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。二叉堆一般用数组来表示。如果根节点在数组中的位置是1，第n个位置的子节点分别在2n和 2n+1。因此，第1个位置的子节点在2和3，第2个位置的子节点在4和5。以此类推。这种基于1的数组存储方式便于寻找父节点和子节点。如果存储数组的下标基于0，那么下标为i的节点的子节点是2i + 1与2i + 2；其父节点的下标是⌊floor((i − 1) ∕ 2)⌋。函数floor(x)的功能是“向下取整”，或者说“向下舍入”，即取不大于x的最大整数（与“四舍五入”不同，向下取整是直接取按照数轴上最接近要求值的左边值，即不大于要求值的最大的那个值）。比如floor(1.1)、floor(1.9)都返回1。对于堆定义中的堆结构插入元素：对于二叉堆来说，要插入一个新元素其整个过程是怎么样的呢？这里还是以我们之前的那个二叉堆进行说明，以插入"9"为例：

       目前肯定不满足二叉堆的要求，父接点6是小于新插入的节点9的，所以两者进行位置交换：

同样的思路，父节点7比子节点9要小，所以需要调换位置:

       至此元素插入完成，也符合二叉堆父元素大于子元素的规则，从添加过程中可以发现：只需更改待比较的元素，其它的任何元素位置不需要动，所以效率还是很高的。对于堆定义中的堆结构删除元素：这里以删除根结点为例【因为删除根节点是最重要的，所以以它为例】，整个过程如下：

       这时当然是不符合二叉堆的规则，接着这样来做：

        同理继续进行处理：

      继续：

       经过这些动作之后就将一个根结点给删除掉了，可以发现其实跟插入一个元素一样，只需更改待比较的元素，其它的任何元素位置不需要动，那像这种每次移除掉最大的值有啥用呢？堆排序就产生了，因为每次从根节点拿肯定是最大的数【以最大堆来说】，这样拿出来的数就成了一个有序的数列了。注意：对于一个很大的堆，这种存储是低效的。因为节点的子节点很可能在另外一个内存页中。B-heap是一种效率更高的存储方式，把每个子树放到同一内存页。如果用指针链表存储堆，那么需要能访问叶节点的方法。可以对二叉树“穿线”(threading)方式，来依序遍历这些节点。

四、堆排序动态示例图

五、堆排序Java代码实现

package com.luna.sort;public class HeapSortMaxAndMin{public static void main(String[] args) {int[] array = { 19, 38, 7, 36, 5, 5, 3, 2, 1, 0, 56 };System.out.println("排序前:");for (int i = 0; i < array.length; i++) {System.out.print(array[i] + ",");}System.out.println();System.out.println("分割线---------------");heapSort(array);System.out.println("排序后:");for (int i = 0; i < array.length; i++) {System.out.print(array[i] + ",");}}public static void heapSort(int[] array) {if (array == null || array.length == 1)return;buildArrayToHeap(array); //将数组元素转化为大顶堆/小顶堆for (int i = array.length - 1; i >= 1; i--) {// 经过上面的一些列操作，目前array[0]是当前数组里最大的元素，需要和末尾的元素交换，然后拿出最大的元素swap(array, 0, i);/*** 交换完后，下次遍历的时候，就应该跳过最后一个元素，也就是最大的那个* 值，然后开始重新构建最大堆堆的大小就减去1，然后从0的位置开始最大堆*/
//			buildMaxHeap(array, i, 0);buildMinHeap(array, i, 0);}}// 构建堆public static void buildArrayToHeap(int[] array) {if (array == null || array.length == 1)return;//递推公式就是 int root = 2*i, int left = 2*i+1, int right = 2*i+2;int cursor = array.length / 2;for (int i = cursor; i >= 0; i--) { // 这样for循环下，就可以第一次排序完成
//			buildMaxHeap(array, array.length, i);buildMinHeap(array, array.length, i);}}//大顶堆public static void buildMaxHeap(int[] array, int heapSieze, int index) {int left = index * 2 + 1; // 左子节点int right = index * 2 + 2; // 右子节点int maxValue = index; // 暂时定在Index的位置就是最大值// 如果左子节点的值，比当前最大的值大，就把最大值的位置换成左子节点的位置if (left < heapSieze && array[left] > array[maxValue]) {maxValue = left;}// 如果右子节点的值，比当前最大的值大，就把最大值的位置换成右子节点的位置if (right < heapSieze && array[right] > array[maxValue]) {maxValue = right;}// 如果不相等说明，这个子节点的值有比自己大的，位置发生了交换了位置if (maxValue != index) {swap(array, index, maxValue); // 就要交换位置元素// 交换完位置后还需要判断子节点是否打破了最大堆的性质。最大堆性质：两个子节点都比父节点小。buildMaxHeap(array, heapSieze, maxValue);}}//小顶堆public static void buildMinHeap(int[] array, int heapSieze, int index) {int left = index * 2 + 1; // 左子节点int right = index * 2 + 2; // 右子节点int maxValue = index; // 暂时定在Index的位置就是最小值// 如果左子节点的值，比当前最小的值小，就把最小值的位置换成左子节点的位置if (left < heapSieze && array[left] < array[maxValue]) {maxValue = left;}// 如果右子节点的值，比当前最小的值小，就把最小值的位置换成左子节点的位置if (right < heapSieze && array[right] < array[maxValue]) {maxValue = right;}// 如果不相等说明这个子节点的值有比自己小的，位置发生了交换了位置if (maxValue != index) {swap(array, index, maxValue); // 就要交换位置元素// 交换完位置后还需要判断子节点是否打破了最小堆的性质。最小性质：两个子节点都比父节点大。buildMinHeap(array, heapSieze, maxValue);}}// 数组元素交换public static void swap(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}
}

         大顶堆优化实现算法：

import java.util.Arrays;public class MaxHeapSort {private int[] arr;public MaxHeapSort(int[] arr){this.arr = arr;}/*** 堆排序的主要入口方法，共两步。*/public void sort(){/**  第一步：将数组堆化*  beginIndex = 第一个非叶子节点。*  从第一个非叶子节点开始即可。无需从最后一个叶子节点开始。*  叶子节点可以看作已符合堆要求的节点，根节点就是它自己且自己以下值为最大。*/int len = arr.length - 1;int beginIndex = (len - 1) >> 1; for(int i = beginIndex; i >= 0; i--){maxHeapify(i, len);}/** 第二步：对堆化数据排序* 每次都是移出最顶层的根节点A[0]，与最尾部节点位置调换，同时遍历长度 - 1。* 然后从新整理被换到根节点的末尾元素，使其符合堆的特性。* 直至未排序的堆长度为 0。*/for(int i = len; i > 0; i--){swap(0, i);maxHeapify(0, i - 1);}}private void swap(int i,int j){int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}/*** 调整索引为 index 处的数据，使其符合堆的特性。* @param index 需要堆化处理的数据的索引* @param len 未排序的堆（数组）的长度*/private void maxHeapify(int index,int len){int li = (index << 1) + 1; // 左子节点索引int ri = li + 1;           // 右子节点索引int cMax = li;             // 子节点值最大索引，默认左子节点。if(li > len) return;       // 左子节点索引超出计算范围，直接返回。if(ri <= len && arr[ri] > arr[li]) // 先判断左右子节点，哪个较大。cMax = ri;if(arr[cMax] > arr[index]){swap(cMax, index);      // 如果父节点被子节点调换，maxHeapify(cMax, len);  // 则需要继续判断换下后的父节点是否符合堆的特性。}}/*** 测试用例* 输出：* [0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9]*/public static void main(String[] args) {int[] arr = new int[]{3,5,3,0,8,6,1,5,8,6,2,4,9,4,7,0,1,8,9,7,3,1,2,5,9,7,4,0,2,6};        new MaxHeapSort(arr).sort();        System.out.println(Arrays.toString(arr));}}

原文地址：https://blog.csdn.net/u011635492/article/details/83046477