文章目录
- 堆排序
- 1. 排序思路
- 2. 如何建成大根堆
- 2.1. 将待排序的数据看成一个完全二叉树。
- 2.2. 建堆思想
- 2.3. 建堆步骤
- 2.3.1.先将最后一棵子树建成大根堆
- 2.3.2.将其余子树建成大根堆
- 2.3.3. 代码分析
- 3 如何实现堆排序
- 3.1 排序思路
- 3.2 代码实现的思路
- 3.3 代码分析
- 3.4 排序过程
- 4. 整体代码展示

堆排序

1. 排序思路
- 将一组数据建成大根堆。
- 定义一个end来记录此时堆末尾元素的位置。
- 每排序好一个,end值就减一个。
- 在排序的过程中要保障堆时刻为大根堆。
- 开始排序时,也要保证是大根堆。
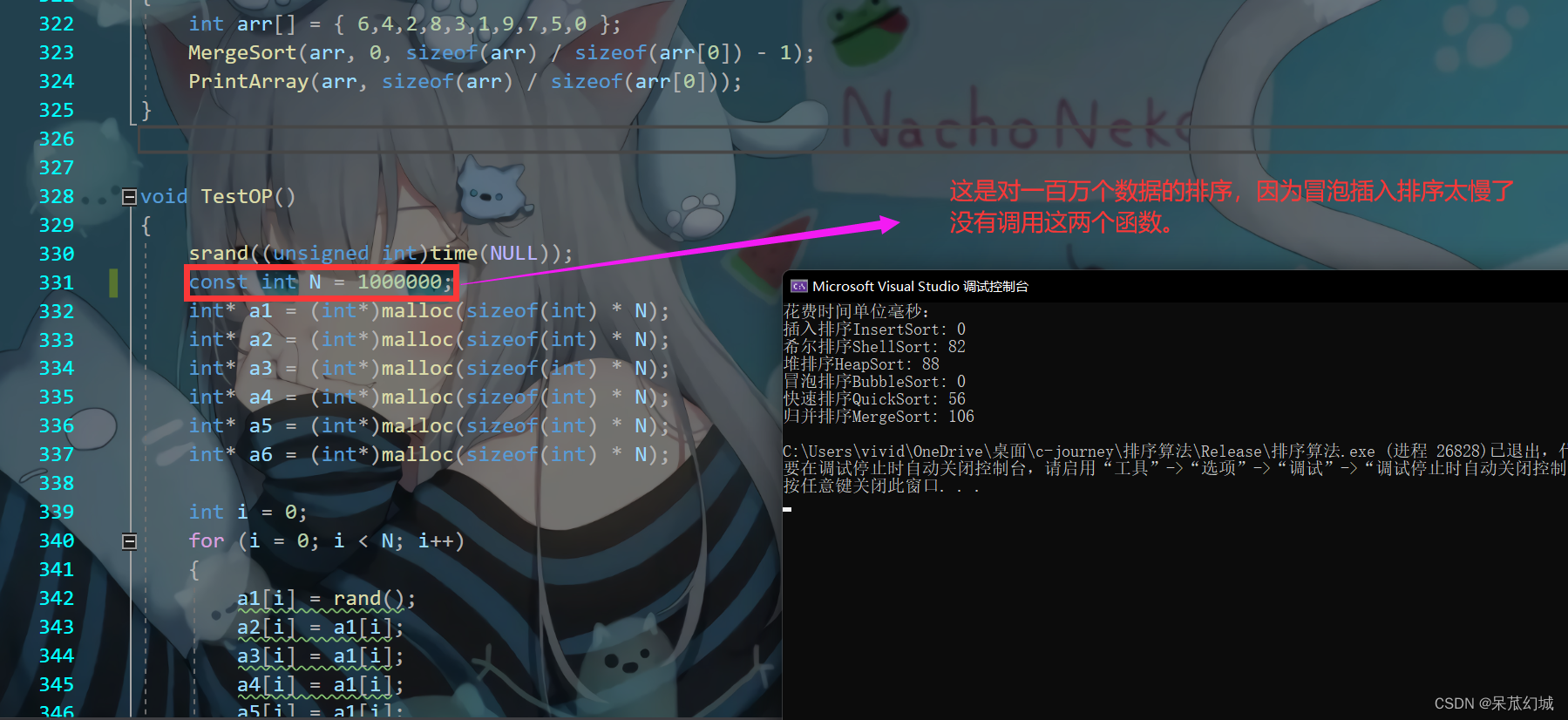
待排序的数据:27, 15, 19, 18, 28, 34, 65, 49, 25, 37
因为堆实际上是在二叉树的基础上做的一些调整。
在操作堆的时候本质是利用了二叉树的思想。
2. 如何建成大根堆
给每一个数据一个下标值。

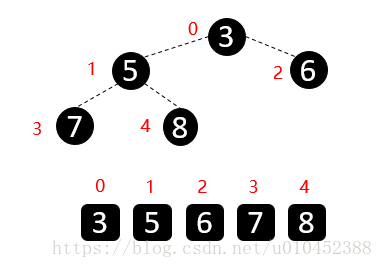
2.1. 将待排序的数据看成一个完全二叉树。
下图是排列好的二叉树。

但是它此时既不是大根堆也不是小根堆,即不是一个堆。
要将它变成一个堆,要先将它变成大根堆或者小根堆。
2.2. 建堆思想
如果是要建立成大根堆,先将它的子树全部建成大根堆。此时,这棵树整体也就变成了一个大根堆。

先将图中画红圈的建成大根堆,建成后,整棵树就是一个大根堆了。
有两个方法:
- 从无到有的建立堆,获取一个数据的同时将它建立为一个大根堆。一边获取数据,一边的建堆。
如果有两个数据,就将两个数据建成堆;若四个数据,就将四个数据建成堆。 - 先从最后一棵子树的根节点开始调整,将它建成大根堆;再将它前面的结点逐渐建成大根堆;最后整体就是一个大根堆了。(向下调整)
2.3. 建堆步骤
实现向下调整
2.3.1.先将最后一棵子树建成大根堆
- 最后一棵子树的孩子结点的下标是数组的长度减1。(10 - 1)
- 已知孩子结点,求父亲结点的公式:(i - 1) / 2,i 是孩子结点的下标。
- 现在得到了最后一棵子树的孩子和父亲结点的下标。(孩子:9,父亲:4)
- 比较两个结点的值,将较大的结点交换到对应父节点的位置。
- 若父节点为最大值,则不需要交换。
最后一棵子树建堆后:

图中的4下标和9下标的结点进行了交换。
2.3.2.将其余子树建成大根堆
第1步:
- r 记录父亲结点的下标;i 记录左右最大值的下标。
- r - - ,找到新的子树的根节点。
- 找到了根节点,可以访问到子节点。

第2步:
- i 结点始终记录左右子节点的最大值。
- 将这个最大值节点与当前 r 节点交换。

交换后:
下图的3下标和7下标交换了。

第3步:
- r - -,r 指向了2下标所在根节点的位置。
- i 指向左右子节点的最大值。

第4步:
- 交换 r 和 i 指向的两个结点。

第5步:
- r - -,r 指向了1下标所在根节点的位置。
- i 指向左右子节点的最大值。

第6步:
- 交换 r 和 i 指向的两个结点。

走到这里就会发现,3下标位置的根节点又不是大根堆了。
要让 r 重新指向3下标,i 再指向左右孩子最大值。
第7步:
- r 指向 i ,i 指向(2 * p + 1)的位置(下标7处),p 代表的是父节点下标。
- i 再指向左右孩子最大值。

第8步:
- 比较 r 和 i 之后,交换较大到根节点位置。

程序并不知道这一步交换完成后,15有没有左右节点了。
因此并不能确定交换一次 r 和 i 结点之后就为大根堆了。
解决办法:
- r 指向 i 的位置,i 指向 (2 * p + 1) 的位置(下标17处),p 代表的是父节点下标。
- i 再指向左右孩子最大值。

此时 i 的值大于数据个数(10)的最大下标值(9),此时说明15左右没有孩子。
此时如果 i 的值乘2加1大于9,就说明此时的 i 指向的就是最后一个结点了。
2.3.3. 代码分析
for (int parent = (array.length - 1 - 1) / 2; parent >= 0 ; parent--) {}
- parent 代表的是父节点 r 。
- 先求出数组长度,减1表示得到末尾元素下标,再减1表示得到每一个父节点。
- 当 parent 小于0时,调整完毕。
shiftDown(array, parent, array.length);
- 循环调用向下调整方法。
public static void shiftDown(int[] array, int parent, int len) {}
- 参数 len 是每棵子树调整的结束位置。
- 结束位置不能大于 len 。
int child = (2 * parent) + 1;
- 求得孩子结点,代表的是 i 。
while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {child++;}}

- child < len 保证有左孩子,len 是数组长度。
- child + 1 < len 保证不越界。
- array[child] < array[child + 1] 保证 child 是左右最大值。
if (array[child] > array[parent]) {
}
- 比较孩子结点和父节点的值。
if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = 2 * parent + 1;}
- 如果孩子结点大于父节点就交换这两个结点。
- 父节点指向子节点。
- 孩子结点指向新的位置。
public static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}
- 交换方法的实现。
最终实现的大根堆:

3 如何实现堆排序
3.1 排序思路
- 将堆顶元素与堆的最后一个元素交换,此时堆的末尾位置就是最大的元素了。
- 每一次交换后要保证堆是大根堆。
- 若堆不是大根堆,就调用向下调整重新建成大根堆。
- 重新交换堆顶元素与堆的末位置元素。
3.2 代码实现的思路
- 定义一个 end 来记录此时堆的末尾位置元素的位置。(元素个数 - 1)
- 每排序好一个数据,end 就减去1。
- 若此时的堆不是大根堆,调用向下调整重新实现为大根堆。
- 若刚开始排序时,堆不为大根堆,则要将它建成大根堆。
3.3 代码分析
creatBigHeap(array);
- 先调用建堆方法建堆。
int end = array.length - 1;
- 数组长度减1求的是堆末尾位置元素的下标。
while (end > 0) {swap(array, 0, end);shiftDown(array, 0, end);end--;}
- 循环调用交换方法交换0下标和end位置的值。
- 0 下标即使堆顶元素的位置。
- 循环调用向下调整方法建成大根堆。
- 每次交换后,end每次减少一个。
3.4 排序过程
-
交换一次后

-
此时不为大根堆了,先建成大根堆,再交换。

-
65 是排序好的了,所以在重新建成大根堆的时候不需要处理65,交换第2次。

-
按照上面的步骤会逐渐排成:

4. 整体代码展示
public static void heapSort(int[] array) {creatBigHeap(array);int end = array.length - 1;while (end > 0) {swap(array, 0, end);shiftDown(array, 0, end);end--;}}//建堆
public static void creatBigHeap(int[] array) {for (int parent = (array.length - 1 - 1) / 2; parent >= 0 ; parent--) {//调用向下调整shiftDown(array, parent, array.length);}
}//向下调整的方法
public static void shiftDown(int[] array, int parent, int len) {int child = (2 * parent) + 1;while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {child++;}if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = 2 * parent + 1;}else {break;}}
}//交换的方法
public static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}