C语言表达式专练

article/2025/9/23 17:42:41

1、以下表达式值为3的是
A)16-13%10
B)2+3/2
C)14/3-2
D)(2+6)/(12-9)
2、设有说明语句:int k=7，x=12;则以下能使值为3的表达式是
A) x%=(k%=5)
B)x%=(k-k%5)
C)x%=k-k%5
D)(x%=k)-(k%=5)
3、若x、i、j和k都是int型变量，则执行表达式x=(i=4,j=16,k=32)后x的值为
A）4
B)16
C)32
D) 52
4、设所有变量为整型，则表达式（a=2,b=5,b++,a+b)的值是
A)7
B)8
C) 6
D)2
5、已知各变量的类型说明如下:
int k,a, b;
unsigned long w=5;
double
x=1.42;
则以下不正确的表达式是
A) x%(-3)
B)w+=一2
C)k=(a=2,b=3,a+b)
D)a+=a-=(b=4)*(a=3)
6、已知各变量的类型说明如下:
int i=8,k，a，b;
unsigned long w=5;
double x=1.42,y=5.2;
则以下正确的表达式是
A) a+=a-=(b=4)*(a=3)
B) a=a*3=2
C)x%(-3)
D) y= float(i)
7、以下不正确的叙述是
A)在C程序中,逗号运算符的优先级最低
B)在C程序中，APH和aph是两个不同的变业
C)若a和b类型相同,在执行了赋值表达式a=k后by中的值将放人a中,而b
中的值不变
D)当从键盘输入数据时，对于整型变量只能输入整型数值,对于实型变量只能输入实型数值
8、以下正确的叙述是
A)在C程序中，每行中只能写一条语句
B)若a是实型变量,C程序中允许赋值a=10,因此实型变量中允许存放整
型数
C)在C程序中,无论是整数还是实数,都能被准确无误地表示
D)在C程序中,%是只能用于整数运算的运算符
9、已知字母A的ASCII码为十进制数65,且定义c2为字符型变量,则执行语句
~c2='A'+'6'-'3';后,c2中的值为
A)D
B) 68
C)不确定的值
D)C
10、在C语言中，要求运算数必须是整型的运算符是
A)/
B)十十
C)!=
D)%
11、若有说明语句:char c='\72';则变量c
A)包含1个字符
B)包含2个字符
C)包含3个字符
D)说明不合法，c的值不确定
12、若有定义语句:int a=7;float x=25,y=4.7;则表达式x+a%3*(int)(x+y)%2/4的值是
A) 2.500000
B) 2.750000
C) 3.500000
D) 0.000000
13、sizeof(float)是
A)一个双精度型表达式
B)一个整型表达式
C)一种函数调用
D)一个不合法的表达式
14、设变量a是整型，f是实型，i是双精度型，则表达式10+'a'+i*f值的数据
类型为
A) int
B) float
C) double
D)不确定
15、设以下变量均为int类型,则值不等于7的表达式是
A)(x=y=6,x+y,x+1)
B)(x=y=6,x+y,y+1)
C)(x=6,x+1,y=6,x+y)
D)(y=6,y+l,x=y,x+1)
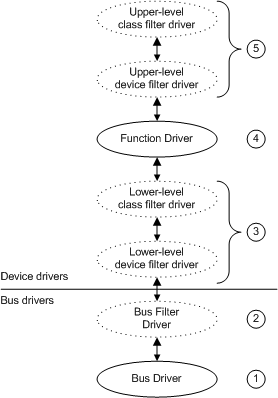
16、若有代数式如图所示,则正确的C语言表达式是