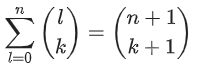0. 前言

组合数求解有很多种方式，不同的方式对应这不同的时间复杂度，难以程度也是不尽相同。根据数据范围选择对应的方法即可。

1. 预处理组合数+组合递推式

885. 求组合数 I

重点： 组合公式、组合递推式

组合公式：
$$C_a^b=\left(\genfrac{}{}{0ex}{}{a}{b}\right)=\frac{a\times (a-1)\times \cdots \times (a-b+1)}{1\times 2\times 3\times \cdots \times b}=\frac{a!}{b!(a-b)!}$$

时间复杂度分析：

• 10w 组询问
• 一个组合数最坏需要 2000 次运算
• 则暴力总共的时间复杂度为 2000 * 10w，为 2 亿次运算，这妥妥的超时。
• 但是能发现，a、b 都比较小，总共可能出现的 (a,b) 对就是 2000 * 2000 = 400w 对不同的 $C_a^b$
• 所以可以预处理出来所有的情况，有组合递推式为 $$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$$从实际出发，$C_a^b$ 表示从 $a$ 个苹果当中选 $b$ 个苹果的方案数，那么可以将所有选法分为两种情况，即从 $n$ 个苹果中挑出来一个苹果，这个苹果被选中，这个苹果不被选中，就这两种情况。 则包含这个特殊苹果的方案数就是 $C_{a-1}^{b-1}$，不包含这个特殊苹果的方案数是 $C_{a-1}^b$

#include <iostream>using namespace std;typedef long long LL;const int N = 2010, MOD = 1e9+7;int n;
int c[N][N];void init() {for (int i = 0; i < N; ++i) for (int j = 0; j <= i; ++j)if (!j) c[i][j] = 1;else c[i][j] = (c[i-1][j] + c[i-1][j-1]) % MOD;
}int main() {init();int n;cin >> n;while (n --) {int a, b;cin >> a >> b;cout << c[a][b] << endl;}return 0;
}

2. 预处理阶乘+逆元

886. 求组合数 II

重点： 组合公式、组合递推式

组合公式：
$$C_a^b=\frac{a!}{b!(a-b)!}$$

预处理所有的模 $p$ 意义下的阶乘，我们假设用 $fact[i]=i!\%(10^9+7)$。这个事情是简单的，所以分子分母都可以简单的得到。但是众所周知：$$\frac{a}{b}\%p\ne \frac{a\%p}{b\%p}$$
但是，我们可以采用逆元，将除法变成乘法。

所以我们可以再预处理出 $infact[i]=(i!{)}^{-1}\%(10^9+7)$

此时，有：$$C_a^b=fact[a]\times infact[b-a]\times infact[b]$$

求逆元，由于 p=1e9+7，那么可以采用快速幂和费马小定理，时间复杂度就是 $O(nlogn)$。

注意：

• 能开 long long 的地方建议全开
• 数组中间计算值也是相当容易溢出的，记得及时对中间结果取模

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;const int N = 1e5+5, MOD = 1e9+7;int fact[N], infact[N];int qmi(int a, int k, int p) {LL res = 1;while (k) {if (k & 1) res = (LL)res * a % p;k >>= 1;a = (LL)a * a % p;}return res;
}int main() {fact[0] = infact[0] = 1;for (int i = 1 ; i < N; ++i) {fact[i] = (LL)fact[i - 1] * i % MOD;infact[i] = (LL)infact[i - 1] * qmi(i, MOD - 2, MOD) % MOD;}int n;cin >> n;while (n --) {int a, b;cin >> a >> b;cout << (LL)fact[a] * infact[a - b] % MOD * infact[b] % MOD << endl;}return 0;
}

3. 卢卡斯定理

887. 求组合数 III

重点： 卢卡斯定理

在此推荐一个大佬博客，很清楚，简介

再推荐一个，我的证明就是仿照这位大佬的

模板代码：

#include <iostream>using namespace std;typedef long long LL;int qmi(int a, int k, int p) {int res = 1 % p;while (k) {if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}// 定义求解
int C(int a, int b, int p) {if (b > a) return 0;int res = 1;for (int i = 1, j = a; i <= b; ++i, --j) {res = (LL)res * j % p;res = (LL)res * qmi(i, p - 2, p) % p;}return res;
}int lucas(LL a, LL b, LL p) {               // 注意LL参数类型if (a < p && b < p) return C(a, b, p);return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;     // 递归让其到p范围内求解
}int main() {int n;cin >> n;while (n --) {LL a, b, p;cin >> a >> b >> p;cout << (LL)lucas(a, b, p) << endl;}return 0;
}

4. 高精度组合数

888. 求组合数 IV

重点： 高精度组合数、高精乘、分解质因数

直接从组合公式出发求解：
$$C_a^b=\left(\genfrac{}{}{0ex}{}{a}{b}\right)=\frac{a\times (a-1)\times \cdots \times (a-b+1)}{1\times 2\times 3\times \cdots \times b}=\frac{a!}{b!(a-b)!}$$

但是，这样显然需要实现高精乘、高精除这两个。

故，我们可以对其先分解质因数，然后组合结果保证为整数，即只需要实现高精乘即可。在此分解质因数也是采用组合公式的第二个，直接对阶乘进行质因数分解。

思路：

• 预处理 5000 内所有素数

• a! 的唯一分解式中求解素数 p 的倍数有一个快速的方法：a! = a/p + a/(p^2) + a/(p^3) +... 这里的所有除均为下取整，直至 p^k 大于 a。这样做的意义在于 a/p 可以得到 1 到 n 中有多少个数是 p 的倍数，a/(p^2) 理解为得到 1 到 n 中有多少个数是 p^2 的倍数…依次类推

• 这个乍一看肯定计算重复项了啊，但是实际上并没有。可以手动模拟一下 a = 8,p =2 的情况，注意这里是求解 8! 中质因子 2 出现的次数，此时结果应该是 7，因为 2，4，6，8 分别贡献 p 作为 2 时的 4 个数。 4，8 贡献了 p 作为 2^2 时的 2 个数，8 贡献了 p 作为 2^3 时的 1 个数。总共就是 7 个数

• 根据这个性质，求解阶乘中某个质因子出现的次数，一般来讲有两种写法，朴素版本和优化版本，代码均已给出

模板代码：

#include <iostream>
#include <algorithm>
#include <vector>using namespace std;const int N = 5005;int primes[N], cnt;
int sum[N];
bool st[N];void get_primes(int n) {for (int i = 2; i <= n; ++i) {if (!st[i]) primes[cnt ++] = i;for (int j = 0; primes[j] <= n / i; ++j) {st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}// 直观，有溢出风险
int get(int n, int p) {int res = 0,t = p;while (n >= p) {res += n / p;p *= t;}return res;
}// 精炼简介，完美版本
int get1(int n, int p) {int res = 0;while (n) {res += n / p;n /= p;}return res;
}vector<int> mul(vector<int> a, int b) {vector<int> C;int t = 0;for (int i = 0; i < a.size(); ++i) {t += a[i] * b;C.push_back(t % 10);t /= 10;}while (t) {C.push_back(t % 10);t /= 10;}return C;
}int main() {int a, b;cin >> a >> b;get_primes(a);for (int i = 0; i < cnt; ++i) {int p = primes[i];sum[i] = get(a, p) - get(b, p) - get(a - b, p);}vector<int> res;res.push_back(1);for (int i = 0; i < cnt; ++i) for (int j = 0; j < sum[i]; ++j)res = mul(res, primes[i]);for (int i = res.size() - 1; i >= 0; --i) cout << res[i];cout << endl;return 0;
}