定义:
从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。
公式:
在线性写法中被写作C(m,n)。
c(m,n)=p(m,n)/n!=m!/((m-n)!*n!)
性质:
1.互补性质
组合数性质如右图所示:
即从m个不同元素中取出n个元素的组合数=从m个不同元素中取出(m-n)个元素的组合数
这个性质很容易理解,例如C(9,2)=C(9,7),即从9个元素里选择2个元素的方法与从9个元素里选择7个元素的方法是相等的。
规定:C(m,0)=1
2.组合恒等式
若表示在n个物品中选取m个物品,则如存在下述公式: C(n,m)= C(n,n-m)= C(n-1,m-1)+C(n-1,m)
求法:
1、一般方法
直接套公式:
求出m!、n!、(m-n)!然后带人公式;
代码如下:
# include<stdio.h>
# include<math.h>
int f(int n){int i,m=1;for(i=1;i<=n;i++){m=m*i;}return m;
}
int main(){int n,m;scanf("%d %d",&n,&m);printf("%d\n",f(n)/(f(m)*f(n-m)));return 0;
}
稍微用点小技巧
long long C(int n,int m)
{if(m<n-m) m=n-m;long long ans=1;for(int i=m+1;i<=n;++i) ans*=i;for(int i=1;i<=n-m;++i) ans/=i;return ans;
}
2、杨辉三角
就算是long long最多20!左右;再大就会爆了
那就用到我们大数学家杨辉的三角了
: C(n,m)= C(n,n-m)= C(n-1,m-1)+C(n-1,m)
#include<iostream>
using namespace std;
long long c[100][100];
inline void get_it(int n)
{c[0][0]=1;for (int i=1;i<=n;i++)for (int j=0;j<=i;j++)if (i==j ||j==0) c[i][j]=1;else c[i][j]=c[i-1][j]+c[i-1][j-1];
}
int main()
{get_it(60);for (int i=1;i<=60;i++){for (int j=1;j<=i;j++)cout<<c[i][j]<<" ";cout<<endl;}
}
理论上只要数组开的出来都可以,最多,emmm,反正比一般方法强。
3、快速组合数
这个要用快速幂:https://blog.csdn.net/weixin_43272781/article/details/85058595
主要是用在一般方法;求阶乘的时候。
我就不写了。
4、求余组合数
以上方法最多也就到long long的极限,当然超过long long的我们也存储不下了,但是如果我们只需要一部分高阶组合数,用杨辉三角太浪费了吧。而且一般题目会有求余的要求,那么接下来就是大招了。
证明:https://blog.csdn.net/arrowlll/article/details/52629448
1).扩展欧几里德:b*x+p*y=1 有解,x就是所求2).费马小定理:b^(p-1)=1(mod p),故b*b^(p-2)=1(mod p),所以x=b^(p-2)
1. n!/(m!*(n-m)! =x%p ,先对算出n!、m!、(n-m)!对p取模的余数,就转换为a/b=x%p;因为p为素数,所以等价于bx+py=a;然后用扩展的欧几里得定理算出 bx’+py’=1的解,x=x’*a,就得到了最终的x的值,即C(m,n)%p得值。
2.逆元 其实如果mod是素数 则b的逆元其实就是b^(mod-2)
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 ;
int inv(int a) { //return fpow(a, MOD-2, MOD); return a == 1 ? 1 : (long long)(MOD - MOD / a) * inv(MOD % a) % MOD;
}
LL C(LL n,LL m)
{ if(m < 0)return 0; if(n < m)return 0; if(m > n-m) m = n-m; LL up = 1, down = 1; for(LL i = 0 ; i < m ; i ++){ up = up * (n-i) % MOD; down = down * (i+1) % MOD; } return up * inv(down) % MOD;
}
3.当n和m比较大,mod是素数且比较小的时候(10^5左右),通过Lucas定理计算
Lucas定理:A、B是非负整数,p是质数。A B写成p进制:A=a[n]a[n-1]…a[0],B=b[n]b[n-1]…b[0]。
则组合数C(A,B)与C(a[n],b[n])C(a[n-1],b[n-1])…*C(a[0],b[0]) mod p同余
即:Lucas(n,m,p)=C(n%p,m%p)*Lucas(n/p,m/p,p)
#include<iostream>
//#include<algorithm>
using namespace std;
typedef long long ll;
int quick_power_mod(int a,int b,int m){//pow(a,b)%mint result = 1;int base = a;while(b>0){if(b & 1==1){result = (result*base) % m;}base = (base*base) %m;b>>=1;}return result;
}
//计算组合数取模
ll comp(ll a, ll b, int p) {//composite num C(a,b)%pif(a < b) return 0;if(a == b) return 1;if(b > a - b) b = a - b;int ans = 1, ca = 1, cb = 1;for(ll i = 0; i < b; ++i) {ca = (ca * (a - i))%p;cb = (cb * (b - i))%p;}ans = (ca*quick_power_mod(cb, p - 2, p)) % p;return ans;
}
ll lucas(ll n, ll m, ll p) {ll ans = 1;while(n&&m&&ans) {ans = (ans*comp(n%p, m%p, p)) % p;//also can be recusiven /= p;m /= p;}return ans;
}
int main(){ll m,n;while(cin>>n>>m){cout<<lucas(n,m,10007)<<endl;}return 0;
}
C(n % mod, m % mod) % mod; 如果太大还是利用上面的逆元来处理。
半预处理
由于Lucas定理保证了阶乘的数均小于p,所以可以讲所有的阶乘先预处理,优化C(n,m)
mod的要求:p<10^6,且为素数
有效范围:1<=n,m<=10^9
//半预处理
const ll MAXN = 100000;
ll fac[MAXN+100];
void init(int mod)
{ fac[0] = 1; for (int i=1; i<mod; i++){ fac[i] = fac[i-1] * i % mod; }
} //半预处理逆元求C(n,m)%mod
ll C(ll n, ll m)
{ if ( m>n ) return 0; return fac[n] * (GetInverse(fac[m]*fac[n-m], mod)) % mod;
} 
typedef long long LL;
const LL maxn(1000005), mod(1e9 + 7);
LL Jc[maxn];void calJc() //求maxn以内的数的阶乘
{Jc[0] = Jc[1] = 1;for(LL i = 2; i < maxn; i++)Jc[i] = Jc[i - 1] * i % mod;
}
/*
//拓展欧几里得算法求逆元
void exgcd(LL a, LL b, LL &x, LL &y) //拓展欧几里得算法
{if(!b) x = 1, y = 0;else{exgcd(b, a % b, y, x);y -= x * (a / b);}
}LL niYuan(LL a, LL b) //求a对b取模的逆元
{LL x, y;exgcd(a, b, x, y);return (x + b) % b;
}
*///费马小定理求逆元
LL pow(LL a, LL n, LL p) //快速幂 a^n % p
{LL ans = 1;while(n){if(n & 1) ans = ans * a % p;a = a * a % p;n >>= 1;}return ans;
}LL niYuan(LL a, LL b) //费马小定理求逆元
{return pow(a, b - 2, b);
}LL C(LL a, LL b) //计算C(a, b)
{return Jc[a] * niYuan(Jc[b], mod) % mod* niYuan(Jc[a - b], mod) % mod;
}
例题
https://blog.csdn.net/weixin_43272781/article/details/85269419
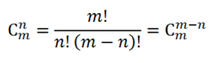










![[architecture]-DBG、DMB、DSB 和 ISB指令介绍](http://assets.processon.com/chart_image/604719347d9c082c92e419de.png)