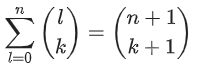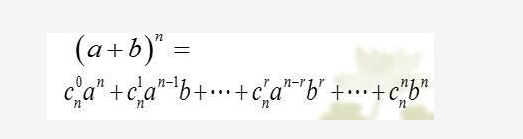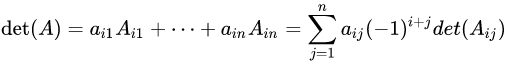摘自https://www.jianshu.com/p/718a5ac26238
逆元+快速幂解法
（一）基本概念
上面两种方法都使用了递归方法，递归方法有个缺陷，就是在数据较大时效率较低。所以这里要介绍一个种新的求组合算法。在了解此算法之前，要先了解一些概念。
1 同余
同余是数论中的重要概念。
给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)
例1：4 ≡ 9 (mod 5)，即4和9对模5同余
例2：13 ≡ 23（mod 10)，即13和23对模10同余

2 模的加减乘除运算
取模运算的等价变形适合加法、减法、乘法
(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p) % p
(a * b) % p = (a % p * b % p) % p
例3：(30 + 40) % 11 = 70 % 11 = 4
(30% 11 + 40%11) % 11 = (8 + 7) % 11 = 15 % 11 = 4
例4：(80 - 20) % 7 = 60 % 7 = 4
(80 % 7 - 20 % 7) % 7 = (3 - 6) % 7 = -3 % 7 = 4 （取模是让商尽可能小，所以这里有 -3 / 7 = -1 …… 4)
例5：(18 * 20) % 7 = 360 % 7 = 3
（18%7 * 20%7）% 7 = （4 * 6）% 7 = 3
但是，取模运算的等价变形不符合除法
a/b % p ≠ (a%p / b%p) % p
例6：（100 % 20）% 11 = 5 % 11 = 5
（100%11 / 20%11) % 11 = (1 / 9) % 11 = 0 % 11 = 0
3 逆元
逆元：对于a和p，若gcd(a, p) = 1（a和p互素）且 ab%p≡1，则称b为a%p的逆元。
那这个逆元有什么用呢？试想一下求(a / b)%p，如果你知道b%p的逆元是c，那么就可以转变成(a/b)%p = (a/b) * 1 % p = (a / b) * (b c % p) % p = a*c % p = (a%p) (c%p) % p，这样的话，除法运算就可以转化为乘法运算。
那怎么求逆元呢？这时候就要引入强大的费马小定理！

费马小定理：对于a和素数p，满足a^(p-1) % p ≡ 1

接着因为a^(p−1) = a^(p−2) * a，所以有a^(p−2) * a % p ≡ 1。
对比逆元的定义可得，a^(p−2)就是a的逆元。
所以问题就转换成求解a^(p−2)，即变成求快速幂的问题了。
4 快速幂
这部分的内容可以参考 小朋友学算法（6）：求幂pow函数的四种实现方式 中的第四种方法
（二）逆元 + 快速幂求组合思路
现在目标是求C(n, m) %p，p为素数（经典p=1e9+7）。
虽然有C(n, m) = n! / [m! (n - m)!]，但由于取模的性质对于除法不适用，则有

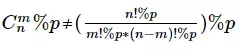
所以需要利用逆元把“除法”转换成“乘法”，才能借助取模的性质计算组合数。
求解C(n, m)%p的步骤：
（1）通过循环，预先算好所有小于max_number的阶乘（%p）的结果，存到fac[max_number]里 (fac[i] = i! % p)
（2）求m! % p的逆元（即求fac[m]的逆元）：根据费马小定理，x%p的逆元为x^(p−2)， 因此通过快速幂，求解fac[m]^(p−2) % p，记为M
（3）求(n-m)! % p的逆元：同理就是求解fac[n−m]^(p−2) % p，记为NM
（4）C(n, m) % p = ((fac[n] * M) % p * NM) % p

具体代码如下：

#include <cstdio>
using namespace std;#define MAX_NUMBER 100000
//快速幂求x^n%mod
long long quick_pow(long long x, long long n, long long mod)
{long long res = 1;while (n){if (n & 1){res = res * x % mod;}x = x * x % mod;n >>= 1;}return res;
}long long fac[MAX_NUMBER+5];
long long n, m, p;int main()
{while (~scanf("%lld %lld %lld", &n, &m, &p)){//预处理求fac，fac[i] = i!%pfac[0] = 1;for (int i = 1; i <= n; i++){fac[i] = fac[i - 1] * i % p;}//组合数 = n!*(m!%p的逆元)*((n-m)!%p的逆元)%pprintf("%lld\n", fac[n] * quick_pow(fac[m], p - 2, p) % p * quick_pow(fac[n - m], p - 2, p) % p);}
}