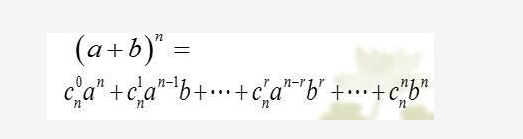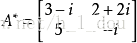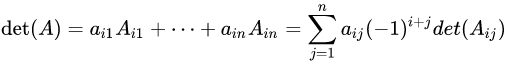题目描述:
在ACM竞赛现在叫JB竞赛?中,经常会遇到组合数取模的题目;就我现在的水平而言,大概分为以下三类,以后遇到新的方法会在做补充;
第一种:

n和m都较小 (<1000),在这个数据范围内,我们可以直接用杨辉三角O(n^2)的复杂度内预处理出所有的组合数,然后直接输出即可;典型例题就是给你一个二项式,例如:

这样子的题目,组合数我们可以O(n2)预处理出来(利用递推式子来处理)。ab之类的东西我们可以用快速幂logn的复杂度内处理出来; 这种题由于数据范围过小,当水题处理就行;
代码大概是这样:
#include <bits/stdc++.h>
using namespace std;#define MOD 10007
#define long long longlong pow_MOD(long a, long b)
{long tmp = 1;while(b){if(b & 1){tmp = (tmp % MOD * a % MOD) % MOD;}a = (a * a) % MOD;b >>= 1;}return tmp;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int p, q, a, b, k;cin >> p >> q >> k >> a >> b;long tmp = 1;for(int i = 1; i <= b; i++){if(tmp % i == 0){tmp = tmp / i * (k - i + 1) % MOD;}else{tmp = tmp * (k - i + 1) / i % MOD;}}//cout << "tmp = " << tmp << endl;cout << ((tmp % MOD) * (pow_MOD(p, a) % MOD) * (pow_MOD(q, b) % MOD)) % MOD;return 0;
}
第二种
给定的n和m不太大 (1e5范围左右),给定的p较大(一般是1e9+7);这时候如果我们还是利用杨辉三角之类的东西就不行了;第一空间不足,没办法开出来1e5*1e5这么大的数组,第二在时间也是不允许的n^2的复杂度,肯定会T掉;所以我们需要利用线性方法递推组合数 公式大概是这样

就是可以依赖前一项的组合数推出下一项的组合数,在O(n)的时间内可以出结果;但是,这里由于在求余过程中,除法是不具有同余性;即
(a + b) % mod = (a % mod + b % mod) % mod
(a - b) % mod = (a % mod - b % mod) % mod
(a * b) % mod = (a % mod * b % mod) % mod
加法、减法、乘法都是有这个性质,只有除法不满足,所以中间直接模的话会出错;所以我们得预处理一下1-n关于p的逆元,把除法换为乘法。这样就没啥问题了;
显然,他一共要走n+m-2步,所以答案就是;但是受限于数据范围,我们得先预处理一下逆元,然后线性推组合数即可;
对了,处理逆元有很多种办法;
如果要求单个数字的逆元我们可以用扩展欧几里得或者快速幂(建议exgcd,更快点);
如果要处理的是一堆,就是1-n所有数字的逆元,我们可以用欧拉筛打出逆元表,或者直接利用递推inv[i] = (p - p / i) * (inv[p % i]) % p;这样子;
经典问题就是走迷宫之类的东西,例如:

我们先用线性推预处理逆元,然后用组合数的递推式递推组合数,即可AC
#include <bits/stdc++.h>
using namespace std;#define long long long
#define MOD 1000000007
#define N 1000010long inv[N];int main()
{long n, m;cin >> n >> m;inv[1] = 1;if(n > m)swap(n, m);for(int i = 2; i <= n; i++){inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;}long tmp = 1, val = n + m - 2;for(int i = 1; i <= n-1; i++){tmp = tmp % MOD * (val - i + 1) % MOD * inv[i] % MOD;}cout << tmp << endl;return 0;
}第三种
第三种就是n和m都较大(1e9左右), p较小(1e5左右);这种情况下,第二种做法都不行了,这时候我们得用Lucas定理来解决;Lucas就是把大化小把一个大的组合数拆分为很多小的组合数乘积的结果;有兴趣可以了解一下;就是将n,m都改为p进制,然后累乘;这样子;
HDU-3037
#include <bits/stdc++.h>
using namespace std;#define long long long
#define N 100010long a[N], p;long exgcd(long a, long b, long &x, long &y)
{if(b == 0){x = 1;y = 0;return a;}long r = exgcd(b, a%b, x, y);long tmp = x;x = y;y = tmp - a / b * y;return r;
}long C(long n, long m)
{if(n < m)return 0;long x, x1, y, y1;exgcd(a[m], p, x, y);exgcd(a[n-m], p, x1, y1);x = (x + p) % p;x1 = (x1 + p) % p;return ((a[n] % p) * x % p * x1 % p) % p;
}long Lucas(long n, long m)
{if(!m)return 1;return C(n % p, m % p) * Lucas(n / p, m / p) % p;
}int main()
{int t;cin >> t;while(t--){long n, m;cin >> n >> m >> p;a[0] = 1;for(int i = 1; i <= p; i++){a[i] = (a[i-1] * i) % p;}cout << Lucas(n+m, m) << endl;}return 0;
}