逆元简介
同余符号 ≡
先bb一下 ≡,这个符号有三个意思,再这里用到的意思为“同余符号”。≡ 的介绍
两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余
记作a≡b(mod m)
读作a同余于b模m,或读作a与b关于模m同余。
比如26≡14(mod 12)。
什么是逆元
如果一个线性同余方程 ax ≡ 1(mod b) ,则 x 称为 a mod b 的逆元.
逆元的含义
模b意义下,1个数a如果有逆元x,那么除以a相当于乘以x。
也就是(a/b)%p=(ax)%p=(a%p)(b%p)%p
那么问题来了,这逆元有啥用吗,这个问题问的好啊
如果我们要求一个组合数C(n,m)%p=(n!/(n-m)!*m!)%p,但是取模的性质对于除法不适用啊。
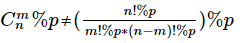
但当这个n和m很大时又不得不取模,不取模就会溢出。所以就可以用逆元来把乘法代替除法。
怎么求逆元
暴力O( P)求逆元
先举这个最简单最暴力的方法,这样便于理解逆元。具体思路就是枚举1~p-1,检查是否有符合条件的a*x=1(mod p)。时间复杂度为O(P)。
#include <iostream>
#include <cstdio>
using namespace std;
int main()
{int a,p;cin>>a>>p;for(int x=1;x<p;x++){if(x*a%p==1) {printf("%d\n",x);break;}}return 0;
}
扩展欧几里得法
给定模数p,求a的逆元相当于求解ax=1(mod p)
这个方程可以转化为ax-py=1
然后套用求二元一次方程的方法,用扩展欧几里得算法求得一组x0,y0和gcd (最大公约)
检查gcd是否为1
gcd不为1则说明逆元不存在 ,若为1,则把x0调整到0~m-1的范围中即可
( ①:extgcd 目的 求 x ,y ; ②:逆元 目的 求 x )
一个数有逆元的充分必要条件是gcd(a,n)=1,如果gcd(a,n)>1,则不存在逆元
int exgcd(int a,int b,int &x,int &y)
{if(b==0) {x=1,y=0;return a;}int r = exgcd(b,a%b,x,y);int t = x;x = y;y = t - a/b*y;return r;
}
快速幂法
这个要运用 费马小定理 :
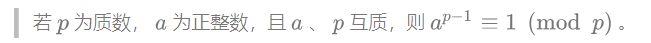
再看看推导过程:

由以上推导就可以通过求一个幂运算很简单的求出逆元辽。
上一个代码,具体功能就是求n和m的组合数mod1e9+7
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
const ll Mod=1e9 + 7;
ll fac[100010];//存阶乘
ll inv[100010];//存逆元 ll quick(ll a,int b)//快速幂算法
{ll ans=1;while(b){if(b&1)ans=(ans*a)%Mod;a=a*a%Mod;b>>=1;}return ans;
}void getfac()
{fac[0]=inv[0]=1;for(int i=1;i<=100000;i++){fac[i]=fac[i-1]*i%Mod;inv[i]=quick(fac[i],Mod-2); }
}ll getans(ll n,ll m)
{return fac[n]*inv[n-m]%Mod*inv[m]%Mod;
}int main()
{getfac();//初始化ll n,m;while(cin>>n>>m){ll ans=getans(n,m);cout<<ans<<endl;}
}
Lucas定理
对于大组合数取模,n,m不大于10 ^ 5的话,用逆元的方法,可以解决。对于n,m大于10 ^ 5的话,那么要求p<10 ^ 5,这样就是Lucas定理了,将n,m转化到10^5以内解。
Lucas定理是用来求 c(n,m) mod p,p为素数的值。
C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
也就是Lucas(n,m)%p=Lucas(n/p,m/p)*C(n%p,m%p)%p
求上式的时候,Lucas递归出口为m=0时返回1,原因是因为Lucas(a,0,q)=1;
模板:
#include <cstdio>
#include <iostream>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
#define maxn 100010
typedef long long LL;
LL m,n,p;
LL Pow(LL a,LL b,LL mod)
{ LL ans=1; while(b) { if(b&1)ans=(ans*a)%mod;a=a*a%mod;b>>=1;} return ans;
}
LL C(LL n,LL m)
{ if(n<m) return 0; LL ans=1; for(int i=1;i<=m;i++) { ans=ans*(((n-m+i)%p)*Pow(i,p-2,p)%p)%p; } return ans;
}
LL Lucas(LL n,LL m)
{ if(m==0) return 1; return (Lucas(n/p,m/p)*C(n%p,m%p))%p;
}
int main()
{ int t; scanf("%d",&t); while(t--) { scanf("%lld%lld%lld",&n,&m,&p); printf("%lld\n",Lucas(n,m)); } return 0;
}