基于卡方的独立性检验

article/2025/8/18 23:56:38

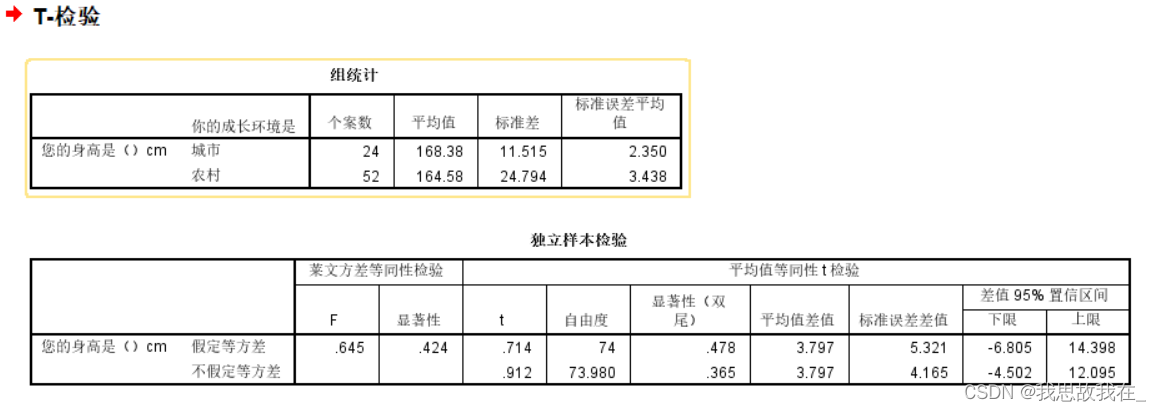
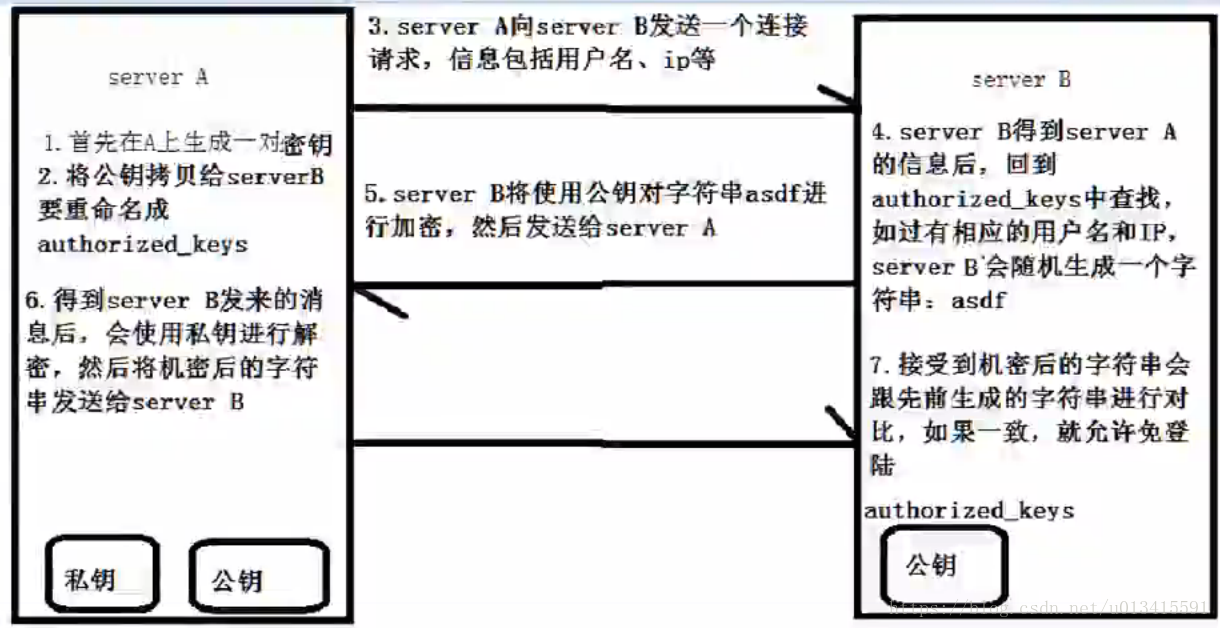
本文给出基于两种统计量的假设检验，来检验变量间是否独立--χ²与秩和。χ²越小说明越独立

假设检验

假设检验（Test of Hypothesis）又称为显著性检验（Test of Ststistical Significance）。

在抽样研究中，由于样本所来自的总体其参数是未知的，只能根据样本统计量对其所来自总体的参数进行估计，如果要比较两个或几个总体的参数是否相同，也只能分别从这些总体中抽取样本，根据这些样本的统计量作出统计推断，籍此比较总体参数是否相同。由于存在抽样误差，总体参数与样本统计量并不恰好相同，因此判断两个或多个总体参数是否相同是一件很困难的事情。

基本的解决方法是：根据问题的需要对所研究的总体作某种假设，记作H0；选取合适的统计量，这个统计量的选取要使得在假设H0成立时，其分布为已知；由实测的样本，计算出统计量的值，并根据预先给定的显著性水平进行检验，作出拒绝或接受假设H0的判断。常用的假设检验方法有u—检验法、t—检验法、χ²检验法、F—检验法，秩和检验等。

χ²独立性检

χ²检验是一种无参数的假设检验。

考虑这以一个问题：某地区有10000合法选民，现统计了男性和女性分别有多少人参加了投票。

		Men	Women
_____________________________
Voted		2792	3591
Didn't vote	1486	2131

问“性别”和“投票”是不是相互独立的？

下面就使用假设检验的方法解决这个问题。

我们假设H_0：性别和投票相互独立。备选假设H₁：性别与投票相关。

计算上表的行和与列和。

 OBSERVED TABLEMen	Women 	Total
_____________________________ |______
Voted		2792	3591  |	6383
Didn't vote	1486	2131  |	3617
_____________________________________
Total		4278	5722  |	10000

原始表中的数据用A_ij表示，行和用A_i·表示，列和用A_·j表示，全部元素的和用A_··表示。

投票的概率：

$p(v)=\frac{A_{1\cdot}}{A_{\cdot\cdot}}=0.6383$

选民为男性的概率：

$p(m)=\frac{A_{\cdot{1}}}{A_{\cdot\cdot}}=0.4278$

在H₀下，我们认为投票与性别无关，所以男性参加投票的概率为：

$p(m,v)=p(m)p(v)=0.2731$

这样可以算出男性投票的期望值：0.2731×10000=2731。于是就得到了下面这张“期望表”

	  EXPECTED TABLEMen	Women 	Total
_____________________________ |______
Voted		2731	3652  |	6383
Didn't vote	1547	2070  |	3617
_____________________________________
Total		4278	5722  |	10000

观察值与期望值的差值为误差。对于每一个观察值我们计算误差的平方与期望值的比值。

c11 = (2792-2731)^2/2731
c12 = (3591-3652)^2/3652
c21 = (1486-1547)^2/1547
c22 = (2131-2070)^2/2070

χ²=c11+c12+c21+c22=6.584283457

定义自由度为(rows-1)*(cols-1)，在我们的例子中自由度为1。

查表：

Degrees offreedom	99%  ...	10%	5%	1%
_____________________________________________________
1		0.00016		2.71	3.84	6.64
2 		0.020		4.60	5.99	9.21

由于χ²介于3.84和6.64之间，所以P值介于5%和1%之间，也就是说我们接收假设H₀的把握还不到5%，因此拒绝它。

最后给出CHI-Square独立检测的公式：

自由度 $DF=(r-1)*(c-1)$ ，r表示行数，c表示列数

期望值 $E_{r,c}=\frac{n_r*n_c}{n}$ ，n_r是行和，n_c是列和，n是所有元素的和

统计量 $\chi^2=\sum_{E_{r,c}\ne{0}}{\frac{(O_{r,c}-E_{r,c})^2}{E_{r,c}}}\qquad\cdots\cdots(3)$ ，O_r,c是观察值

由（3）式可以推出，对于一个2×2的contigency table，χ²统计量可以由（4）式来计算。

Variable 2	Data type 1	Data type 2	Totals
Category 1	a	b	a + b
Category 2	c	d	c + d
Total	a + c	b + d	a + b + c + d = N

$\chi^2=\frac{(a+b+c+d)(ad-bc)^2}{(a+b)(a+c)(c+d)(b+d)}\qquad\cdots\cdots(4)$

基于χ²的特征项选择

既然χ²统计量可以独立性检验，从独立性检验的对立面来考虑，χ²统计量也可以用来作相关性的度量。χ²越小说明变量之间越独立，χ²越大说明变量之间越相关。

	文档类别C_j	C_j的补集
词条w	a	b
w的补集	c	d

a表示词条w在类别C_j中出现的频数；b表示词条w在C_j以外的其他类别中出现的频数；c表示除w以外的其他词条在C_j中出现的频数；d表示除w以外的其他词条在除C_j外的类别中出现的频数。

利用公式（4）计算每个词条对于每种分类的χ²统计量，记为χ²(w,C_j)。 $ad-bc>0$ 说明词条与分类正相关； $ad-bc<0$ 说明词条与分类负相关。

则词条对整个语料库的记χ²值为

$\chi^2_{avg}=\sum{p(C_j)\chi^2(w,C_j)}\qquad\cdots\cdots(5)$

根据（5）式计算每个词条的平均χ²值，选最大的K个作为特征项。

秩和检验

秩和检验也是一种无参数的假设检验。它从两个未知分布的总体中独立、随机地抽取容量分别为n1、n2的样本，设n1<n2。然后把两个样本混合在一起进行排序，得到每个样本单位的秩次。当几个数据的大小相同秩次却不相同时，最终的秩次取其算术平均。

数据：	5	6	6	7	7	8	8	9	10	10	11
秩号：	1	2.5	2.5	4.5	4.5	6.5	6.5	8	9.5	9.5	11

红颜色的数据来自一个总体，黑颜色的来自另一个总体。n1=5,n2=6。

原假设：两个总体服从相同的分布。

备选假设：两个总体服从不同的分布。

总体Ⅰ的秩和 T=2.5+4.5+6.5+6.5+9.5=29.5

取显著水平α=0.05，进行双侧检验，查“秩和检验表”，n1=5，n2=6，得临界值T1(α)=20，T2(α )=40。

20<29.5<40，样本落入接受域，所以接受原假设。