算法基础|avl树实现思路、左旋与右旋的理解

第一次学习avl树，感觉有点复杂，花了大半天的时间算是理解了一些皮毛。

基础

avl树是什么？

什么时候会自动开始调整呢？

如何进行自动平衡操作？

旋转是什么？

什么时候旋转两次？

总实现

基础

avl树是什么？

avl树是基于BST（二叉搜索树、二叉排序树）的一种数据结构，算是BST缺点的一种解决方案，特点是会自动调整树的高度，使得整个树中所结点的左右子树的高度差<=1。

如何得到左右子树的高度呢？

从叶子结点开始算起，叶子结点高度为0；如果一个结点，不是叶子结点，那么该节点的高度取决于左右子树中高度最高者+1，即

结点高度=max（左子树高度，右子树高度）+1

这样一来，事情就变得简单了，我们只需要在结点类中赋予相关的算法，即可实现获得结点高度的功能

大致设计如下：

（两种写法，思路是一致的）
    // 返回 以该结点为根结点的树的高度 ，为计算平衡因子而设计
//语法糖写法public int height() {//left == null ? 0 : left.height()，// 意思是左子树是否为空，如果左子树为空的话，说明左子树没有高度，赋予高度0，// 如果左子树不为空，那么递归下去，直到空为止，返回值会自己不断地增长，// 右边同理.int max = Math.max(left == null ? 0 : left.height(),right == null ? 0 : right.height());return max + 1;}//非语法糖写法public int height() {if (left == null) {if (right == null) {return 1;} else return right.height() + 1;} else {if (right == null) {return left.height() + 1;}return Math.max(right.height(), left.height()) + 1;}}

什么时候会自动开始调整呢？

答：树中存在一个结点，该结点的左右子树高度差>1时。

好像是一句废话，接着往下推导，什么时候会造成左右子树高度差>1？

答曰：进行增加操作or删除操作时。

因此，在进行增删操作时，需要进行自动平衡的操作。

如何进行自动平衡操作？

根据具体的情况，进行不同的操作。

根据各种算法教程所述，一共有四种破坏平衡的情况，对应着四种操作。

这四种情况及应对的操作分别是：

1.Right Rotation (RR)

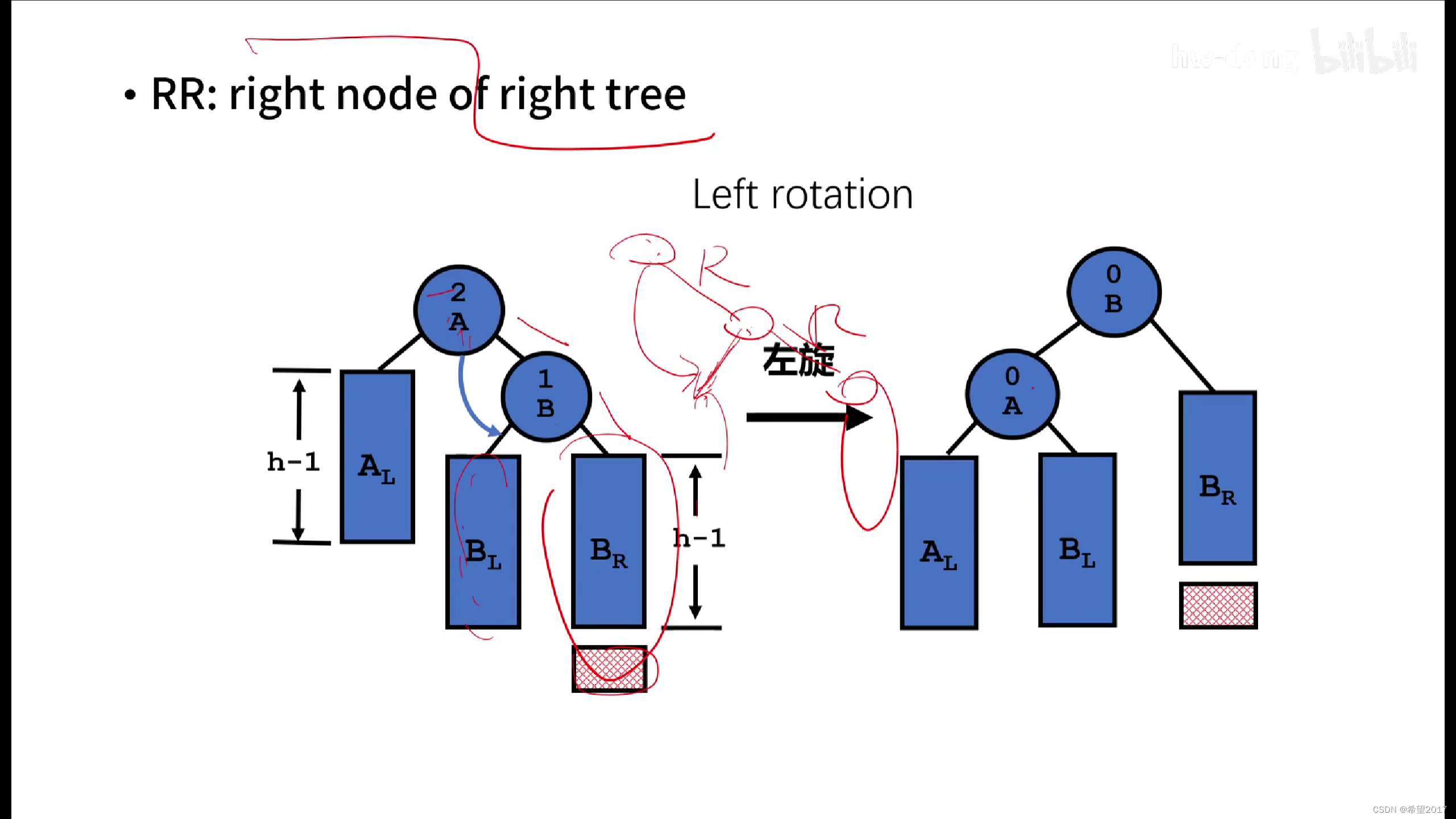
进行RR操作的情况：造成树失衡的原因源于右子结点的右子树（right tree of right node）。（不过说是右子树的右子结点也没什么毛病）

2.Left Rotation (LL)

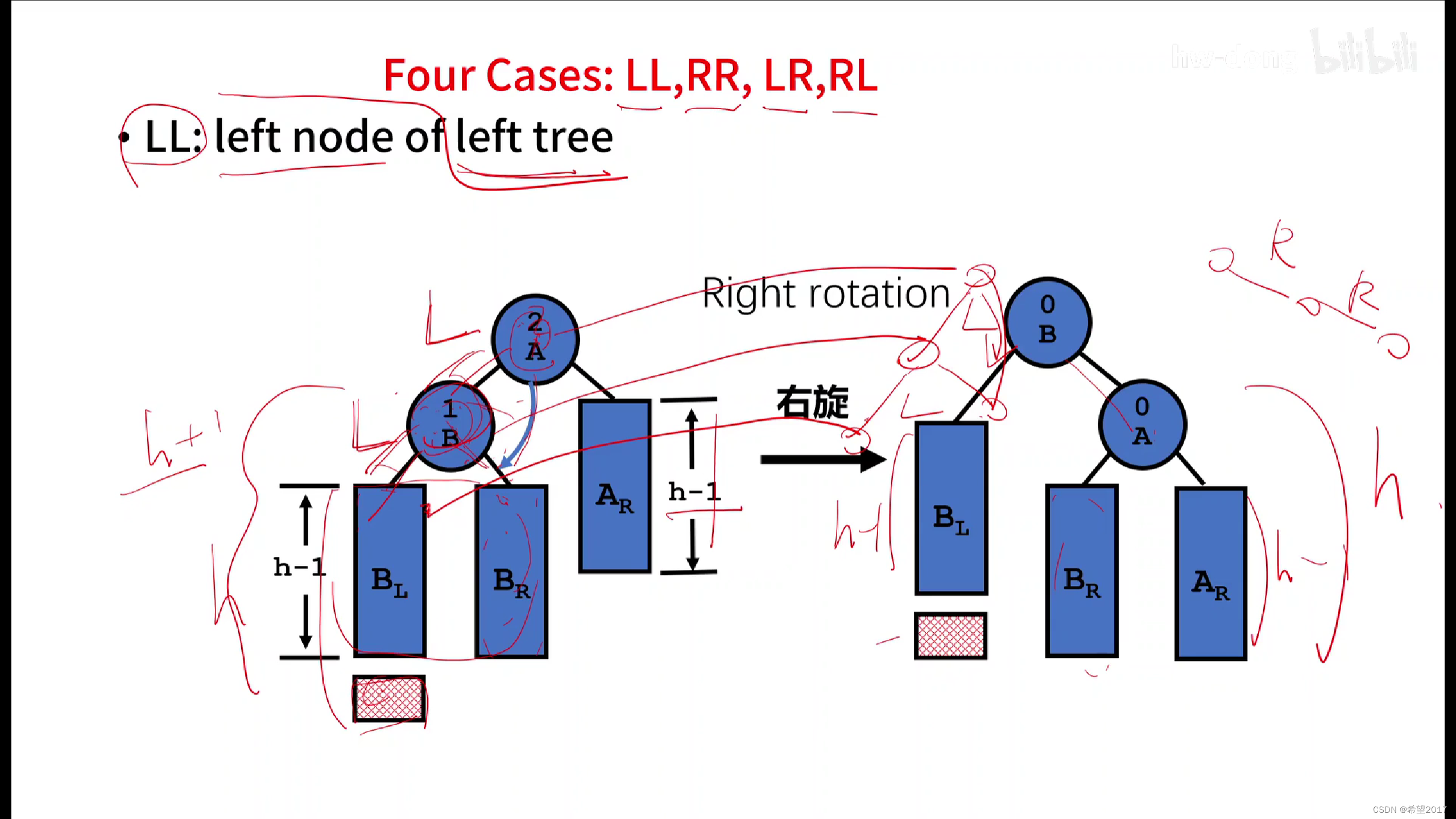
同理；

3.Left-Right Rotation (LR) or "Double left"

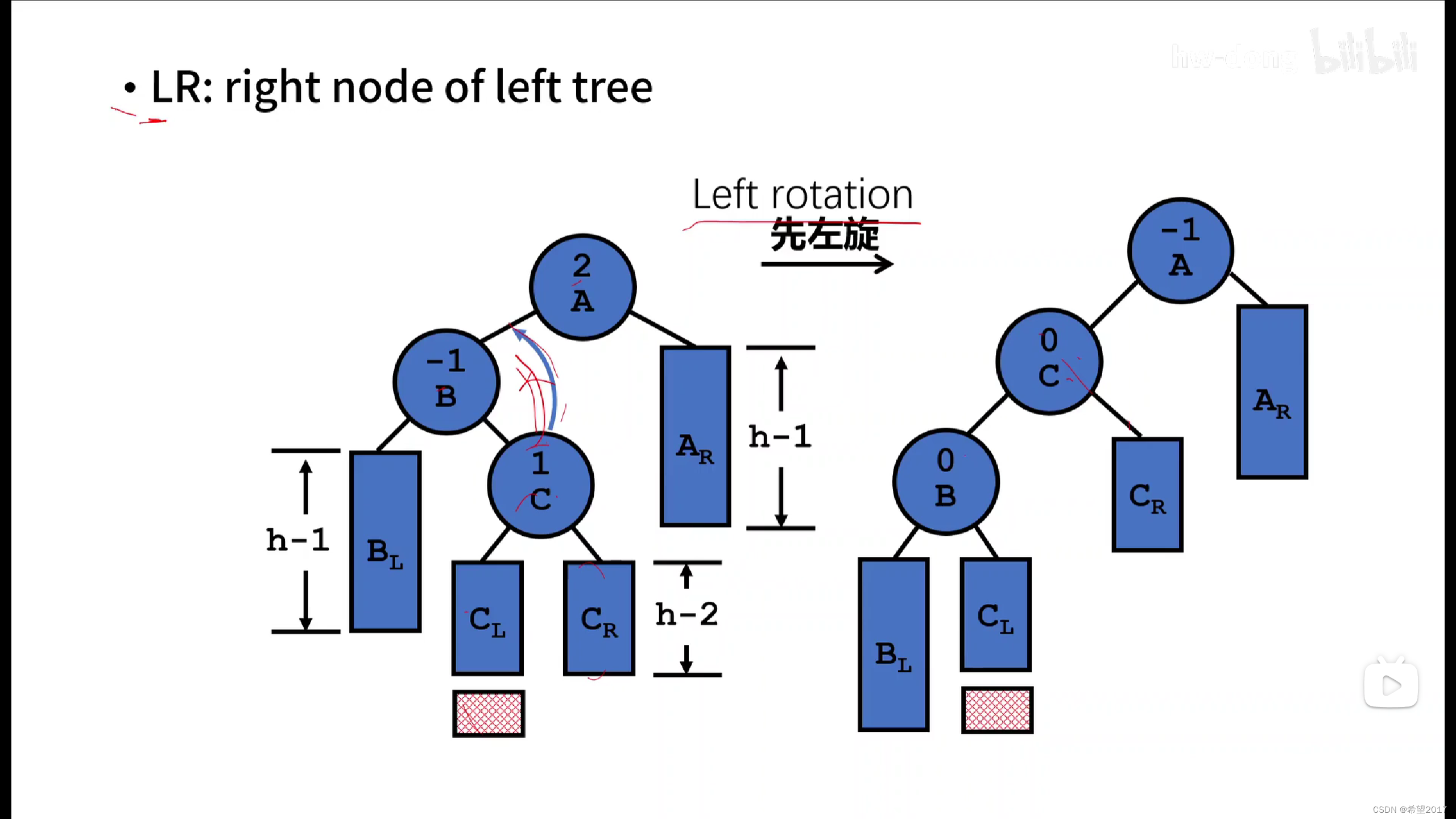
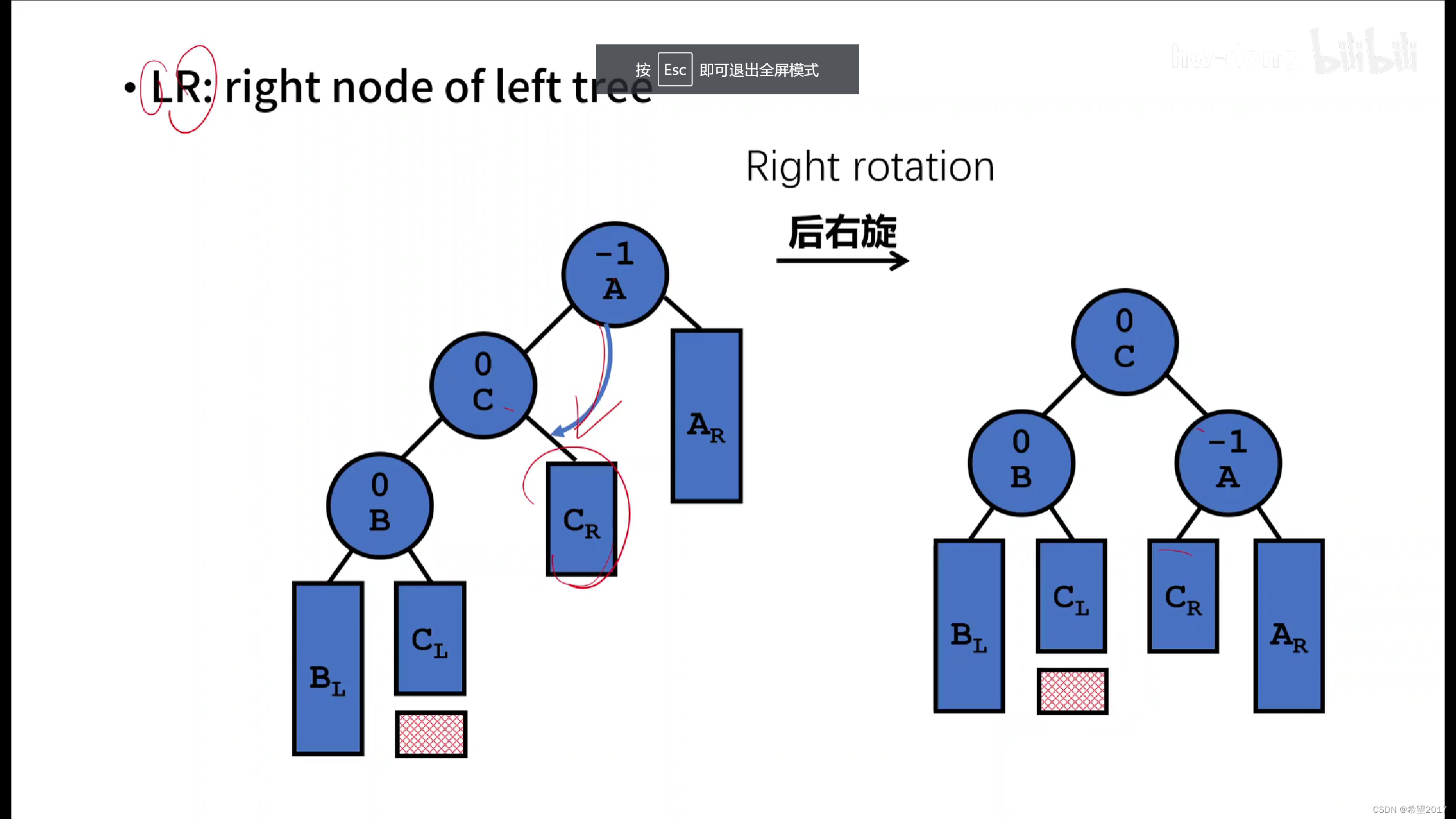
进行LR操作的情况：造成树失衡的原因源于左子节点的右子树（right node of left tree）

(后面会详细说明)

4.Right-Left Rotiation (RL) or "Double right"

类似于3.

旋转是什么？

旋转是改变子树结构的行为，通常说的进行左旋or右旋，指的是改变某棵树的某些结点的父子关系，从外观上看，就好像把某些结点向左or向右的进行了旋转。旋转得当可以减少树的高度（可以将高度-1）。

树的旋转是不太好理解的，因为旋转这个动作并不是单一结点的变化，而是许多结点都发生了变化。

旋转并不是某一个结点的事情，而是一棵树的事情，在外观的图上，有时候可以理解为根结点向下旋转，有时候也可以理解为根结点的子节点向上旋转，怎么方便怎么来。

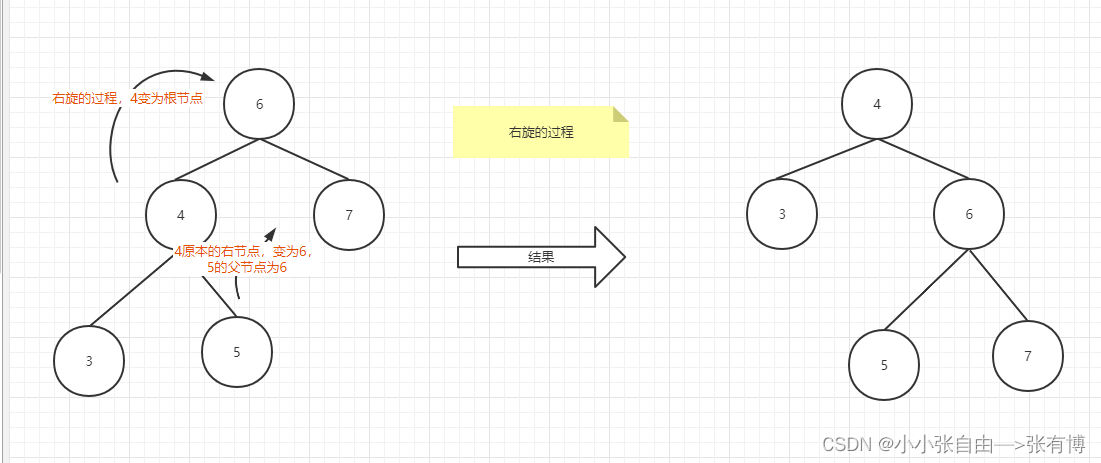
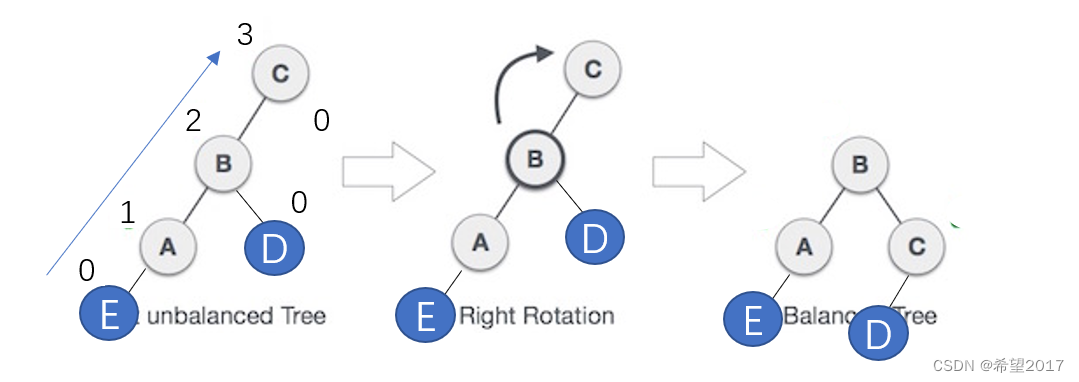
下图为为失衡树的平衡过程，即右旋过程，从外观上看也就是把C结点向右旋转的操作（或者B结点，都行，只要方便理解或者实现）：

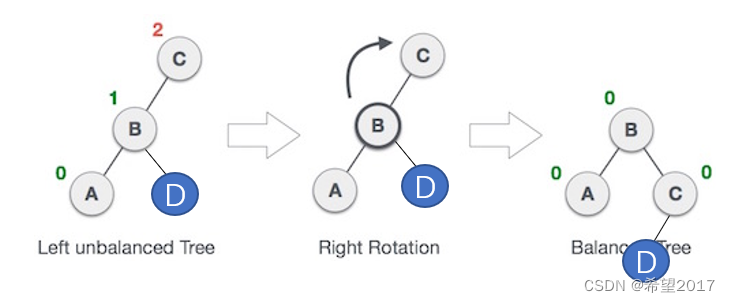
图右旋操作（最后一步高度标志有错误）

可以看到C结点右旋后，原左子结点成为了父结点，B结点由于要多一个子结点C，所以原来的右子结点D就不能要了，也就是D结点需要从B中脱离，为了满足BST的特点，D结点需要成为C结点的左子结点。这样一来，C的右旋操作就完成了。

Java实现代码如下：（我把旋转的方法写到结点类里面了，写到其他地方也可以）

    //右旋转private void rightRotate() {//创建新的结点，值为当前根值Node newNode = new Node(value);//给新结点，即新C结点左右孩子结点newNode.right = right;newNode.left = left.right;//将原根结点左结点赋予值与引用，成为新的根结点，//即C成为新的B，原B无引用，会被自动回首value = left.value;left = left.left;right = newNode;}

旋转的代码实现有很多种方式，既可以写在结点里面，也可以写在树里面，怎么实现并无统一标准，只要旋转后满足高度要求就好了。

什么时候旋转两次？

当导致平衡因子不满足条件的高度的来源不是同一侧时，需要旋转两次。

图对失衡子树进行左旋操作

这句话有点抽象，首先来介绍一下什么叫做平衡因子。

平衡因子：某个结点的左子树的高度减去右子树的高度得到的差值。

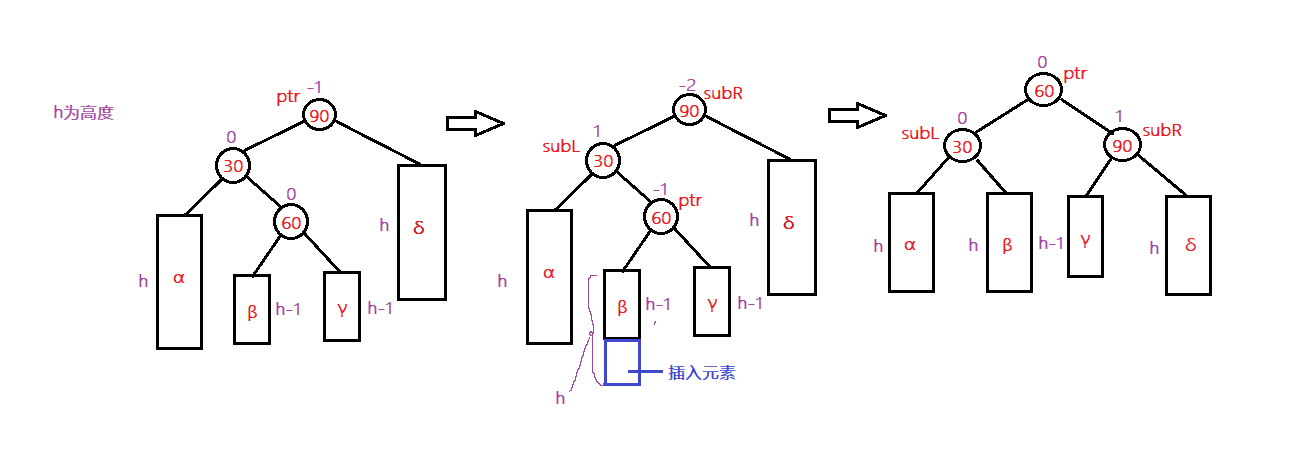
直接上图：

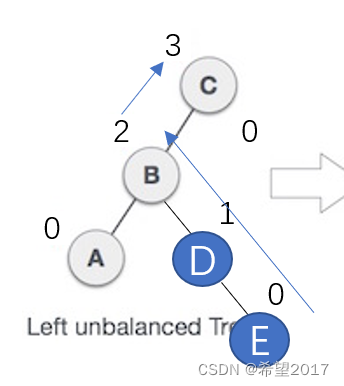
这个图上，每个结点上边都标注了一个数字，数字代表该结点的高度。结点左右子树的高度差就是平衡因子，可以看出，C结点的平衡因子为2，并不满足AVL树的要求，因此需要旋转。那么如何旋转呢，看看是谁导致了平衡因子被破坏掉了，哦，原来是B结点的高度太高了，那么又是谁导致B结点的高度为2呢？一看，原来是D结点的高度为1，导致了B结点的高度为2。好了，到此为止，总结一下，我们发现C的平衡因子不满足条件，原因源自B结点，而B结点的高度源自D结点，D结点并不是像其父结点B结点，是一个左子节点，而是右子节点，那么此时，就需要旋转2次。

下图这种，就不需要旋转2次，因为导致不平衡的结点都在一侧：

根据以上内容，Java代码实现如下：

        //当添加完一个结点后，如果: (右子树的高度-左子树的高度) > 1 , 左旋转if (rightHeight() - leftHeight() > 1) {//如果它的右子树的左子树的高度大于它的右子树的右子树的高度if (right != null && right.leftHeight() > right.rightHeight()) {//先对右子结点进行右旋转right.rightRotate();//然后在对当前结点进行左旋转leftRotate(); //左旋转..} else {//直接进行左旋转即可leftRotate();}return; //代码规范性的体现}//当添加完一个结点后，如果 (左子树的高度 - 右子树的高度) > 1, 右旋转if (leftHeight() - rightHeight() > 1) {//如果它的左子树的右子树高度大于它的左子树的高度if (left != null && left.rightHeight() > left.leftHeight()) {//先对当前结点的左结点(左子树)->左旋转left.leftRotate();//再对当前结点进行右旋转rightRotate();} else {//直接进行右旋转即可rightRotate();}}

总实现

public class AVLTree_1 {public static void main(String[] args) {int[] arr = {1, 20, 2, 19, 3};//创建一个 AVLTree对象AvlTree avlTree = new AvlTree();//添加结点for (int i = 0; i < arr.length; i++) {avlTree.add(arr[i]);}System.out.println("树的高度=" + avlTree.root.height()); //5System.out.println("树的高度=" + avlTree.root.right.height()); //5System.out.println("树的高度=" + avlTree.root.left.height()); //5avlTree.infixOrder();}
}class AvlTree {Node root;public void infixOrder() {if (root != null) {root.infixOrder();} else {System.out.println("二叉排序树为空，不能遍历");}}public void add(int val) {if (root == null) {root = new Node(val);} else {add(root, val);}}private void add(Node node, int val) {//命中if (node == null) {return;}if (val > node.val) {if (node.right == null) {node.right = new Node(val);} else add(node.right, val);} else {if (node.left == null) {node.left = new Node(val);} else add(node.left, val);}checkHeight(node);}private void checkHeight(Node node){//判断树高//如果左边比右边高，右旋if (leftHeight(node.left) - rightHeight(node.right) > 1) {//如果左子结点的右子树比左子树高，先把该结点左旋if (node.right != null && rightHeight(node.left.right) - leftHeight(node.left.left) > 1) {node.left.leftRotate();} else {node.rightRotate();}} else if (rightHeight(node.right) - leftHeight(node.left) > 1) {//如果右边比左边高，左旋if (node.left != null && leftHeight(node.left.right) > rightHeight(node.left.left)) {node.right.rightRotate();} else {node.leftRotate();}}}private int rightHeight(Node right) {if (right == null) {return 0;} else return right.height();}private int leftHeight(Node left) {if (left == null) {return 0;} else return left.height();}public void del() {}}class Node {int val;Node left;Node right;@Overridepublic String toString() {return "Node{" +"val=" + val +'}';}public Node(int val) {this.val = val;}public int height() {//非语法糖写法
//        if (left == null) {
//            if (right == null) {
//                return 1;
//            } else return right.height() + 1;
//        } else {
//            if (right == null) {
//                return left.height() + 1;
//            }
//            return Math.max(right.height(), left.height()) + 1;
//        }//语法糖写法return Math.max(left == null ? 0 : left.height(),right == null ? 0 : right.height()) + 1;}public void leftRotate() {//左旋是因为该结点左右子树高度差大于1了//要将该结点作为右子结点的子节点，把右子结点当做根结点，其他结点顺序调整//如果从该结点的父结点出发，将该结点设置成该结点的右子结点，需要拿到父结点的指针//这是一件麻烦的事情，因此直接将该结点的值设置成该结点的右子结点，这样是很方便的Node newNode = new Node(val);newNode.right = right.left;newNode.left = left;val = right.val;left = newNode;right = right.right;}public void rightRotate() {//创建新的结点，值为当前根值Node newNode = new Node(val);//给新结点，即新C结点左右孩子结点newNode.right = right;newNode.left = left.right;//将原根结点左结点赋予值与引用，成为新的根结点，即C成为新的B，原B无引用，会被自动回收val = left.val;left = left.left;right = newNode;}public void infixOrder() {if (this.left != null) {this.left.infixOrder();}System.out.println(this);if (this.right != null) {this.right.infixOrder();}}
}

引用：

详解 AVL 树（基础篇） - 知乎

【尚硅谷】数据结构与算法（Java数据结构与算法）_哔哩哔哩_bilibili

2021年最好懂的红黑树_哔哩哔哩_bilibili

Microsoft Word - AVLTreeTutorial.rtf (ufl.edu)

AVL Tree – Introduction to LL, RR, LR, RL rotations and its implementation | Codingeek